
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 30 minutes | Coding time: 6 minutes
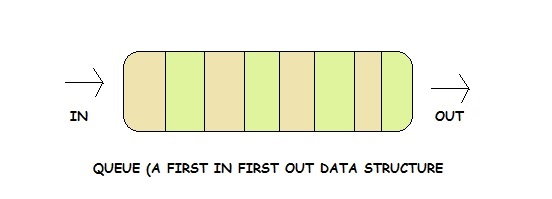
Queue is a linear data structure that can be used to store data in an order by imposing rules on data insertion and deletion. It is a simple data structure but has found immense use and can be implemented using arrays and linked lists.
In our everyday life we see many types of queues. People standing in queue to buying stuff, ants walking in queue. Similarly, in computer science, queue is linear Data structure in which data stored and manipulated in queue manner and hence, this data structure has been influenced by real life ordering.

Definition
A queue is defined over an array or linked list by two data elements/ identifiers:
- rear
- front
A queue is an ordered list in which insertions are done at one end (rear) and deletions are done at other end (front). The first element to be inserted is the first one to be deleted. Hence, it is called First in First out (FIFO) or Last in Last out (LILO) list.
Queues can be implemented by using:
- arrays
- linked lists
- stack (which in turn uses array or linked lists)
In this article We will implement Queue using array. Queues maintain two data pointers:
- FRONT
- REAR
to know first inserted element and last inserted element. Queue is very simple data structure ,you only have to manipulate FRONT and REAR to get Queue property.
Basic Operations
Following are basic operations of Queue:
- EnQueue(): Inserts an element at the end of the queue
- DeQueue():It will Remove and return the front element of the queue
In addition to the above operations, an implementation of queue may provide the following commonly used utilities as well:
- Front(): Returns the element at the front without removing it.
- QueueSize(): Returns the number of elements stored in the queue.
- display():display elements of queue
EnQueue
Pseudocode:
Step 1: IF REAR = MAX-1
Write OVERFLOW
Goto step 4
[END OF IF]
Step 2: IF FRONT = -1 and REAR = -1
SET FRONT = REAR =0
ELSE
SET REAR = REAR + 1
[END OF IF]
Step 3: SET QUEUE[REAR] = NUM
Step 4: EXIT
Example
Let's see implementation of Queue and its operations,with example
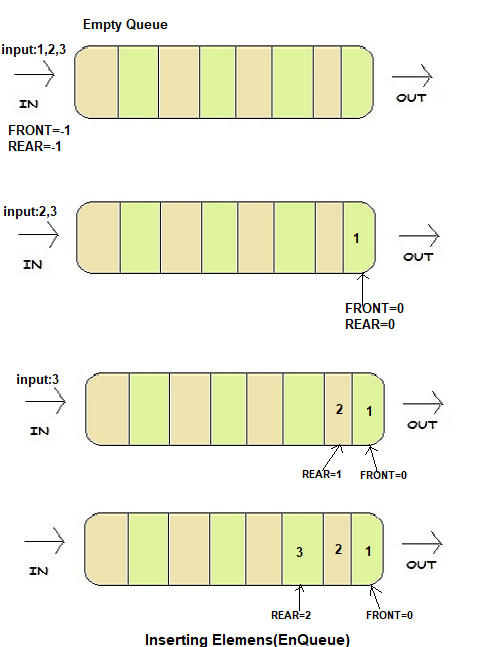
let say we have a queue of maximum capacity 5. Initially FRONT=-1,REAR=-1 because queue is empty.
Now we have data input 1,2,3.
On first insertion, FRONT and REAR both increment its value, because at first both will point to the same position 0 (We are using 0 based indexing). Afterwards only REAR will increment its value to point the last element inserted but before inserting element at REAR pointed position we have to check the overflow condition ,We can only insert element up to the Maxcapacity-1 therefor after REAR=Maxcapacity-1 we can't increment value of REAR .So after inserting 1,2,3 FRONT=0 REAR=2.
DeQueue
Deleting an element from Queue.
In deletion,we are not deleting element we are just restricting their access.
Step 1: IF FRONT = -1 OR FRONT > REAR
Write UNDERFLOW
ELSE
SET VAL = QUEUE[FRONT]
SET FRONT = FRONT + 1
[END OF IF]
Step 2: EXIT
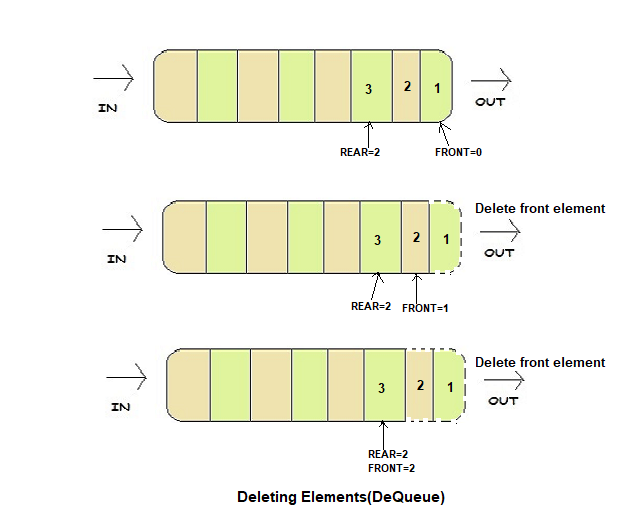
Now we want to delete elements of a queue,as we know Queue follows First in First out,So our first element 1 will be deleted first.To delete first element ,we will simply increment value of FRONT by 1 . Now first elements will be the element pointed by FRONT=1.Afterward on every deletion we have to increment FRONT by 1. Before incrementing FRONT we have to check Underflow condition,if queue is empty and user perform Dequeue operation there will not be any element to delete or suppose you have inserted 3 elements and you deleted all that element,now user perform Dequeue operation at this time also there will not be any element to delete.
This both are the main Operations of queue. According to our requirement we can implement other operations like display, delete, size of queue and others
Complexity
- Time complexity of enqueue and dequeue operations is O(1), Because there is no loop in any operation.
- Space complexity is O(n) where n is number of elements.
Implementation
#include<iostream>
#define MAX 10
using namespace std;
int REAR = -1,FRONT = -1;
int Queue[MAX];
void EnQueue();
int DeQueue();
int Front();
void display();
int QueueSize();
int main()
{
int choice,num;
while(1)
{
cout<<"\n1.EnQueue\n2.DeQueue\n3.Display\n4.Front Element\n5.Size of Queue\n6.Exit\nEnter Choice:";
cin>>choice;
switch(choice)
{
case 1:
EnQueue();
break;
case 2:
num=DeQueue();
if(num!=-1)
cout<<"Number deleted is "<<num;
break;
case 3:
display();
break;
case 4:
num=Front();
if(num != -1)
cout<<"Front element is "<<num;
break;
case 5:
num=QueueSize();
if(num == 0)
cout<<"Queue is empty\n";
else
cout<<"Size of Queue is "<<num;
break;
case 6:
return 0;
}
}
}
void EnQueue()
{
int num;
cout<<"\n Enter the number to be inserted in the queue : ";
cin>>num;
if(REAR == MAX-1)
cout<<"\n OVERFLOW";
else if(FRONT == -1 && REAR == -1)
FRONT = REAR = 0;
else
REAR++;
Queue[REAR] = num;
}
int DeQueue()
{
int val;
if(FRONT == -1 || FRONT>REAR)
{
cout<<"\n UNDERFLOW";
return -1;
}
else
{
val = Queue[FRONT];
FRONT++;
if(FRONT > REAR)
FRONT = REAR = -1;
return val;
}
}
int Front()
{
if(FRONT==-1 || FRONT>REAR)
{
cout<<"\n QUEUE IS EMPTY";
return -1;
}
else
{
return Queue[FRONT];
}
}
void display()
{
int i;
cout<<endl;
if(FRONT == -1 || FRONT > REAR)
cout<<"\n QUEUE IS EMPTY";
else
{
for(i = FRONT;i <= REAR;i++)
cout<<Queue[i]<<" ";
}
}
int QueueSize()
{
if( FRONT==-1 && REAR==-1)
return 0;
else
return (REAR-FRONT+1);
}
Applications
- In scheduling processes and threads in Operating system.
- In Printer, Files will be in queue to be printed.
- When data is transferred asynchronously (data not necessarily received at same rate as sent) between two processes. Examples include IO Buffers, pipes, file IO and others.
