Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 30 minutes | Coding time: 10 minutes
Bucket sort is a comparison sort algorithm that works by distributing the elements of an array into a number of buckets and then each bucket is sorted individually using a separate sorting algorithm or by applying the bucket sort algorithm recursively.This algorithm is mainly useful when the input is uniformly distributed over a range.
Algorithm
- Create an empty array of size n(n empty buckets).
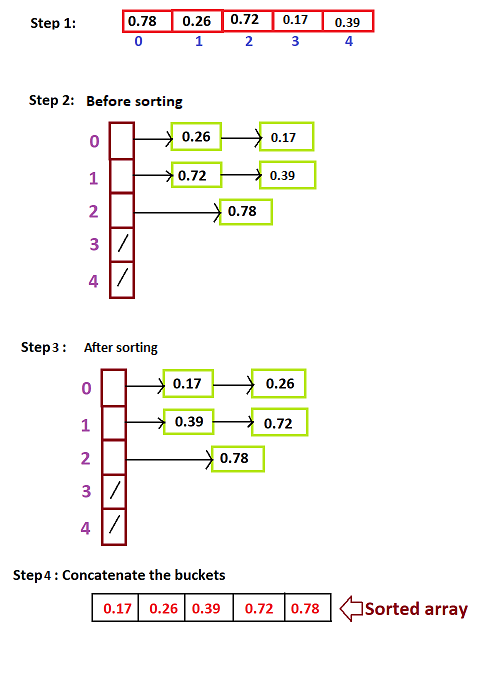
- Loop through the original array and put each array element in a “bucket”.
- Sort each of the non-empty buckets using insertion sort.
- Visit the buckets in order and put all elements back into the original array
Example
Let's take an array A[]={0.78,0.26,0.72,0.17,0.39}. Total number of elements are n=10. So we need to create 5 buckets.
maximum element(max)=0.78
Using the formula: bi = (n)*arr[i]/(max+1), we find out bucket index of each element of the array A[].
For eg: bucket index of 0th element is bi= floor((5)(0.78)/(0.78+1))= 2
Similarly,bucket index of 1st element is bi=0
bucket index of 2nd element is bi=1
bucket index of 3rd element is bi=0
bucket index of 4th element is bi=1
Now, since buckets have been created we need to concatenate all the buckets in the order to get the sorted array.
Pseudocode
Step 1: function bucketSort(array, n) is
Step 1: buckets ← new array of n empty lists
Step 2: M ← the maximum key value in the array
Step 3: for i = 1 to length(array) do
insert array[i] into buckets[floor(array[i] / M * n)]
Step 4: for i = 1 to n do
sort(buckets[i])
Step 5: return the concatenation of buckets[1], ...., buckets[k]
Complexity
Worst case time complexity:Θ(n^2)
Average case time complexity:Θ(n+k)
Best case time complexity:Θ(n+k)
Space complexity:Θ(n+k)
where n is the number of elements to be sorted and k is the number of buckets
For an upper bound on the worst-case cost, it's sufficient to show that it can't be worse. Assuming that insertion sort takes ≤cn2 steps on n elements, consider the sum
it is an upper bound on the cost of sorting all the buckets. For an upper bound on the worst case for bucket sort, maximize this function subject to ∑|Bi|=n (and add the remaining cost, which is O(n) for all inputs).
For a lower bound on the worst-case cost, we have to find an infinite class of actual inputs and show that their cost behaves as claimed. [0,…,0] serves to show an Ω(n2) lower bound.
Implementation
- C++
C++
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
float findMax(float A[], int n)
{
if (n == 1)
return A[0];
return max(A[n-1], findMax(A, n-1));
}
void bucketSort(float arr[], int n)
{
float max=findMax(arr,n);
vector<float> b[n];
// 2) Put array elements in different buckets
for (int i=0; i<n; i++)
{
int bi = n*arr[i]/(max+1); // Index in bucket
b[bi].push_back(arr[i]);
}
// 3) Sort individual buckets
for (int i=0; i<n; i++)
sort(b[i].begin(), b[i].end());
// 4) Concatenate all buckets into arr[]
int index = 0;
for (int i = 0; i < n; i++)
for (int j = 0; j < b[i].size(); j++)
arr[index++] = b[i][j];
}
int main()
{
int n;
float arr[n];
for(int i=0;i<n;i++)
cin>>arr[i];
bucketSort(arr, n);
cout << "Sorted array is \n";
for (int i=0; i<n; i++)
cout << arr[i] << " ";
return 0;
}Applications
Constructing Histograms
One common computation in data visualization and analysis is computing a histogram. For example, n students might be assigned integer scores in some range, such as 0 to 100, and are then placed into ranges or “buckets” based on these scores.