
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 20 minutes | Coding time: 7 minutes
Counting sort is an algorithm for sorting integers in linear time. It can perform better than other efficient algorithms like Quick Sort, if the range of the input data is very small compared to the number of input data. It is a stable, non-comparison and non-recursive based sorting.
It takes in a range of integers to be sorted. It uses the range of the integers (for example, the range of integers between 0–100), and counts the number of times each unique number appears in the unsorted input. It works by counting the number of objects having distinct key values (kind of hashing). Then doing some arithmetic to calculate the position of each object in the output sequence.
In Counting sort, the frequencies of distinct elements of the array to be sorted is counted and stored in an auxiliary array, by mapping its value as an index of the auxiliary array.
Is counting sort a comparison based sorting algorithm?
Algorithm
Let's assume that, array A of size N needs to be sorted.
- Step 1: Initialize the auxilliary array Aux[] as 0.
(Note: The size of this array should be ≥max(A[])) - Step 2: Traverse array A and store the count of occurrence of each element in the appropriate index of the Aux array, which means, execute Aux[A[i]]++ for each i, where i ranges from [0,N−1].
- Step 3: Initialize the empty array sortedA[]
- Step 4: Traverse array Aux and copy i into sortedA for Aux[i] number of times where 0≤ i ≤max(A[]).
Example
The operation of COUNTING - SORT on an input array A[1...8], where each element of A is a non-negative integer no larger than k = 5.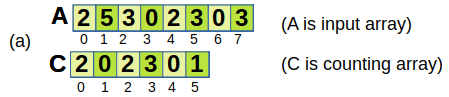
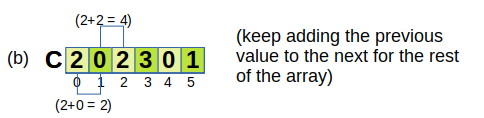

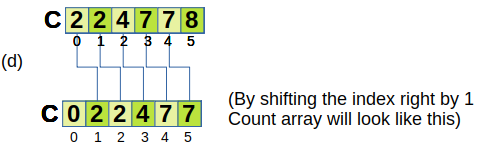
Now taking new array B of same length as of original. Put number at the value at that index and then increament the value at the index of the count array.

Note:-
The array A can be sorted by using this algorithm only if the maximum value in array A is less than the maximum size of the array Aux. Usually, it is possible to allocate memory up to the order of a million (10^6). If the maximum value of A exceeds the maximum memory- allocation size, it is recommended that you do not use this algorithm. Use either the quick sort or merge sort algorithm.
Implementation
Assume that the maximum element that can be in the array is K.
Now take an Aux[] array of size K + 1.
A[] = Array to be sorted.
sortedA[] = Sorted version of A[].
- C++
C++
// C++ Program for counting sort
#include <iostream>
Using namespace std;
void counting_sort(int A[], int Aux[], int sortedA[], int N) {
// First, find the maximum value in A[]
int K = 0;
for(int i=0; i<N; i++) {
K = max(K, A[i]);
}
// Initialize the elements of Aux[] with 0
for(int i=0 ; i<=K; i++) {
Aux[i] = 0;
}
// Store the frequencies of each distinct element of A[],
// by mapping its value as the index of Aux[] array
for(int i=0; i<N; i++) {
Aux[A[i]]++;
}
int j = 0;
for(int i=0; i<=K; i++) {
int tmp = Aux[i];
// Aux stores which element occurs how many times,
// Add i in sortedA[] according to the number of times i occured in A[]
while(tmp--) {
//cout << Aux[i] << endl;
sortedA[j] = i;
j++;
}
}
}
Say A={5,2,9,5,2,3,5}.
Aux will be of the size 9 + 1 i.e. 10
Aux={0,0,2,1,0,3,0,0,0,2}.
Notice that Aux[2] = 2 which represents the number of occurrences of 2 in A[]. Similarly Aux[5] = 3 which represents the number occurrences of 5 in A[].
After applying the counting sort algorithm, sortedA[] will be {2,2,3,5,5,5,9}
Complexity
The array A is traversed in O(N) time and the resulting sorted array is also computed in O(N) time. Aux[] is traversed in O(K) time. Therefore, the overall time complexity of counting sort algorithm is O(N+K).
Worst case time complexity:Θ(N+K)
Average case time complexity:Θ(N+K)
Best case time complexity:O(N+K)
Space complexity:O(N+K)
where N is the range of elements and K is the number of buckets
Important Points
- Counting sort works best if the range of the input integers to be sorted is less than the number of items to be sorted
- It is a stable, non-comparison and non-recursive based sorting.
- It assumes that the range of input is known
- It is often used as a sub-routine to another sorting algorithm like radix sort
- Counting sort uses a partial hashing to count the occurrence of the data object in O(1) time
- Counting sort can be extended to work for negative inputs as well
