Heap Sort

Reading time: 25 minutes | Coding time: 10 minutes

Algorithm

Consider that we are using Max heap as the underlying structure for heapsort.

Max heap is a binary heap such as the root node is larger than all nodes that are a part of its left and right sub trees which are in turn max heap. An instant insight is that the root node of a max heap is the maximum element of the set of elements

Hence, the first step is to create a Max heap from the given set of N elements. This step takes O(N) time complexity

Second step is to remove the root element which is the largest element and replace it with the bottom most node which is a left. Hence, the set of elements has now N-1 elements and the tree is not a max heap. To make it a Max heap again, we need to check each node and swap the parent and child nodes accordingly. This step takes O(log N) time complexity.

The above step is repeated N-1 times till we are left with only one element.

Hence, the overall complexity is O(N log N) and it uses are fundamental property of binary heaps to sort a dataset.

Complexity

• Worst case time complexity: Θ(nlogn)
• Average case time complexity: Θ(nlogn)
• Best case time complexity: Θ(nlogn)
• Space complexity: Θ(1)

Pseudocode

procedure heapsort(array, n):
     // Step 1: creating the initial Max heap
     for i = n/2 - 1 to 0 do:
         heapify(array, n, i)
     // Step 2: Removing one element and maintaining the heap property
     for i = n-1 to 0 do:
         swap(array[0], array[i])
         heapify(array, i, 0) 
         
procedure heapify(array, n, i)
    // initialize largest as root and get left and right nodes
    int largest = i;
    int left_node = 2*i + 1;
    int right_node = 2*i + 2;
    // Check if left node exists and is larger than root. If yes, change it
    if(left_node < n && arr[left_node] > arr[largest])
        largest = left_node;
    // Check if right node exists and is larger than root. If yes, change it
    if(right_node < n && arr[right_node] > arr[largest])
        largest = right_node;
    // change root, if needed
    if(largest != i)
        swap(arr[i], arr[largest]);
        heapify(arr, n, largest);

Example

Dataset: 4 10 3 5 1

We create a heap which we covert to a Max Heap in O(N) time complexity

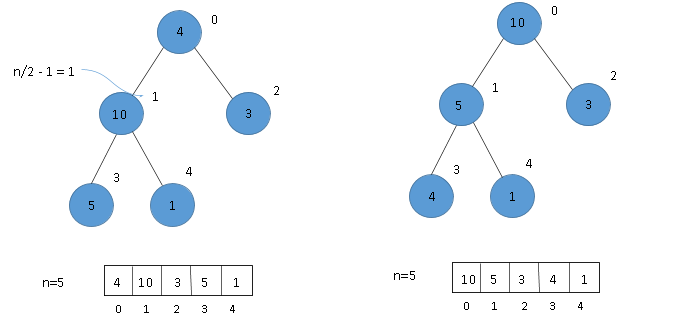
(1) Building a Heap tree. (2) Creating a Max heap in which child nodes are less than root node.

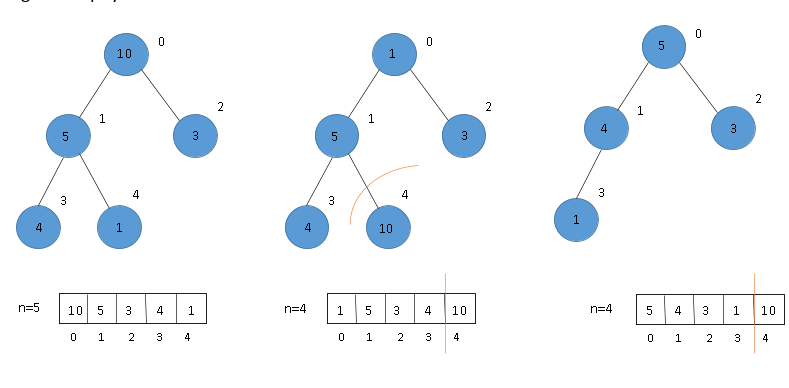
(2) Swap 1st and last nodes (10 and 1) and build heap again. (3) Exclude last node and heapify again.

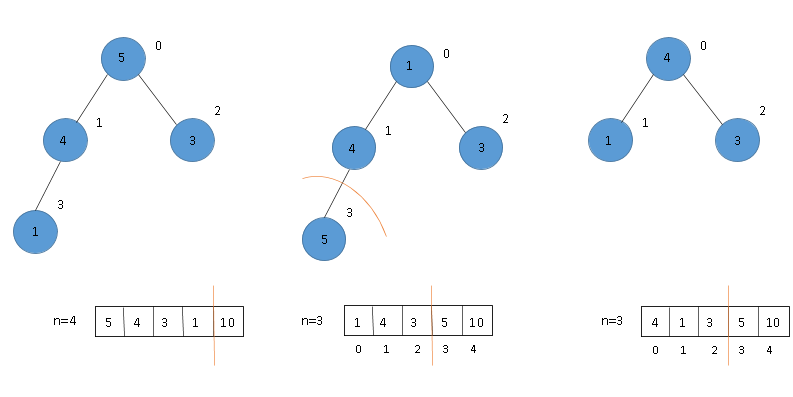
(2) Swap 1st and last node (5 and 1) and build heap. (3) Exclude last node and heapify.

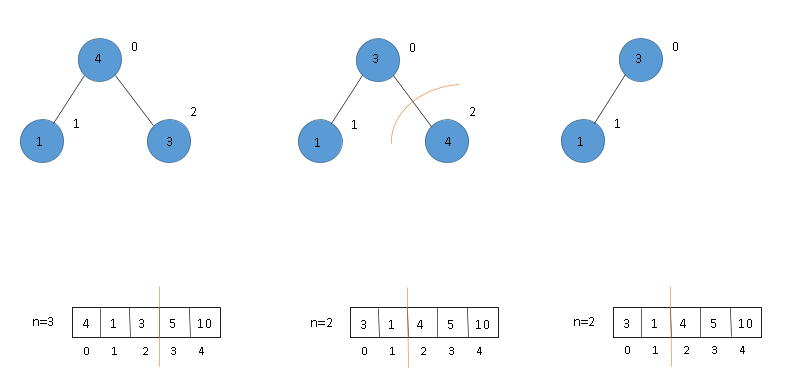
(2) Swap 1st and last node (4 and 3) and build heap. (3) Exclude last node and heapify.

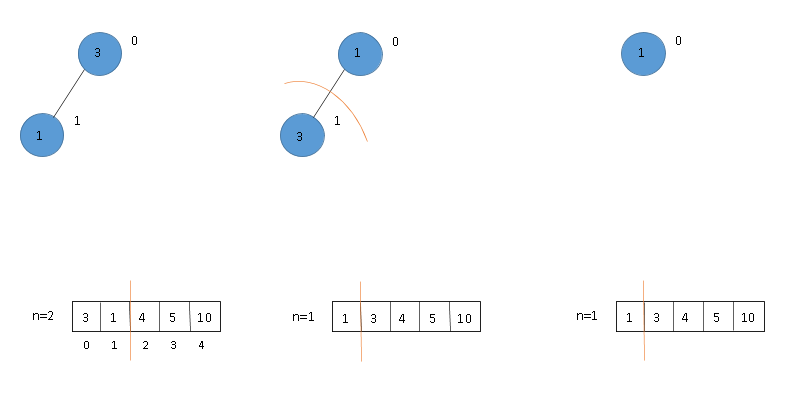
(2) Swap 1st and last node (3 and 1) and build heap. (3) Exclude last node and heapify. Final array is sorted.

Implementations

• C

#include <stdio.h>
void heapsort(int arr[], int n);
void heapify(int arr[], int n, int i);
void swap(int* a, int* b);
int main()
{
    int n, i;
    printf("Enter number of elements to input: ");
    scanf("%d", &n);
    int arr[n];
    printf("Enter the elements\n");
    for(i = 0; i < n; i++)
        scanf("%d", &arr[i]);
    heapsort(arr, n);
    printf("Elements after sorting\n");
    for(i = 0; i < n; i++)
        printf("%d ", arr[i]);
}
void heapsort(int arr[], int n)
{
    int i;
    // Build a max heap
    for(i = n/2 - 1; i >= 0; i--)
        heapify(arr, n, i);
    // One by one extract elements
    for(i = n-1; i >= 0; i--)
    {
        swap(&arr[0], &arr[i]);
        heapify(arr, i, 0);
    }
}
void heapify(int arr[], int n, int i)
{
    // initialize largest as root and get left and right nodes
    int largest = i;
    int left_node = 2*i + 1;
    int right_node = 2*i + 2;
    // Check if left node exists and is larger than root. If yes, change it
    if(left_node < n && arr[left_node] > arr[largest])
        largest = left_node;
    // Check if right node exists and is larger than root. If yes, change it
    if(right_node < n && arr[right_node] > arr[largest])
        largest = right_node;
    // change root, if needed
    if(largest != i)
    {
        swap(&arr[i], &arr[largest]);
        heapify(arr, n, largest);
    }
}
void swap(int* a, int* b)
{
    int temp = *a;
    *a = *b;
    *b = temp;
}

Applications

1. Finding extremas - Heap sort can easily be used find the maxima and minimum in a given sequence of numbers.
2. Job Scheduling - In Linux OS, heapsort is widely used for job scheduling of processes due to it's O(nlogn) time complexity and O(1) space complexity.
3. Graph Algorithms - It can used in the implementation of priority queue for Djikstra's algorithm, Prim's algorithm and Huffmann encoding as well.

Disadvantages

1. Heap sort is not a stable sort and requires constant space for sorting.
2. Memory management is quite complex due to heap data structure.

Questions