
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we will be discussing about the problem "BST to greater sum tree" in detail. This involve the concept of inorder traversal.
Contents:
- Introduction
- Optimized approach
- Implementation
- Code Explanation
- Time and Space Complexity Analysis
Introduction:
In this problem at OpenGenus, we are given a BST, and we have to transform key of every node of that BST into a greater sum tree where key of every node should be replaced by the sum of all keys greater than key of that node.
Note:
A binary search tree is a binary tree that satisfies below conditions:
- The left child's key of each node should be less than key of that node.
- The right child's key of each node should be greater than key of that node.
- Both the left and right subtrees should also be a binary search tree.
Example:
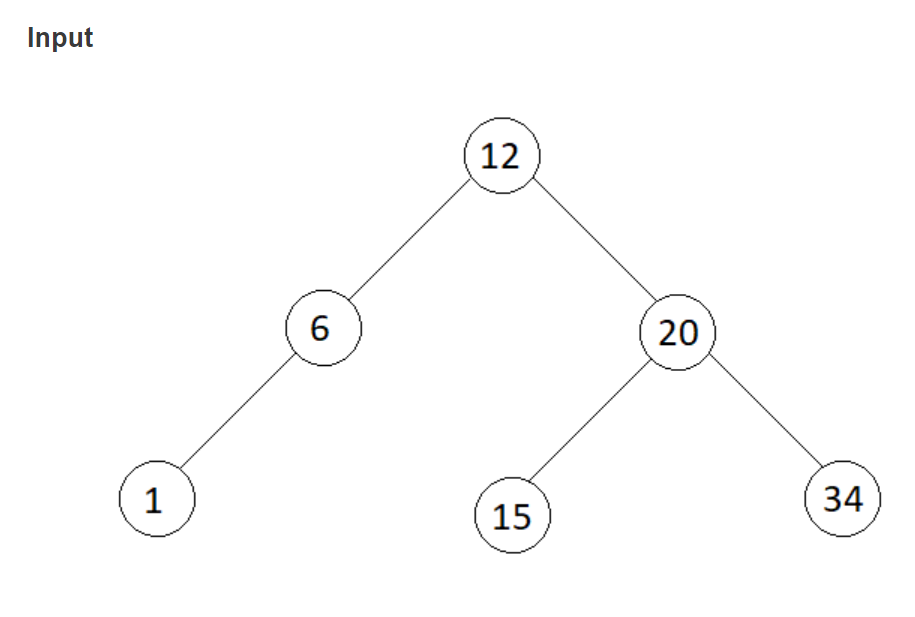
Here, in the above example we have to update the root node key with 20+15+34 = 69. Similarly its left child node key from 6 to 12+20+15+34 = 81 and its right child node key from 20 to 34 and so on.
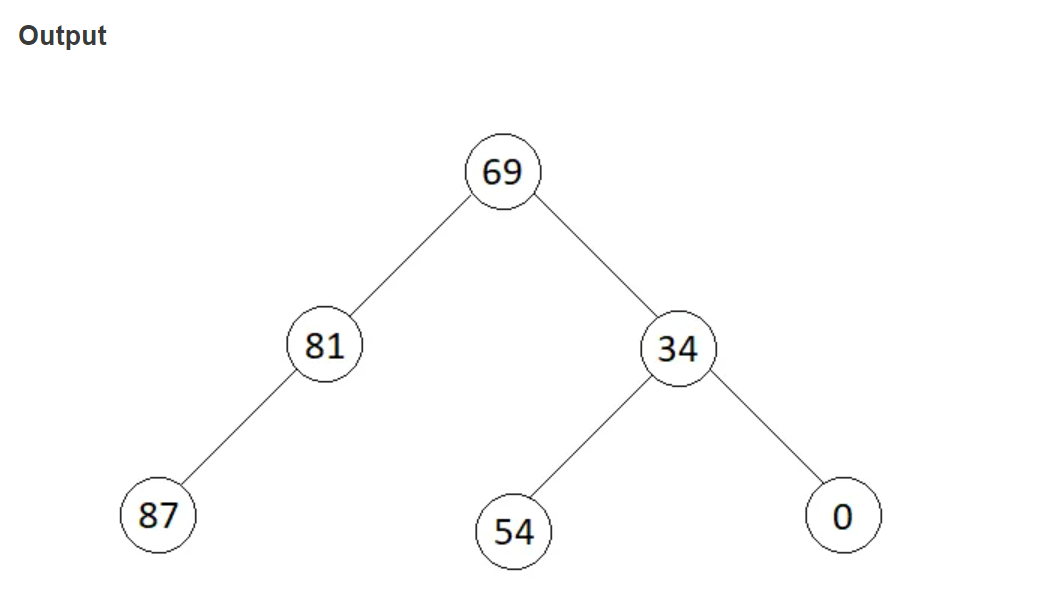
The above image shows the updated binary tree after replacing each node key by the sum of all keys greater than key of that node.
Optimized Approach:
In the optimized approach, first we will find the total sum of all the keys in the given binary search tree. Since the inorder traversal of a binary search tree is always sorted, therefore we will use this logic to update keys of each node with sum of all greater keys. We will recursively traverse the given BST in inorder manner and update key of each node with (total sum - sum of keys of previously traversed nodes).
Algorithm:
- Find total sum of the given binary tree recursively.
- Do a inorder traversal of the given binary tree and calculate currentSum for each node.
- The currentSum for a particular node is the total sum of keys less than key of that node.
- At last, update the key of each node by (total sum - currentSum of that node).
Implementation:
class Node{
int data;
Node left;
Node right;
Node(int data){
this.data = data;
left=null;
right=null;
}
}
class Solution
{
int currSum = 0;
public void transformTree (Node root)
{
//code here
int su = sum(root);
inOrder(root,su);
}
public int sum(Node root){
if(root==null){
return 0;
}
return(root.data+sum(root.left)+sum(root.right));
}
public void inOrder(Node root,int s){
if(root==null){
return;
}
inOrder(root.left,s);
currSum+=root.data;
root.data = s-currSum;
inOrder(root.right,s);
return;
}
}
public class Main{
static void printInorder(Node root)
{
if (root == null)
return;
printInorder(root.left);
System.out.print(root.data + " ");
printInorder(root.right);
}
public static void main(String args[])
{
Solution s = new Solution();
/* Constructed binary tree is
10
/ \
8 12
/
3
*/
Node root = new Node(10);
root.left = new Node(8);
root.right = new Node(12);
root.left.left = new Node(3);
System.out.println("Inorder Traversal of given tree");
printInorder(Root);
s.transformTree(root);
System.out.println("\n\nInorder Traversal of transformed tree");
printInorder(Root);
}
}
Code Explanation:
- We are creating a function transformTree() and passing the root node as a parameter in this function.
- This transformTree() function will first find the sum of all the keys in the given BST using the sum() function. This sum function will recursively traverse the given BST and add key of every node in the sum variable.
- After finding the total sum this transformTree() function will call the function inOrder() which will transform the given BST by traversing the tree in inorder manner.
Working of inOrder() function:
- This inOrder() function will traverse the given BST recursively in inorder manner.
- After the left sub-tree function call, we will update the currentSum by adding the keys of each node in ascending order (as we are traversing in Inorder manner).
- Then we will update key of each node with (total sum - currentSum).
- At last we will call the inOrder() function for the right subtree.
Time and Space Complexity Analysis:
The time complexity of the above solution will be O(N),where N is total number of nodes in the binary tree.
The space complexity of the above solution will be O(H), where H is the maximum height of the binary tree.
With this article at OpenGenus, you must have the complete idea of solving this problem "BST to greater sum tree".
