
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we have explored the concept of Almost complete binary tree.
Table of contents
- Tree
- Types of Trees
- Algorithm
- Conclusion
Tree
We are all familiar with tree from our childhood (like family tree). It has Roots, Branches and Leaves. In real life, this structure is used as leaves can be considered as children and branches can lead to its earliest known roots (i.e. parents to grandparents to great grandparents).
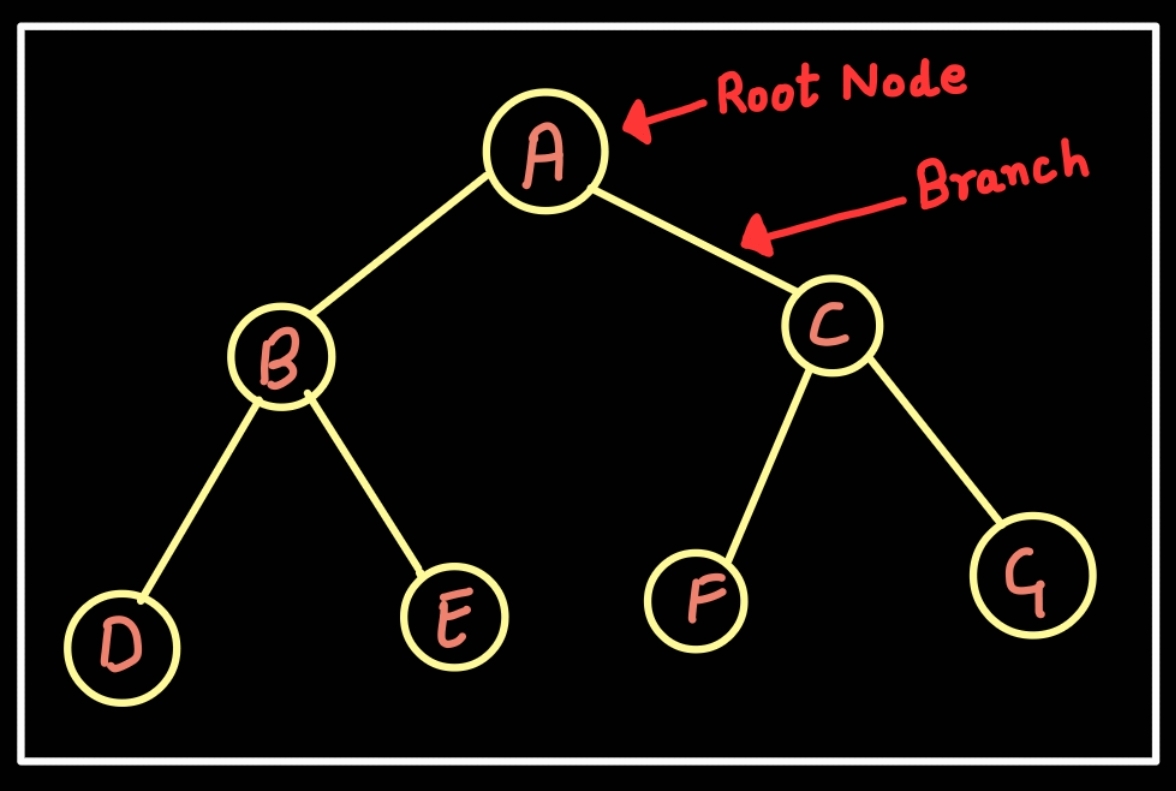
Here, A is parent of B and C, and grand-parent of D, E, F and G.
B is a parent of D and E, C is a parent of F and G.
D is called child of B. C is called child of A.
D and E are the siblings. Similarly, F and G are the siblings.
Tree data structure can be defined as a nonlinear and hierarchical data structure comprises a collection of nodes(such that node store the data/values). Each node in the tree data structure is connected to other nodes using branches/edges.
Types of Trees
- Binary Tree
- Binary search tree
- General Tree
- Balanced tree
Binary Tree
Binary Tree means that a node can have at most two childern, in simple terms a node can have either zero(0) or one(1) or two(2) children.
Binary Search Tree
Binary search tree means that the value of left node must be smaller than the parent node, and the value of right node must be greater than the parent node, and both subtrees of each node are also binary search trees. It is also called as sorted binary tree.
General Tree
General Tree means that a node can have either 0 or atmost n number of nodes. There is no restriction on the degree of the node.
Balanced Tree
Balanced tree means that a binary tree in which the height of the left and right subtree of every node differ by not more than 1.
Complete Binary Tree
Complete binary tree is a tree in which insertion takes place level by level and all the nodes are filled from left to right order/manner. It's last level might/might not be fully filled.
Almost Complete Binary Tree
Almost complete binary tree is a binary tree which satisfies following conditions:
- Insertion of nodes must takes place level by level and all the nodes must be left justified(i.e. from left to right).
- All the levels from 1 to n-1 level(n stands for number of levels) should be completely filled without any gap.
Important point is that if a node at level h (where h = 1 to n) has a right child, then it also has a left child.
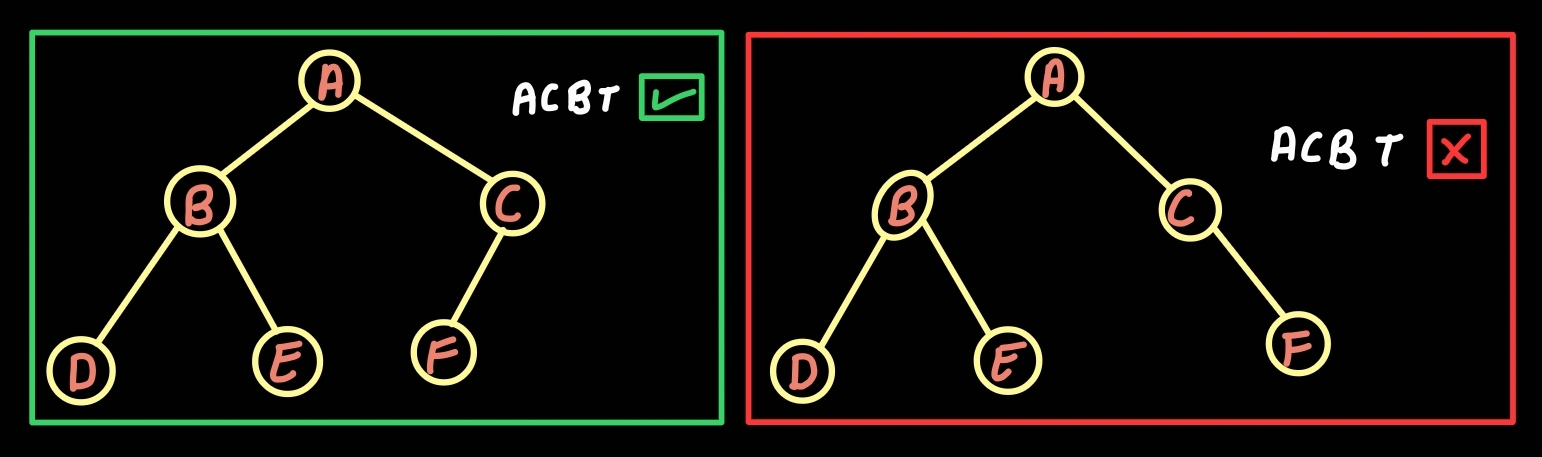
Here, ACBT stands for almost complete binary tree. In the above trees, left tree is a correct example of almost complete binary tree and right tree is an in-correct example of almost complete binary tree because at the last level, node left to node'F' is missing but according to the conditions of almost complete binary tree all nodes must be left justified.
- Almost complete binary tree is a complete binary tree till n-1 level.
- Almost complete binary tree is the subset of Complete binary tree(CBT), mean an almost complete binary tree will always be a complete binary tree.
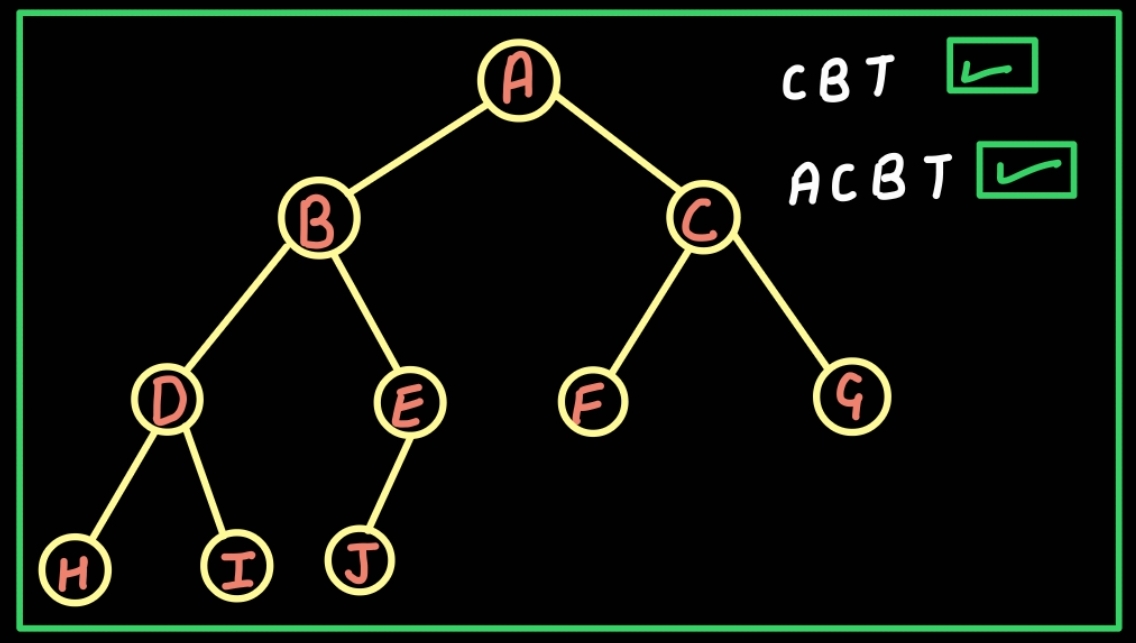
- Every formula that is applicable on complete binary tree is also applicable on almost complete binary tree.
- Almost complete binary tree can be used in Heap Data Structures.
Example
Let us take an example:
A
/ \
B C
/ \
D E
Here, above tree is a complete binary tree as well as almost complete binary tree both. Now, Lets do some operations on this tree, given below:
- Lets insert a new node 'F' in the tree.
A
/ \
B C
/ \ /
D E F
Here, according to the definition(above-mentioned), it is an almost complete binary tree as well as complete binary tree both.
2. Lets insert one more new node 'G' in the tree.
A
/ \
B C
/ \ / \
D E F G
Now, tree is a complete binary tree only, but according to the conditions of almost complete binary tree(above-mentioned) it is not an almost complete binary tree.
Again if we look closly at this tree, it is also a Full binary tree.
3. Now, Lets delete a node 'F' from the tree
A
/ \
B C
/ \ \
D E G
Now, After the deletion of node 'F', due to the violation of the rules it doesn't satisfy the definition. Therefore, this tree is neither an almost complete binary tree nor complete binary tree.
Check if tree is an almost complete binary tree or not?
procedure ACBT( root )
leaf <- 0
queue, enqueue the root node into queue
while( till queue is not empty )
{
temp, assign with dequeue front-node
condition-1: if( node have 0 child )
leaf <- 1
condition-2: if( a leaf-node has been already found and node is not a leaf-node )
return 0
condition-3: if(node have only right child)
return 0
condition-4: if( node have left child )
then enqueue node into queue
condition-5: if( node have right child )
then enqueue node into queue
}
return 1
end ACBT
- Begin ACBT
- We traverse through the nodes in level-order traversal.
- Take a flag variable let say leaf, values will be either 0 or 1, assign 0.
- Enqueue root into a queue to traverse through the node in level order and traverse until queue isn't empty.
- Condition-1: If current node is a leaf-node, then assign leaf as 1.
- Condition-2: If once a leaf-node has already been found and current node isn't a leaf-node, then return false.
- Condition-3: If only right child exist, then return false.
- Now, for condition 4 & 5, if left & right children exist respectively, then enqueue it.
- end ACBT
Implementation
#include <bits/stdc++.h>
using namespace std;
//--------Structure of Node-----------//
struct Node
{
char data;
Node * left, *right;
Node (char val)
{
data = val;
left = NULL;
right = NULL;
}
};
//-----Function to check if a given binary tree is an almost complete or not-----//
bool ACBT (Node * root)
{
if (root == NULL)
{
return 1;
}
list < Node * >q;
q.push_back (root);
bool leaf = 0;
while (!q.empty ())
{
Node * temp = q.front ();
q.pop_front ();
if (leaf == 0 && temp->left == NULL && temp->right == NULL)
{
leaf = 1;
}
if (leaf && (temp->left != NULL || temp->right != NULL))
{
return 0;
}
if (temp->left == NULL && temp->right)
{
return 0;
}
if (temp->left)
{
q.push_back (temp->left);
}
if (temp->right)
{
q.push_back (temp->right);
}
}
return 1;
}
//--------Driver function------------//
int main ()
{
/* Tree
A
/ \
B C
/ \ /
D E F
*/
Node * root = new Node ('A');
root->left = new Node ('B');
root->right = new Node ('C');
root->left->left = new Node ('D');
root->left->right = new Node ('E');
root->right->left = new Node ('F');
if (ACBT (root))
{
cout << "Almost complete binary tree" << endl;
}
else
{
cout << "Not an almost complete binary tree" << endl;
}
return 0;
}
Complexity
Time Complexity: O(N), due to loop.
Space Complexity: O(N), because it traverse through every node.
Conclusion
Most of people are confused in the difference between Complete binary tree and Almost complete binary tree. Therefore, The only difference is that a complete binary tree might/ might not be fully filled but an Almost complete binary tree might not be fully filled.
