
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we will be discussing about the problem "Extreme nodes in alternate order in a Binary tree" in detail. This involve the concept of Breadth First Search (BFS) and Level order traversal.
Contents:
- Introduction
- Optimized approach
- Implementation
- Code Explanation
- Time and Space Complexity Analysis
Introduction:
In this problem at OpenGenus, we are going to print the extreme nodes at each level but in the alternate order in a binary tree i.e, in the first level we'll print the left-most node but in the second level we'll print the right-most node. Similarly in third level we'll print the left-most node and so on. we will print the extreme nodes of each level till the last level of the binary tree.
Example 1:
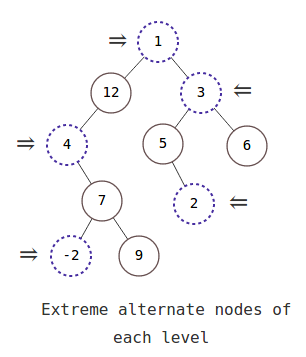
In the above example we can see the extreme nodes at each level. so in the above example our output will be [1,3,4,2,-2]
Example 2:

Similarly in the example 2, the extreme nodes at each level will be: 5,8,11,5. so, the output will be [5,8,11,5]
Optimized Approach:
In the optimized approach, we will traverse the given binary tree in a breadth first search manner or level order traversal using queue data structure. For each level of traversal we will print the left extreme node or right extreme node of that level depending on the level of the binary tree. If the level of binary tree is odd then we will print the left extreme node and if the level of the binary tree is even then we will print the right extreme node of that level. we will consider the root node as the first level and it child nodes as second level and so on.
Algorithm:
- Traverse the given binary tree in a level order manner.
- Create a variable x which will store the current level that we are traversing.
- If the value of x is odd add first element of that level in the list.
- If the value of x is even add last element of that level in the list.
Implementation:
import java.util.*;
class Node{
int data;
Node left;
Node right;
Node nextRight;
Node(int data){
this.data = data;
left=null;
right=null;
nextRight = null;
}
}
class Solution{
public static ArrayList<Integer> extremeNode(Node root)
{
//add code here.
ArrayList<Integer> list = new ArrayList<Integer>();
Queue<Node> q = new LinkedList<Node>();
q.add(root);
int x = 0;
while(q.isEmpty()==false){
int count = q.size();
for(int i = 0; i<count;i++){
Node curr = q.poll();
if(x%2!=0 && i==count-1){
list.add(curr.data);
}
if(x%2==0 && i==0 ){
list.add(curr.data);
}
if(curr.left!=null){
q.add(curr.left);
}
if(curr.right!=null){
q.add(curr.right);
}
}
x++;
}
return list;
}
public static void main(String args[])
{
/* Constructed binary tree is
10
/ \
8 2
/
3
*/
Node root = new Node(10);
root.left = new Node(8);
root.right = new Node(2);
root.left.left = new Node(3);
System.out.println(extremeNode(root));
}
}
Code Explanation:
- We are creating a function extremeNode() and pass the root node as a parameter in this.
- This function will return an ArrayList containing all the extreme nodes but in the alternate order by using level order traversal.
- If you don't know how level order traversal of a binary tree works using a queue data structure, first you can go through this https://iq.opengenus.org/level-order-traversal-binary-tree/.
- In level order traversal, if we are traversing the last node of a particular level then all the node of its next level must have been added to the queue till then and all the nodes of that level must been removed from the queue.
- So we will be creating a variable count to get the total count of nodes at a particular level and a variable x to get the information about the current level and will be incrementing x after we reach the last node of a particular level.
- If the value of x is odd then we will add the value of left extreme node to our list but if the value of x is even then we will add the value of right extreme node to our list.
- If the queue becomes empty, then we have traversed the whole binary tree. Therefore, we will return the list.
Time and Space Complexity Analysis:
The time complexity of the above solution will be O(N),where N is total number of nodes in the binary tree. As in the above approach we are doing complete traversal of the binary tree, so the overall complexity of the above solution will be O(N).
The space complexity of the above solution will be O(N), where N is total number of nodes in the binary tree. Since we are creating a queue data structure and at a time the maximum nodes that the queue will store is the all nodes of a particular level which will be maximum width of the binary tree. The maximum width of binary tree can be N/2 if it is complete binary tree, so the overall space complexity of the above solution will be O(N).
With this article at OpenGenus, you must have the complete idea of solving this problem "Extreme nodes in alternate order in a Binary Tree".
