Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Given a binary tree, we are supposed to traverse the tree using the level order traversal. Level order traversal is just another word for the Breadth First Traversal i.e. traverse the tree level-by-level. Contrary to Depth First Traversal, where we traverse deeper into the tree, level order traversal (or breadth first traversal or breadth first search) traverses every node in a level before going into the next level. The search tree is broadened on each level before going into another level.
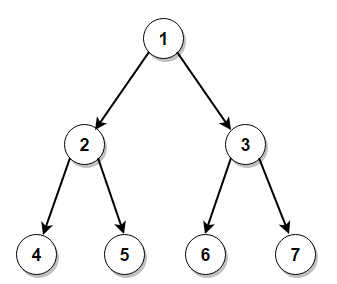
Let us understand this using a figure.
The following tree shows a simple binary tree with its root at 1 and following children nodes. The level order traversal would be 1, 2, 3, 4, 5, 6, 7 as the search tree would be start at the root and progressively go down each level and traverse the nodes in a level order.
Idea behind solving this problem
1. Using a function to print a given level
This approach uses the help of two functions: one function prints all nodes at a given level (we will call that function printGivenLevel). The other function prints the level order traversal of the binary tree (we will call that function printLevelOrderTraversal). printLevelOrderTraversal uses the printGivenLevel as a helper function to print nodes at all the levels one by one. The function starts from the root. The algorithm for this approach is given below.
/*Function that prints level order traversal of binary tree*/
printLevelorderTraversal(tree)
for d = 1 to height(tree)
printGivenLevel(tree, d);
/*Function that prints all nodes at a given level*/
printGivenLevel(tree, level)
if tree is NULL then return;
if level is 1, then
print(tree->data);
else if level greater than 1, then
printGivenLevel(tree->left, level-1);
printGivenLevel(tree->right, level-1);
2. Using a queue
In this approach, first the node is visited and then it’s subsequent child nodes are put in a FIFO queue. This is done for all the nodes in the binary tree. This approach uses extra space in the form of the FIFO queue but is optimal than the first approach where we use the function to traverse the binary tree. The space-time complexity is discussed after the code implementation. The algorithm for this approach is shown below.
printLevelOrderTraversal(tree)
Create an empty queue q
temp_node = root /*start from root*/
Loop while temp_node is not NULL
print temp_node->data.
Enqueue temp_node’s children (first left then right children) to q
Dequeue a node from q.
Code Implementation
Below is the code implementation of both the solutions: using the function as well as using queue. The language of preference is C++. I have also created a Github repository that has the presented solution here as well as a solution in Python. You can visit this link if you wish to see the repository.
1. Using function to print the level order traversal
#include <iostream>
using namespace std;
// Data structure to store a binary tree node
struct Node
{
int key;
Node *left, *right;
Node(int key)
{
this->key = key;
this->left = this->right = nullptr;
}
};
// Function to print all nodes of a given level from left to right
bool printGivenLevel(Node* root, int level)
{
if (root == nullptr) {
return false;
}
if (level == 1)
{
cout << root->key << " ";
// return true if at least one node is present at a given level
return true;
}
bool left = printGivenLevel(root->left, level - 1);
bool right = printGivenLevel(root->right, level - 1);
return left || right;
}
// Function to print level order traversal of a given binary tree
void printLevelOrderTraversal(Node* root)
{
// start from level 1 — till the height of the tree
int level = 1;
// run till `printGivenLevel()` returns false
while (printGivenLevel(root, level)) {
level++;
}
}
int main()
{
Node* root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->left->right = new Node(5);
root->right->left = new Node(6);
root->right->right = new Node(7);
printLevelOrderTraversal(root);
return 0;
}
2. Using queue for level order traversal
#include <iostream>
#include <list>
using namespace std;
// Data structure to store a binary tree node
struct Node
{
int key;
Node *left, *right;
Node(int key)
{
this->key = key;
this->left = this->right = nullptr;
}
};
// Function to print level order traversal of a given binary tree
void printLevelOrderTraversal(Node* root)
{
// create an empty queue and enqueue the root node
list<Node*> queue;
queue.push_back(root);
// pointer to store the current node
Node* curr = nullptr;
// loop till queue is empty
while (queue.size())
{
// process each node in the queue and enqueue their
// non-empty left and right child
curr = queue.front();
queue.pop_front();
cout << curr->key << " ";
if (curr->left) {
queue.push_back(curr->left);
}
if (curr->right) {
queue.push_back(curr->right);
}
}
}
int main()
{
Node* root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->left->right = new Node(5);
root->right->left = new Node(6);
root->right->right = new Node(7);
printLevelOrderTraversal(root);
return 0;
}
Space and Time complexity analysis
1. Using function
Time Complexity: O(n^2) in worst case. Why? Well, for a skewed tree, printGivenLevel() takes O(n) time where n is the number of nodes in the skewed tree. So time complexity of printLevelOrderTraversal() is O(n) + O(n-1) + O(n-2) + ... + O(1) which is O(n^2).
Space Complexity: O(n) in worst case since for a skewed tree, printGivenLevel() uses O(n) space for call stack. For a Balanced binary tree, the call stack uses O(log n) space, which is the height of the balanced tree.
2. Using queue
Time Complexity: O(n) where n is number of nodes in the binary tree
Space Complexity: O(n) where n is number of nodes in the binary tree (we use to store the child nodes for the specific node)
We see that the queue method is optimal than using functions to traverse a binary tree level by level. However, the queue method uses extra space to store the child nodes of a specific node.