Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Degenerate or Pathological Tree is a variant of Binary Tree which we have explored in depth along with code implementation for Degenerate or Pathological Tree.
Before we look into a degenerate tree, you need to have knowledge on Binary Search Tree. So we'll look into the binary search tree first.
Binary Search Tree
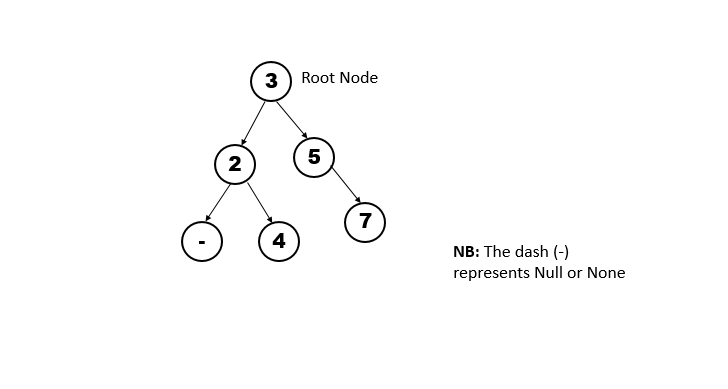
This is a type of tree data structure in which the leaf nodes (child nodes) are stored in relation to the value of the parent node, if the value of the node to be inserted is less than that of its parent node, then it is set as the left child of the parent node, else, it is set as the right child of the parent node. That is, assuming we want to store the following values in a BST: 3, 2, 5, 4, 7.
This is how it will look like
How to implement a Binary Search Tree?
I'll write out the code and explain afterwards
#python3
class Node:
def __init__(self, value):
self.value = value
self.rightNode = None
self.leftNode = None
class BinarySearchTree:
def __init__(self):
self.root = None
# This method represents the graph as an adjacency list
def getTreeMap(self):
treeMap = {}
if self.root is None:
return treeMap
queue = [self.root]
while len(queue) > 0:
currentNode = queue.pop(0)
# currentNode is our key now
treeMap[currentNode.value] = []
if currentNode.leftNode:
treeMap[currentNode.value].append(currentNode.leftNode.value)
queue.append(currentNode.leftNode)
if not currentNode.leftNode:
treeMap[currentNode.value].append(None)
if currentNode.rightNode:
treeMap[currentNode.value].append(currentNode.rightNode.value)
queue.append(currentNode.rightNode)
if not currentNode.rightNode:
treeMap[currentNode.value].append(None)
return treeMap
def insert(self, value):
node = Node(value)
if self.root is None:
self.root = node
queue = [self.root]
while len(queue) > 0:
currentNode = queue.pop(0)
if node.value < currentNode.value:
if currentNode.leftNode:
queue.append(currentNode.leftNode)
else:
currentNode.leftNode = node
elif node.value > currentNode.value:
if currentNode.rightNode:
queue.append(currentNode.rightNode)
else:
currentNode.rightNode = node
return True
We start off by implementing a Node class, since a BST is a Tree data structure that consists of nodes and edges.
The Node class consists of a value, a right child and a left child, in which both are set to None.
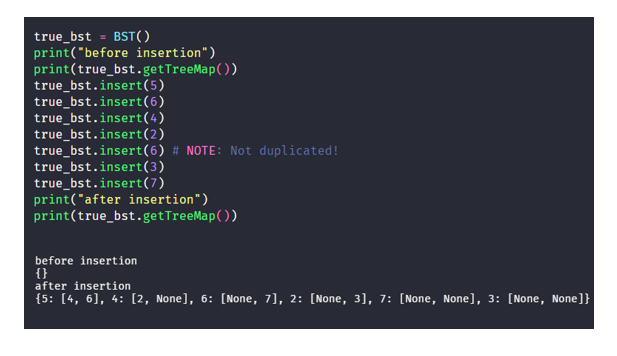
In the main BinarySearchTree class, I only implement 2 methods, getTree() which prints out the tree structure and insert() method which allows us to insert a node to the tree.
Our main focus though, is the insert() method.
As with any tree data structure, we need a root node, in this case, the root node is set to None when the BST is initialized, this illustrates that the Tree is empty.
The insert method takes in a parameter which is a value. From this value, a node is constructed using the Node class.
We then check whether the tree has a root Node, if not, we set the new node as the root node
If the tree does have a root node, then we need to traverse the nodes until we find the right place to place the new node. The right place for the new node depends on the fact that:
- If the value of the node is less than that of the parent node, it is set as the left child.
- If the vaue of the node is greater than that of the parent node, it is set as the right child.
- Should NOT store a duplicate value
The above criteria is checked by the code below that belongs to the insert method.
if node.value < currentNode.value: # handles criteria 1
if currentNode.leftNode:
queue.append(currentNode.leftNode)
else:
currentNode.leftNode = node
elif node.value > currentNode.value: # handles criteria 2
if currentNode.rightNode:
queue.append(currentNode.rightNode)
else:
currentNode.rightNode = node
Lets test this out.
Introduction to Degenerate Trees
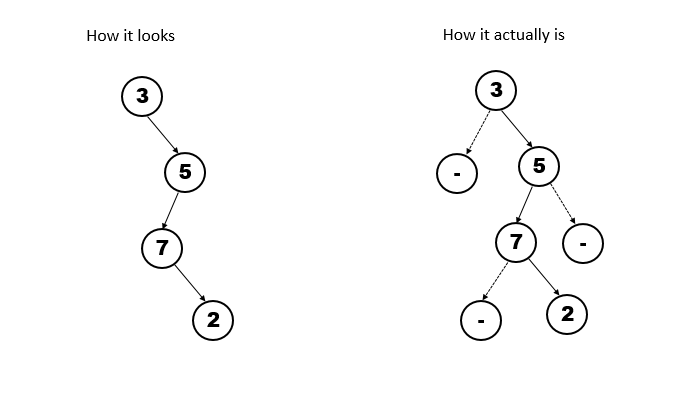
Now that we know about BST, it will be easier to understand Degenerate Trees. A Degenerate Tree is also called a Pathological Tree. It is a type of BST in which each node has only one child node. So it bascially looks something like this.
A degenerate tree can take different forms. The above image is just one way it could be and how we are going to implement it, The main criteria to recognize a degenerate tree is that each parent node has only one associated child node.
Which brings me to my next case, That sounds like a linked list, so what is the difference between a degenerate tree and a linked list? I'll point out one, A linked list points to only one node, even though a degenerate tree has only one child node, this is only because the other child node is Null.
Next we look at how to implement a degenerate tree to get a similar structure as the one in the image.
How to implement a Degenerate Tree
I'll write the code then discuss it.
class DegenerateTree:
def __init__(self):
self.root = None
def getTreeMap(self):
treeMap = {}
if self.root is None:
return treeMap
queue = [self.root]
while len(queue) > 0:
currentNode = queue.pop(0)
# currentNode is our key now
treeMap[currentNode.value] = []
if currentNode.leftNode:
treeMap[currentNode.value].append(currentNode.leftNode.value)
queue.append(currentNode.leftNode)
if not currentNode.leftNode:
treeMap[currentNode.value].append(None)
if currentNode.rightNode:
treeMap[currentNode.value].append(currentNode.rightNode.value)
queue.append(currentNode.rightNode)
if not currentNode.rightNode:
treeMap[currentNode.value].append(None)
return treeMap
def insert(self, value):
node = Node(value)
if self.root is None:
self.root = node
return True
queue = [self.root]
toRight = True
while len(queue) > 0:
currentNode = queue.pop(0)
if toRight:
toRight = False
# print("need to put it on the right")
if currentNode.rightNode is None:
# There is no right node
currentNode.rightNode = node
return True # inserted successfully
else:
queue.append(currentNode.rightNode)
else:
# print("need to put it on the left")
toRight = True
if currentNode.leftNode is None:
currentNode.leftNode = node
return True
else:
queue.append(currentNode.leftNode)
def search(self, value):
if self.root is None:
return False # Tree is empty
queue = [self.root]
while len(queue) > 0:
currentNode = queue.pop()
if currentNode.value == value:
return True
elif currentNode.rightNode:
queue.append(currentNode.rightNode) # 0(1)
elif currentNode.leftNode:
queue.append(currentNode.leftNode)
return False # Not in the Tree
def delete(self, value):
if self.root is None:
return False
if self.root.value == value:
# delete root and make its child the new root
if self.root.rightNode:
self.root = self.root.rightNode
return True
elif self.root.leftNode:
self.root = self.root.leftNode
return True
return True
queue = [self.root]
while len(queue) > 0:
currentNode = queue.pop(0)
rightChild = currentNode.rightNode
leftChild = currentNode.leftNode
if rightChild and rightChild.value == value:
# print("found the value: ", rightChild.value)
currentNode.rightNode = rightChild.rightNode
currentNode.leftNode = rightChild.leftNode
return True
elif leftChild and leftChild.value == value:
# print("found the value: ", leftChild.value)
currentNode.rightNode = leftChild.rightNode
currentNode.leftNode = leftChild.leftNode
return True
if rightChild:
queue.append(rightChild)
elif leftChild:
queue.append(leftChild)
return False
The code looks overwhelming, but, I'll go through every method. Since we are analyzing the time complexity of a degenerate tree, we will be looking at 3 operations: Insert, Search and Delete.
Analyzing the Insert Operation
def insert(self, value):
node = Node(value)
if self.root is None:
self.root = node
return True
queue = [self.root]
toRight = True
while len(queue) > 0:
currentNode = queue.pop(0)
if toRight:
toRight = False
# print("need to put it on the right")
if currentNode.rightNode is None:
# There is no right node
currentNode.rightNode = node
return True # inserted successfully
else:
queue.append(currentNode.rightNode)
else:
# print("need to put it on the left")
toRight = True
if currentNode.leftNode is None:
currentNode.leftNode = node
return True
else:
queue.append(currentNode.leftNode)
From the value given, we first have to create a new node. The value could simply be an integer, but the node is an object that has the right child and left child attributes.
After creating a new node, we check if the tree is empty, which means it does not have a root node. If it is empty, we set the new node as the root and return.
If the root is not empty, it means we have nodes in our tree and thus we have to traverse through the tree until we get to the end and insert our new node at the end. For the insert method, we insert a new node at the end of the tree. Thus, the Time complexity for this operation is O(h) where h is the height of the tree or simply the number of nodes in the tree. Notice that it has the same time complexity as that of inserting an node in a linked list.
Lets take a more closer look at why this is true.
In our algorithm, assuming the tree has some nodes.
Notice that we have a toRight variable that holds a boolean value, this only tells us in which side should the child node be set to, whether its a right child node or left child node. Again, NOTE that this is ONLY due to the structure of my degnerate tree.
- We create a queue which at the start only contains the root node, because we need a starting point for our traversal.
- As long as the queue is not empty, meaning we are not at the end of the tree, we keep on traversing.
- In every step of a traversal,
- We first check the value of the
toRightvariable, if it is True, means that we should set the new node as the right child, that is, if it does not exist. - If the current node contains a right child, then we get that child and place it in the queue and set the
toRightvariable toFalse - If the
toRightvariable is set to False, means that we should set the new node as the left child, that is, if it does not exist. - If the child node does exist, meaning we need to keep on traversing the tree, thus we add this node to the queue, for its traversal too.
Analyzing the Search Operation
Lets take a look at how the search operation works.
def search(self, value):
if self.root is None:
return False # Tree is empty
queue = [self.root]
while len(queue) > 0:
currentNode = queue.pop()
if currentNode.value == value:
return True
elif currentNode.rightNode:
queue.append(currentNode.rightNode)
elif currentNode.leftNode:
queue.append(currentNode.leftNode)
return False # Not in the Tree
Taking the worst case senario, the time complexity of a search operation is also O(h) where h is the height of the tree or the total number of nodes. Here's why:
We have to traverse through the whole tree (in worst case) to find the node we are looking for.
Assuming we have nodes in our tree,
1.We first create a queue which holds the root node as a starting point for traversal.
2.while there are still elements in the queue
3.We get the first item from the queue and set it as the current node,
4.We then check its value against the one we are searching for,
5.If it is the value, we return True,
6.If it is not the value, we add the node to the queue. NOTE: Remember that every node has 2 children, but one is set as None, thus it officially only has 1 child. In the search() method, we have checks, if statments that add the child to the queue only if it is True.
7.At the end of the loop, if the value is not found, then it is not in the tree, thus, False is returned.
Analyzing the Delete Operation
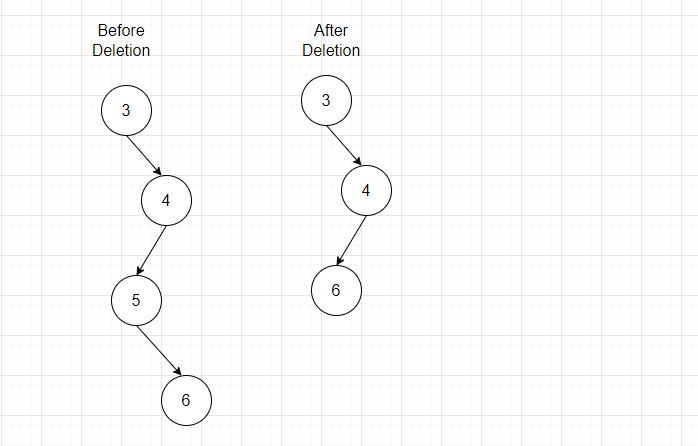
The delete operation for a degenerate tree is also not different from that of a linked list, since we only expect one child node. All we have to do is remove the node with the value we want to delete, and afterwards, take its child and make it the child of the parent node of the node being deleted.
Like this:
Notice that we don't need to change anything else apart from the pointer of the parent node to point to its "grandchild" instead of the child node since we will be deleting the child node.
def delete(self, value):
if self.root is None:
return False
if self.root.value == value:
# delete root and make its child the new root
if self.root.rightNode:
self.root = self.root.rightNode
return True
elif self.root.leftNode:
self.root = self.root.leftNode
return True
return True
queue = [self.root]
while len(queue) > 0:
currentNode = queue.pop(0)
rightChild = currentNode.rightNode
leftChild = currentNode.leftNode
if rightChild and rightChild.value == value:
# print("found the value: ", rightChild.value)
currentNode.rightNode = rightChild.rightNode
currentNode.leftNode = rightChild.leftNode
return True
elif leftChild and leftChild.value == value:
# print("found the value: ", leftChild.value)
currentNode.rightNode = leftChild.rightNode
currentNode.leftNode = leftChild.leftNode
return True
if rightChild:
queue.append(rightChild)
elif leftChild:
queue.append(leftChild)
return False
The time complexity for a delete operation on a degenerate tree is also O(h) where h is the height of the tree or number of nodes. Here's why. We need to traverse through the whole tree (taking the worst case senario) in order to find the node for deletion. NOTE: You should note that in case the node we are deleting is the root node, then the time complexity for a deletion operation is O(1) (constant time). Although, this is the best case senario.
Befor I explain the code, This is an overview of how it works.
There are 3 cases that can occurr.
- The node we want to delete is the root node (first node in the tree).
- The node we want to delete is in the middle (has a parent and has a child).
- The node we want to delete is the last node (has a parent but no child).
For the first case, we can simply handle it by checking the value of the root node and if its the case, then we set either its right child or left child as the new root node, depending on which one is not Null.
For the second case, we need to traverse through the whole tree (since we are unaware of where the node actually is). We have a queue to keep track of the queue to traverse. Starting from the root node.
In every step of the traversal, we take the first element from the queue and set it as our current node denoting where we are in our traversal. We then check if the current node has a right child and that it is the node we want to delete from the tree. This next part is confusing, so instead, I am going to use an illustration to explain. Assuming we are at node A (our current node) and node A has a right child node B which in turn has either a right or left child node C.
If we want to delete node B, we first has to set the right child of node A as node C, thus node B has been unlinked from node A. The same happens if the current node has a left child and not a right child.
And thats exactly what we do in the code, afterwards, we just return True if the node was deleted, else, we keep on traversing the tree by adding the child node of the current node to the queue.
After the while loop is completed, meaning that we have reached the end of the tree and not found the node, we simply return False.
NOTE: Handling the second case, handles the 3rd case by default. Since the 3 case states that we need to delete a node that is at the end of the tree. So it has no child.
Here is my takeaway for you. Remember how talked about unlinking the node we want to delete. Where does it go?
Thanks for reading the article at OpenGenus and hope it helps.