
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we have explained the algorithm to find the Bottom view of a Binary Tree.
Table of contents
- What is Binary Tree?
- What is Bottom view of a binary tree?
- Algorithm
- Code
- Complexity
What is Binary Tree?
Here, Binary itself mean two.
Binary Tree means that a node can have at most two childern, in simple terms a node can have either zero(0) or one(1) or two(2) children.
Some properties of Binary Tree:
- Each i-th level of binary tree, the maximum number of nodes are 2^i.
- If Binary tree has height 'h', then
- Minimium number of nodes are h+1 (i.e. when we have right skewed binary tree or left skewed binary tree)
- Maximum number of nodes are 2^(h+1)-1 (i.e. when we have a completely full binary tree)
Question
What is the maximum height 'h' of a tree, if 'n' number of nodes are given?
What is Bottom view of Binary tree?
The bottom view of a binary tree refers to the bottom-most nodes of tree present at their horizontal distance, We print the bottom view nodes from left to right.
We consider the horizontal distance for bottom view of binary tree is defined as follows:
- Horizontal distance of root from itself is zero (0).
- Horizontal distance of right child of root node is one (1).
- Horizontal distance of left child of root node is minus one (-1).
For the nodes of a bottom view of binary tree, horizontal distance is as follows:
- Horizontal distance of left child of a node is equal to horizontal distance of its parent minus-one.
- Horizontal distance of right child of a node is equal to horizontal distance of its parent plus one.
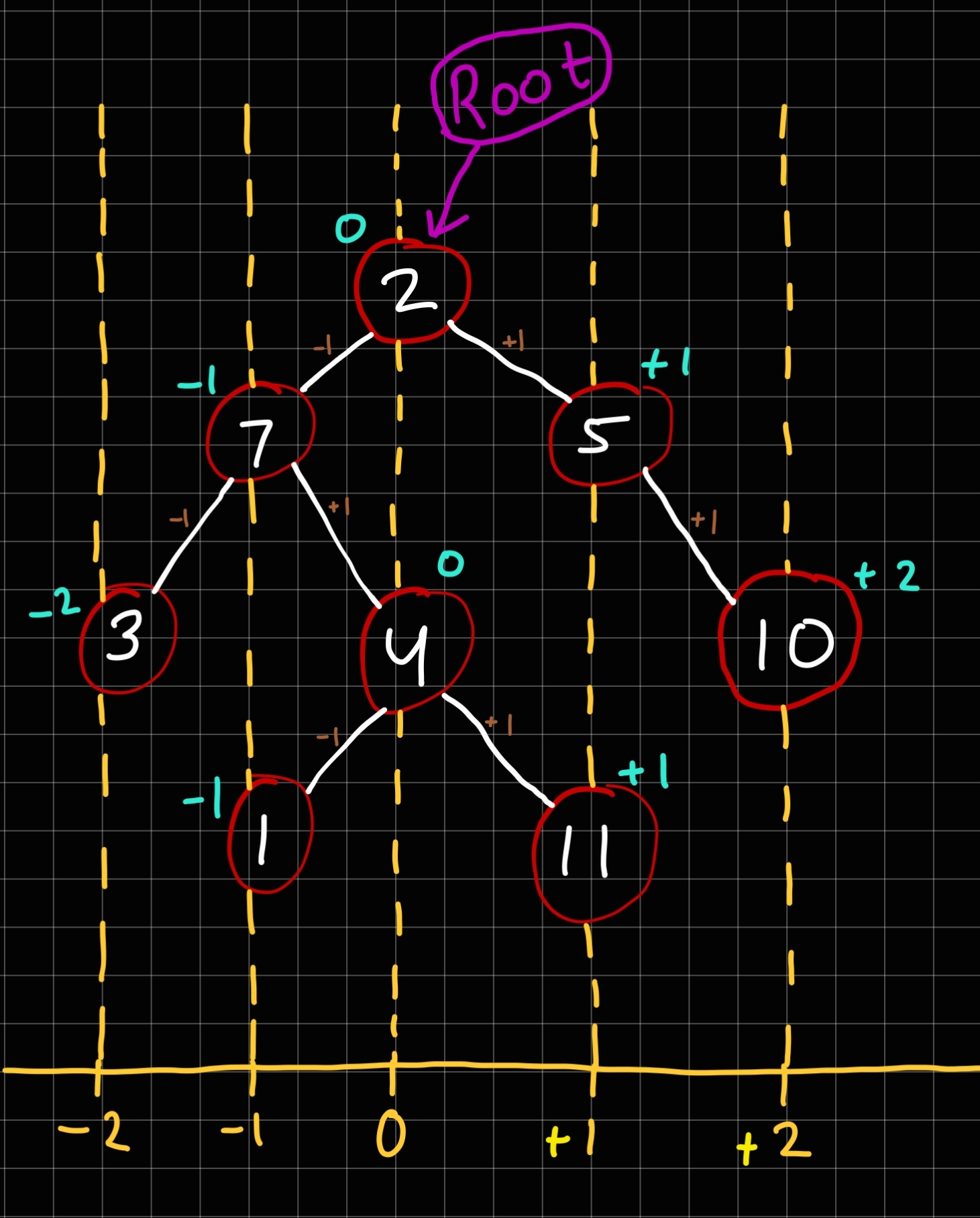
Here in this picture, we can all the points as above mentioned.
- Horizontal distance of 3 is minus-two(-2).
- Horizontal distance of 1 is minus-one(-1).
- Horizontal distance of 4 is zero(0).
- Horizontal distance of 11 is one(+1).
- Horizontal distance of 10 is two(+2).
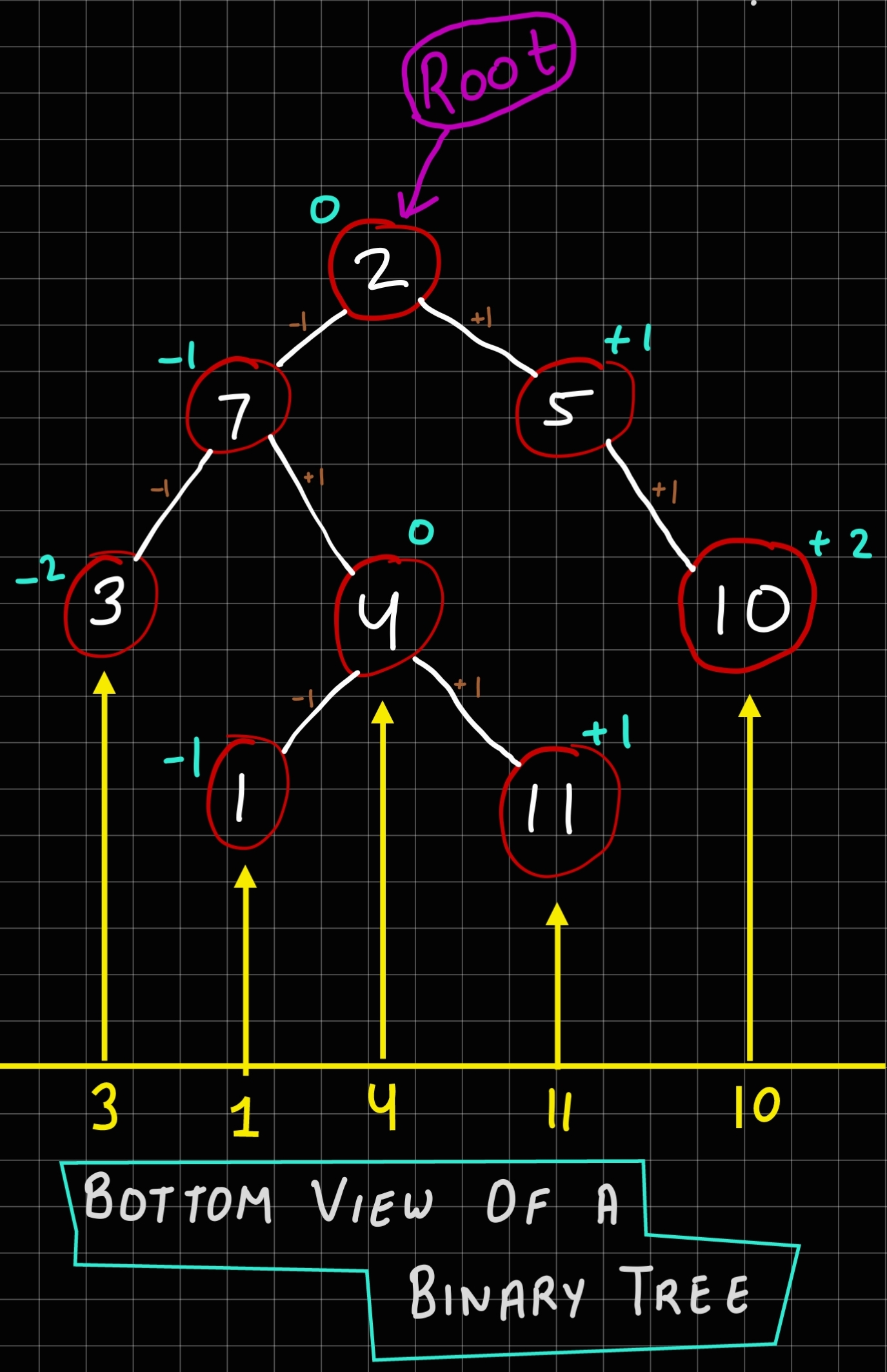
Bottom view nodes in the tree are 3, 1, 4, 11, 10 moving from left to right direction.
Algorithm for Bottom view of Binary tree
- Create/Initialize a map having horizontal distance and a pair (x , y), where :
- x is the value of the Node.
- y is the height/level of the Node.
map looks like (horizontal distance → ( x , y ))
- Now, we will perform the pre-order traversal to calculate the horizontal distance of each node.
- If Current-Node is NULL, do nothing and return.
- If current-Node is not NULL,then:
- Insert/Add the current node to the result/map, if the current-node at a horizontal distance is first we have seen.
- Else, If a node exists in the map for a particular horizontal distance, then only replace/update that node with the current-node if the current-node is at a height/level greater than that of the already added node.
- After completion of above steps, our map is completely updated with keys(horizontal distance). All we need to do is print out the values in this map to get the bottom-View.
(-2 → ( 3 , 3 ))
(-1 → ( 1 , 4 ))
(0 → ( 4 , 3 ))
(1 → ( 11 , 4 ))
(2 → ( 10 , 3 ))
Code
//Structure for Bottom view of Binary Tree
struct B_Node
{
int value; //value of the node
int h; // horizontal distance of the node
B_Node * left, * right; //left and right
B_Node(int key) //Constructor of tree node
{
value=key;
h=INT_MAX;
left=right=NULL;
}
};
void Bottom_view(B_Node * root, int c, int h, map<int, pair<int, int>> & a)
{
if(root==NULL) //if have zero or no node
return;
if (a.find(h)==a.end()) //checking if horizontal distance is in the map or not, if not in the map then insert it.
{
a[h] = make_pair(root->value, c);
}
//if horizontal distance is present in the map then compare the levels with the present node, if greater than that of already present node, then replace it.
else
{
pair<int, int> p=a[h];
if (p.second<=c)
{
a[h].second=c;
a[h].first=root->value;
}
}
Bottom_view(root->left, c+1, h-1, a);
Bottom_view(root->right, c+1, h+1, a);
}
void Bottomview(B_Node * root)
{
map<int, pair<int, int>> a; //creating a map to store the value of horizontal distance as key and a pair of height/levels and value of the node.
Bottom_view(root, 0, 0, a); //calling the Bottom_view() to get the values
map<int, pair<int, int>> ::iterator i; //Printing the value stored by Bottom_view() using iteration
for (i=a.begin(); i!=a.end(); ++i)
{
pair<int, int> p=i->second;
cout<<p.first<<" ";
}
}
Complexity/Order of the Algorithm
Time Complexity is O(n).
Space Complexity is O(n).
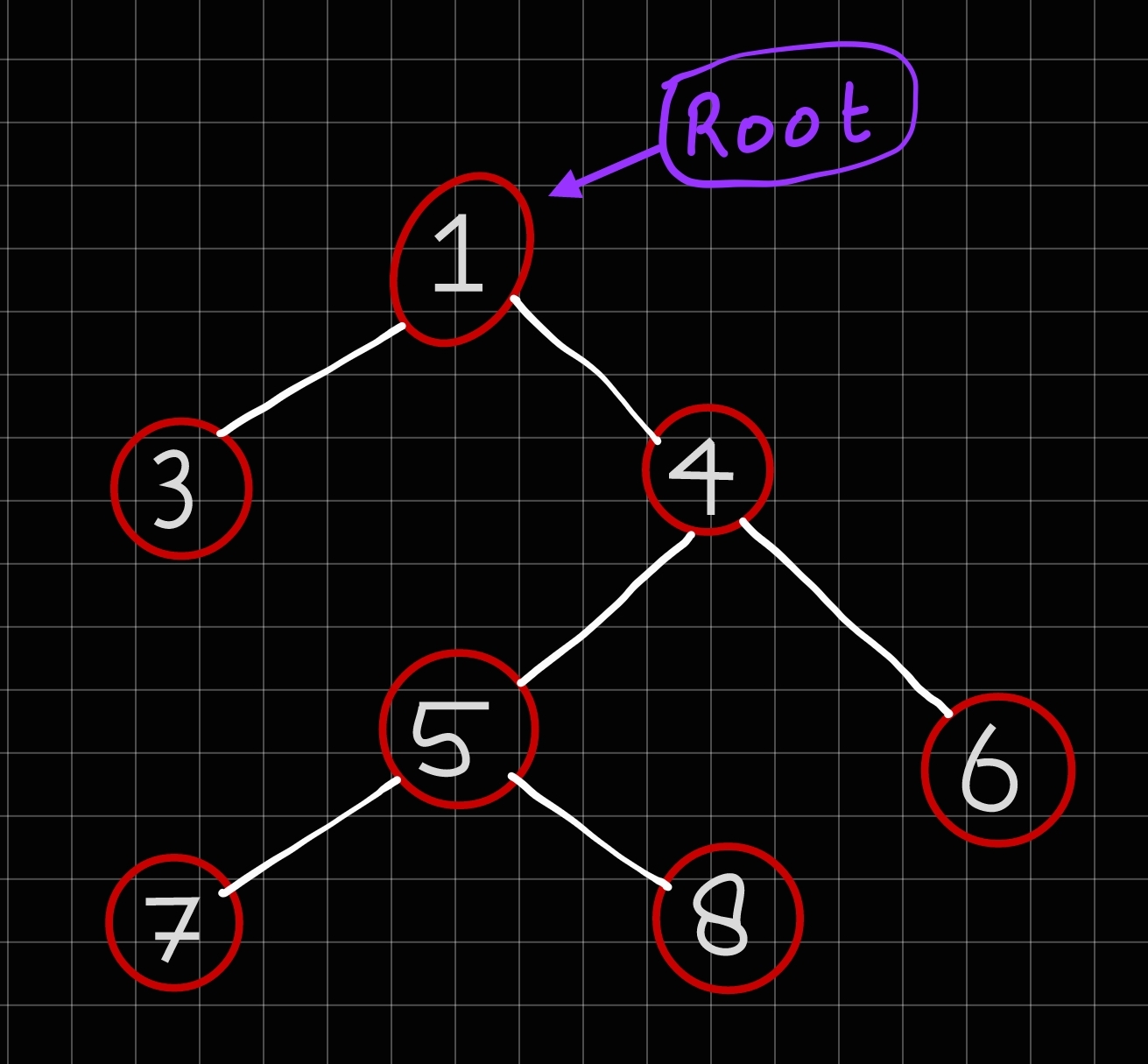
Question
What are the Bottom view Nodes in the below given Binary Tree?(Take Height or level of root as one(1))
With this article at OpenGenus, you must have the complete idea of Bottom view of a Binary Tree.
