
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we have explained efficient algorithms to Find all anagrams of a given string. This involve techniques like sliding window approach.
| Table of Contents |
|---|
| 1)Problem statement |
| 2)Naive approach |
| 3)Sliding Window approach |
| 4)Conclusion |
An anagram of a word is that which is formed by rearranging the letters of the word in some order.
For example,
Some of the anagrams of the word "abcd" are "abdc","bdac","cabd","acdb"....
1)Problem statement
Given two strings s1 and s2. Find all anagrams of the string s2 in s1.
For example,
Let s1="cbdcbcacbdbcac" s2="abcc"
cbd[cbca]cbdbcac
cbdc[bcac]bdbcac
cbdcb[cacb]dbcac
cbdcbcacbd[bcac]
Hence the anagrams of s2 in s1 are highlighted above.
2)Naive approach
Let 'n' be the length of string s1 and 'k' be the length of string s2.
In this approach we'll consider each substring of string s1 and check whether the substring is an anagram of string s2.
Implementation
#include <bits/stdc++.h>
using namespace std;
//check if the character counts are the equal or not
bool isEqual(int charCount1[],int charCount2[])
{
for(int i=0;i<26;i++)//iterate through 26 characters
{
//even if one character count is not
//equal then the strings can't be anagrams
if(charCount1[i]!=charCount2[i])
{
return false;//in such case return false
}
}
//if the character counts are equal then return true
return true;
}
int main()
{
string s1="cbdcbcacbdbcac",s2="abcc";
//the res vector stores the starting indices
//of substrings(length 'k') of s1 that are anagrams of s2
vector<int> res;
//store the character counts in arrays
//for 'a' index is 0,'b' index is 1,'c' index is 2,...,'z' index is 25
int charCount1[26],charCount2[26];
//intially fill the character counts with zeros
memset(charCount2,0,sizeof(charCount2));
//iterate through s2 and store the character counts
for(auto x:s2)
{
//x is a character of s2
//subtracting with 'a' gives the index
charCount2[x-'a']++;
}
int n=s1.size(),k=s2.size();
//iterate through each character of string s1
for(int i=0;i<n;i++)
{
//check if a substring exists of length 'k'
//starting from index 'i'
if(i+k-1<n)
{
//fill the character counts with zeros as
//for each substring the character count is counted seperately
memset(charCount1,0,sizeof(charCount1));
for(int j=i;j<i+k;j++)
{
//for each character encountered increment its count
charCount1[s1[j]-'a']++;
}
//check if the character counts of s2 and the
//substring of s1 of length 'k' starting with index 'i'
if(isEqual(charCount1,charCount2))
{
//if character counts are equal then append
//the starting index 'i' of the substring to the result
res.push_back(i);
}
}
}
//display the starting indices of substrings of length
//'k' belonging to string s1 which are anagrams of s2
for(auto x:res)
{
cout<<x<<" ";
}
return 0;
}
3 4 5 10
Let's calculate the time complexity of this approach...
Iterate through string s1 - O(n)
For each index 'i' considering it as the starting index find a substring of length 'k' - O(n*k)
For each substring check if it can be an anagram of s2 i.e., iterate through 26 alphabets - O(n*k*26), 26 is a constant and can be ignored.
Hence,the time complexity of the naive approach is O(n*k).
The time complexity can be improved through optimized approach.
Let's look at the sliding window approach.
3)Sliding Window approach
The sliding window approach is a slight modification of the naive approach, the character counts of the subtrings are calculated in constant time.
Here, we maintain a window based on given constraints and move the window incrementally.
The constraint here is to find substring of length 'k'.Hence, we maintain a window of size 'k'.
As charCount is an array of size 26 it is difficult to represent it.Hence, the indices which will have count>0 will be shown.
Let's suppose you have calculated the character count of the substring with ending index as '3'.
b-1,c-2,d-1
charCount1->[1:1,2:2,3:1]

What will be the character count of the substring with ending index as '4' and is of length 'k'?
The answer can be obtained through the previously calculated window.
Reduce the character count of character at index 'i-k' by one and Increase the character count of character at index 'i' by one. This will be the new window.
It will be calulated as follows
charCount1[s1[i-k]-'a']-- , charCount1[s1[i]-'a']++
charCount1[s1[4-4]-'a']-- , charCount1[s1[4]-'a']++
charCount1[s1[0]-'a']-- , charCount1[s1[4]-'a']++
charCount1['c'-'a']-- , charCount1['b'-'a']++
charCount1[2]-- , charCount1[1]++
b-2,c-1,d-1
charCount1->[1:2,2:1,3:1]
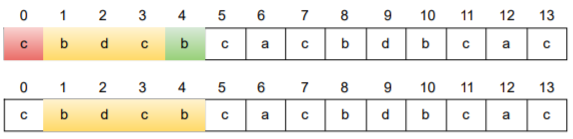
Similarly, what will be the character count of the substring with ending index as '5' and is of length 'k'?
It will be calulated as follows
charCount1[s1[i-k]-'a']-- , charCount1[s1[i]-'a']++
charCount1[s1[5-4]-'a']-- , charCount1[s1[5]-'a']++
charCount1[s1[1]-'a']-- , charCount1[s1[5]-'a']++
charCount1['b'-'a']-- , charCount1['c'-'a']++
charCount1[1]-- , charCount1[2]++
b-1,c-2,d-1
charCount1->[1:1,2:2,3:1]
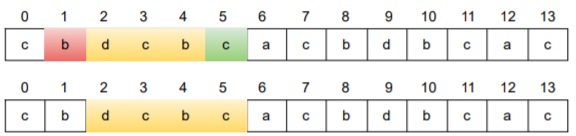
In similar way, the character counts for each substring of length 'k' can be calculated.
Algorithm
1.Create two character counts arrays(charCount1,charCount2) of size 26 each
2.Store the character counts of string s2 in charCount2
3.Iterate through first k characters of string s1 and store the character counts in charCount1
4.If the character counts are equal(charCount1=charCount2) then append index 0 to the result
5.Iterate through the remaining characters,say iterating index is i
5.1.The substring to be considered is the one ending with index i and is of length k that means the starting index is i-k+1
5.2.Decrement the character count of character at index i-k by one
5.3.Increment the character count of character at index i by one
5.4.Now the character counts array of s1 (charCount1) will have the character counts of the substring with starting index as i-k+1 and ending index as i
5.5.If the character counts of s2 and s1 are equal (charCount1=charCount2) then append index i-k+1 to the result
Let's look at the dry run for few initial substrings.
charCount2->[0:1,1:1,2:2]
First k characters
b-1,c-2,d-1
charCount1->[1:1,2:2,3:1]

Ending index-4
charCount1[s1[i-k]-'a']-- , charCount1[s1[i]-'a']++
charCount1[s1[4-4]-'a']-- , charCount1[s1[4]-'a']++
charCount1[s1[0]-'a']-- , charCount1[s1[4]-'a']++
charCount1['c'-'a']-- , charCount1['b'-'a']++
charCount1[2]-- , charCount1[1]++
b-2,c-1,d-1
charCount1->[1:2,2:1,3:1]

Ending index-5
charCount1[s1[i-k]-'a']-- , charCount1[s1[i]-'a']++
charCount1[s1[5-4]-'a']-- , charCount1[s1[5]-'a']++
charCount1[s1[1]-'a']-- , charCount1[s1[5]-'a']++
charCount1['b'-'a']-- , charCount1['c'-'a']++
charCount1[1]-- , charCount1[2]++
b-1,c-2,d-1
charCount1->[1:1,2:2,3:1]

Ending index-6
charCount1[s1[i-k]-'a']-- , charCount1[s1[i]-'a']++
charCount1[s1[6-4]-'a']-- , charCount1[s1[6]-'a']++
charCount1[s1[2]-'a']-- , charCount1[s1[6]-'a']++
charCount1['d'-'a']-- , charCount1['a'-'a']++
charCount1[3]-- , charCount1[0]++
a-1,b-1,c-2
charCount1->[0:1,1:1,2:2] (charCount1=charCount2) starting_index=6-4+1=3 res=[3]

Ending index-7
charCount1[s1[i-k]-'a']-- , charCount1[s1[i]-'a']++
charCount1[s1[7-4]-'a']-- , charCount1[s1[7]-'a']++
charCount1[s1[3]-'a']-- , charCount1[s1[7]-'a']++
charCount1['c'-'a']-- , charCount1['c'-'a']++
charCount1[2]-- , charCount1[2]++
a-1,b-1,c-2
charCount1->[0:1,1:1,2:2] (charCount1=charCount2) starting_index=7-4+1=4 res=[3,4]

In this way the process continues...
Implementation
#include <bits/stdc++.h>
using namespace std;
//check if the character counts are the equal or not
bool isEqual(int charCount1[],int charCount2[])
{
for(int i=0;i<26;i++)//iterate through 26 characters
{
//even if one character count is not
//equal then the strings can't be anagrams
if(charCount1[i]!=charCount2[i])
{
return false;//in such case return false
}
}
//if the character counts are equal then return true
return true;
}
int main()
{
string s1="cbdcbcacbdbcac",s2="abcc";
//the res vector stores the starting indices
//of substrings of s1 that are anagrams of s2
vector<int> res;
//store the character counts in arrays
//for 'a' index is 0,'b' index is 1,'c' index is 2,...,'z' index is 25
int charCount1[26],charCount2[26];
//intially fill the character counts with zeros
//the charCount1 array will be filled with zeros only once and the character counts
//of each substring is calculated in constant time through some modification
memset(charCount1,0,sizeof(charCount1));
memset(charCount2,0,sizeof(charCount2));
//iterate through s2 and store the character count
for(auto x:s2)
{
//x is a character of s2
//subtracting with 'a' gives the index
charCount2[x-'a']++;
}
int n=s1.size(),k=s2.size(),i;
//iterate through first 'k' characters of string s1
i=0;
for(;i<k;i++)
{
charCount1[s1[i]-'a']++;
}
//if the substring starting with index '0' and is of length 'k'
//then add that index to the result
if(isEqual(charCount1,charCount2))
res.push_back(0);
//iterate through the remaining characters of string s1
for(;i<n;i++)
{
//substring to consider is from index 'i-k+1' to 'i' which will be of length 'k'
//decrement the character count of the character at index 'i-k' as
//the character at that index will not be included for the substring considered
charCount1[s1[i-k]-'a']--;
//increment the character count of the character at index 'i' as
//the character will be the last for the substring considered
charCount1[s1[i]-'a']++;
//check if the character counts of substring ending with
//index 'i' of length 'k' and s2 are equal or not
if(isEqual(charCount1,charCount2))
{
//if character counts are equal the append the starting index of the substring to the result
//if the ending index of the substring of length 'k' is 'i' then starting index would be 'i-k+1'
res.push_back(i-k+1);
}
}
//display the starting indices of substrings of length
//'k' belonging to string s1 which are anagrams of s2
for(auto x:res)
{
cout<<x<<" ";
}
return 0;
}
3 4 5 10
Let's calculate the time complexity of this approach...
Iterate through string s1- O(n)
For each substring ending with index 'i' and is of length 'k' check if it can be an anagram of s2 i.e., iterate through 26 alphabets - O(n*26), 26 is a constant and can be ignored.
Hence the overall time complexity is O(n).
4)Conclusion
Hence, through the sliding window approach the time complexity is reduced from O(n*k) to O(n).
With this article at OpenGenus, you must have the complete idea of how to Find all anagrams of a given string.
