Find Nth lexicographic permutation of string

Problem Statement

Given a string of length of m containing only lowercase alphabets. Find out the lexicographic nth permutation of the given string.

For example:

If given string, s = "abc", find 3rd permutation

permutations of "abc" are:
1. abc
2. acb
3. bac
4. bca
5. cab
6. cba

So, the third permuation of will be "bac".

Use Recursion and Backtracking to solve

---

In this approach we find all the distinct permutations of the given string using recursion. Once permutations are found, we sort the permutations if it is not already sorted and then return the (n-1)th permutation as we will use zero based indexing.

Before moving ahead, let's first understand the concept of permutation in mathematics. In mathematics the permutation of a set is nothing but the number of ways the elements of the set can be arranged so that no two arrangements are identical.
For instance - if the given set is {2, 3}, there are two ways in which it's elements can be arranged, first-{2, 3} and second-{3,2}.

Key Observations

• If the set has all distinct elements then the number of ways the elements can be arranged is n!(n factorial).
• If there are n elements and we have to arrange it into r places, where n < r then the permutation will be nPr = n!/(n-r)!.
• If there are n elements to be arranged in n places and has one element duplicated m times then the permutation will be n!/m!.

Steps to the solution

1. Find all the permutations of the given string and store it into a data structure
2. If the permutation algorithm does not return sorted permutation, sort the permutations
3. Return the the (n-1)th element of the permutations, if zero based indexing has been used and that we will.

Algorithm to find all the distinct permutations

start procedure getPermutations: str
	Map m
	for each element in str
		m[element] = m[element] + 1

	List list
	getPermutations(m, "", list, str.length, 0)
	return list
end procedure

start procedure getPermutations: map, ans, list, n, idx
	if idx == n:
		list.add(ans)
		return

	for each key in map.keySet():
		if m[key] > 0:
			m[key] -= 1
			getPermutations(map, ans + key, list, n, idx + 1)
			m[key] += 1 //backtrack
end procedure

Let us take again the example of finding permutations of string "abc". Here's how the recursion tree will look like for the above mentioned algorithm.

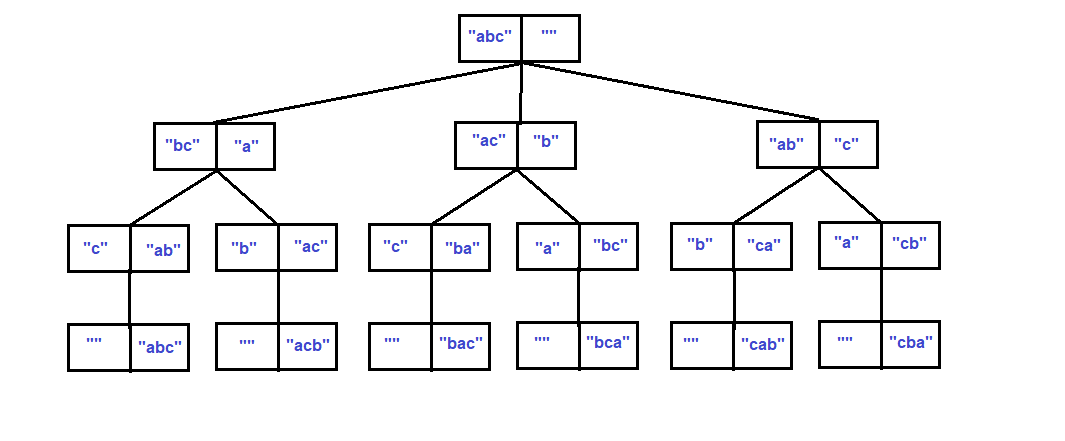
Java Implementation to find nth permutation

import java.util.ArrayList;
import java.util.HashMap;

public class StringPermutation {
    private static void getPermutation(HashMap<Character, Integer> str, String ans, ArrayList<String> perm, int n, int i) {
        if(i == n) {
            perm.add(ans);
            return;
        }
        
        for(Character ch: str.keySet()) {
            if(str.get(ch) > 0) {
            	str.put(ch, str.get(ch) - 1);
            	getPermutation(str, ans + ch, perm, n,i + 1);
            	str.put(ch, str.get(ch) + 1);
            }
        }
    }
    
    public static ArrayList<String> getPermutation(String str) {
    	HashMap<Character, Integer> characters = new HashMap<Character, Integer>();
    	for(int i = 0;i < str.length();++i) {
    		characters.put(str.charAt(i), 0);
    	}
    	
    	for(int i = 0;i < str.length();++i) {
    		characters.put(str.charAt(i), characters.get(str.charAt(i)) + 1);
    	}
    	
    	ArrayList<String> list = new ArrayList<>();
        getPermutation(characters, "", list, str.length(), 0);
        
        return list;
    }

    public static void main(String[] args) {
        String str = "aabc";
        int n = 3;
        ArrayList<String> permutations = getPermutation(str);

        System.out.println(permutations.get(n - 1));
    }
}

Time Complexity

As we are finding all the permutations of the given string, it takes O(n!) time to do so as string can have n! permutations. Again we are traversing all the characters of the string which takes O(n) time. So, the total time complexity of the algorithm will be O(n * n!).

Space Complexity

We are using HashMap to store all the characters of the string which takes O(n) space as the string has n characters and again we are storing all the permutations of the string into array list which takes O(n!) space as the string has n! permutations.
So, the total space complexity of the algorithm will be O(n + n!) or O(n!).

The Efficient Approach

There's a way to find the nth permutation of a string without finding all the permutation. Yes! We can directly find out the nth permutation of the string. There's only one constraint, the string should be sorted.

Let us take an example and solve it step by step to understand the proccess of finding it. Let's say we have the string "abcd" and we have to find out the 17th permutation of the string.

We know that total number of permutations will be 24. Now, let's use our brain here. We know that the permutation involves only four letters- a,b,c and d and it could start with any of it. So,

If permutation starts with a:
    Other letters are permutationsOf(bcd) (0th - 5th)
If permutation start with b:
    Other letters are permutationsOf(acd) (6th - 11th)
If permutation start with c:
    Other letters are permutationsOf(abd) (12th - 17th)
If permutation start with d:
    Other letters are permutationsOf(abc) (18th - 23th)

Looking at the above intervals we can easily find out that permutation lies between 12th to 17th permutation i.e. starts with c.

Now, that we know that our permutation starts with c and lies between 12th to 17th range,which is a total of 6 permutations, we need to find which permutation in this interval is the 17th permutation. Since 12 permutations has already been discarted we get it by doing 17%6, which is 5. It means we have to find the 5th permutation of string abd.

Here's the possibilities:

If the permutation starts with a:
    Other letters in the permutation are permutationsOf(bd)(0th - 1th)
If the permutation starts with b:
    Other letters in the permutation are permutationsOf(ad) (2nd to 3rd)
If the permutation starts with d:
    Other letters in the permutation are permutationsOf(ab) (4th - 5th)

Again, we can easily find that our 5th permutation lies in the range 4th to 5th. So, the second letter of the permutation will be d.

To find the third letter in the permutation, we will have to find the the 5%2th or 1st permutation in the interval. Which is again

If the permutation starts with a:
    Other letters in the permutation are permutationsOf(b)(0th)
If the permutation starts with b:
    Other letters in the permutation are permutationsOf(a)(1st)

Here, we find that our permutation starts with b. So, the third letter in our permutation will be b.

Again, we follow the same steps to find the 1%1th i.e. 0th permutation of a, which is nothing but a.

So, the fourth letter in our permutation will be a.
And we get our 17th permutation as "cdba".

Once you have understood the above example, you can quicky come up with the steps required to solve the problems. Here are the steps we take to solve the problem

Step 1: Make a variable fact and initilize it to 1.
Step 2: Find the factorial of length of string minus 1 and store it into fact.
Step 3: Make a variable ans of type String and initialize it to an empty string.
Step 4: Get the character from the given string at index (n/fact), where n is the index of permutation to be found. n is already provided to us in the problem statement.
Step 5: Delete the character from the string at index n / fact.
Step 6: Check if the length of the string is 0 and if it is then stop the processing.
Step 7: Set the value of n to n % fact.
Step 8: Set the value of fact to fact / s.length(), where s.length() is size of string after deleting a character.
Step 9: Repeat the steps from step 4 till 8 until the size of the string becomes 0.
Step 10: Return the value of ans.

Java Implementation

public class Solution {
    public static String getPermutation(String str, int n) {
        int size = str.length();
        int fact = 1; // used to find the starting letter of nth permutation of the string
        
        for(int i = 1;i < size;i++) {
            fact = fact * i;
        }
        
        StringBuilder s = new StringBuilder(str);
        String ans = "";
        
        while(true) {
            ans = ans + s.charAt(n / fact);
            s.deleteCharAt(n / fact);
            if(s.length() == 0)
                break;
            
            n = n % fact;
            fact = fact / s.length();
            // we can utilize size variable here as fact = fact / (size = size - 1);
        }
        
        return ans;
    }
    
    public static void main(String[] args) {
        String abc = "abcd";
        System.out.println(getPermutation(abc, 16));
    }
}

Time and Space complexity

Here we can clearly see that we are able to find the letter at a position in each iteration. So, to if the length of string is n we need n iterations to find all the characters in the given permutation. So, the time complexity of this approach is O(n). The same way here I have used a StringBuilder to store the character sequence which again takes O(n) space complexity.

That's it for this article at OpenGenus.
Happy Coding.
See you.