In this article, we have presented an algorithm to Find permutations of string in lexicographic order. We have used the concept of Recursion.

Table of contents:

1. What is lexicographic order of a string?
2. What is permutation?
3. Using recursion to find the lexicographic order
4. Implementation
5. Time and Space Complexity

What is lexicographic order of a string?

Lexicographic order of a string is the set of strings in the order in which they would appear in the dictionary had all the permutations being part of the dictionary.
For e.g.:- Suppose the string given is CBA, then its lexicographic order will be ABC, ACB, BAC, BCA, CAB, CBA in their respective orders.

What is permutation?

Permutations of a string(or a set of characters) is the set of all the strings which can be made by arranging the characters of string in all the different ways possible.

For e.g. :- For a given string PQR, the various ways in which it can be arranged will PQR itself, PRQ, RPQ, RQP, QPR, QRP.

Using recursion to find the lexicographic order

We use the idea of divide and conquer to solve this problem.
In which we reduce the size of the string for which we need to find the permutations in lexicographic order until we get reduced to our base case and then returm from there and adding the strings which were spliced down to produce the permutations.

Algorithm:-

1. Take any string as an input.
2. Sort the string.
3. Pass the sorted string to our permute function.
4. Splice the string into two parts, one part having a single character and other part having the remaining part of the string.
5. Once again recur the remaining part of string as the string for which permutations are needed to be found.
6. Repeat step 4, till we don't get a string of only a single character. In that case, return the single character.
7. Concatenate the spliced part to the returned single character, and append it to the array keeping track of permutations.
8. Now, concatenate the spliced part to the corresponding substrings present inside permuted_array.
9. Repeat the algorithm for every character as a spliced part.
10. Final array will be our lexicographic order of permutation.

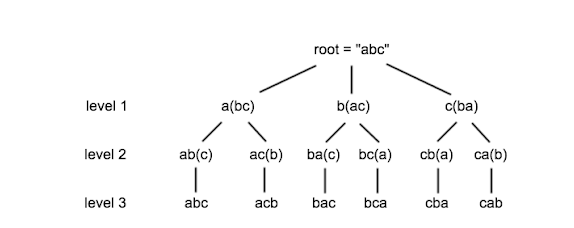
In the image the example of finding permutations of string "abc" is given where we have used the recursion tree to visualise this algoithm, as can be seen, firstly we have separated out the characters a, b and c respectively to get the remaining strings and then in the second stage we have again did the same thing by separating the remaining characters and then reaching a stage where our string is of unity length, after which we return backwards and on the backwards journey we simply concatenate the characters which we had broken to get the permutation for that string.

Example:-

For example:- In the case of abc, at the first step of recursion, we have sliced out a and (bc).
After which our string has been reduced to "bc".(which will be our input to the same recurring function iteratively).
Now, further on the second stage we reduce the strings of length two into strings of unit length namely "b" and "c".
Now on our path to backwards we got "b" and "c", when we spliced out "c" and "b" respectively, thus, again concatenating "c" and "b" to "b" and "c" we get "bc" and "cb" and appending them to our permuted_array in that order.
Now, our permuted_array contains ["bc","cb"] , which is the result when we spliced out "a" from the original string and transferred "bc" as input to our recurrence function, thus, concatenating "a" to "both the elements of permuted_array we get ["abc", "acb"].
We will do the similar procedure in the next iteration by splicing out "b" from "abc", and transferring the input "ac" to the recursive function which in turn will modify our permuted_array to ["abc", "acb", "ac", "ca"], to which we concatenate "b", (we will concatenate "b" to only "ac", and"ca") to get ["abc", "acb", "bac", "bca"].
We will do the similar procedure in the next iteration by splicing out "c" from "abc", and transferring the input "ab" to the recursive function which in turn will modify our permuted_array to ["abc", "acb", "bac", "bca","ab","ba"], to which we concatenate "c", (we will concatenate "c" only to only "ab", and"ba") to get ["abc", "acb", "bac", "bca","cab","cba"].

Similar, procedures can be done for strings of length 4, 5 ,etc.

Implementation:-

Following is the implementation in Python:

# permuted_array is our list to store the permutations in lexicographic order
global permuted_array 
permuted_array=[]
#count is our array to store the index for permutations of various length. 
global count
#function to calculate the permutations.
def permute(remaining):
    if len(remaining)==1:
        return remaining
    for i in range(0,len(remaining)):
    #We splice the strings to get substrings which further will be reduced.
        string=remaining[0:i]+remaining[i+1:len(remaining)]
    #Recurring the spliced string to generate shorter strings.
        permuted=permute(string)
    # Base case.
        if(len(permuted)==1):
    # Concatenate the strings 
            permuted_array.append(remaining[i]+permuted)
        else:
            j=len(permuted_array[-1])#To find the length of the shortest length string in the permuted_array at any given time as modifications will be done to only those strings.
            for k in permuted_array:
                if(len(k)!=j):
                    continue
                else:
     #Concatenating the required substrings.
                    permuted_array[count[len(remaining)-1]]=remaining[i]+permuted_array[count[len(remaining)-1]]
                count[len(remaining)-1]+=1
    return permuted_array
test_string=input("Enter the string")
#sorting the input string, as only then we will be able to find out the lexicographic order using this algp, otherwise it will just print permutations irrespectove of lexicographic order.
string = ''.join(sorted(test_string))
count=[len(string)]
for i in range(0,len(string)):
    count.append(0)
permute(string)
print(permuted_array)

Time and Space Complexity:-

Time complexity is O(n n!)*, as our time complexity will be of the form T(n)= n! + n* n! + (n-1)* (n-1)! + (n-2)* (n-2)! +... 1! , which will amount to T(n)= n! + (n+1)! -1! , as n* n! + (n-1)* (n-1)! + (n-2)* (n-2)! +... 1! = (n+1)! -1!. Thus, T(n) = n! + (n+1)! = n!+ (n+1)* n! = n* n! + 2* n!.
Thus, T(n) = n * n!.
Space complexity is O(n!) as we require an array to store all the permutations.

With this article at OpenGenus, you must have the complete idea of how to Find permutations of string in lexicographic order.