Approximate String Matching

Introduction

In the era of vast data repositories, retrieving accurate textual information can be challenging, especially in the presence of errors or imprecise queries. To address this challenge, approximate string matching techniques offer a powerful solution.
In computer science, approximate string matching involves seeking strings in a text that closely resemble a specified pattern. In simpler terms, it's a method of searching for text matches, even when users input words with errors or provide incomplete search terms. In this article at OpenGenus.org, we have explored Approximate String Matching.

This capability, often referred to as fuzzy string searching, finds widespread utility in diverse domains such as search engines, databases, spell checkers, plagiarism detectors, and more.

For instance, when designing multi-stage filters within database management systems, one crucial stage involves conducting approximate string comparisons. This step plays a pivotal role in identifying duplicate records by assessing the similarity of strings. Notably, the effectiveness of this process hinges on the judicious selection of string identity criteria and the choice of suitable comparison algorithms.

Approximate String Matching methods

The main idea of approximate string matching methods is to enable the user to determine that two texts (or sets of data as a whole) are completely or at least partially similar to each other.

To study methods for approximate string matching, it is necessary to first describe the concepts of measure and metric of a string.

String-based measures work with string sequences and character composition.
In mathematics and computer science, a string metric (also known as a string similarity metric or string distance function) is a metric that measures the distance ("inverse similarity") between two text strings for approximate matching or string comparison and in fuzzy string searches.

The following approaches are used to determine string similarity

1. Character-based.
2. Term-based.
3. Corpus-based.
4. knowledge-based.

The most popular and widely used in various applied problems are fuzzy string comparison methods based on the symbolic approach.
Let's consider these methods:

1. Damerau-Levenshtein method.

In information theory and computer science,Levenshtein distance is a string metric for measuring the difference between two sequences.
Otherwise known as edit distance, the Levenshtein distance is considered a way to quantify how dissimilar two strings (such as words) are by calculating the minimum number of operations required to transform one string into another.

2. Jaro-Winkler method
In computer science and statistics, Jaro-Winkler distance method is a measure of similarity between two strings.
The higher the Jaro distance for two strings, the greater the similarity between them.
It uses a prefix scale that gives more favorable scores for strings corresponding to a given prefix length at the beginning of the string.

Approximate string matching Algorithms

Approximate string matching algorithms fall under the category of string comparison algorithms.String comparison is a technique used to find the results of one or more specified text patterns.
Comparing strings is an important task in computer science because text is the primary form of information exchange between people, such as in literature, scientific papers, and web pages.
A string comparison algorithm is an algorithm for finding all occurrences of strings by searching for similarities.

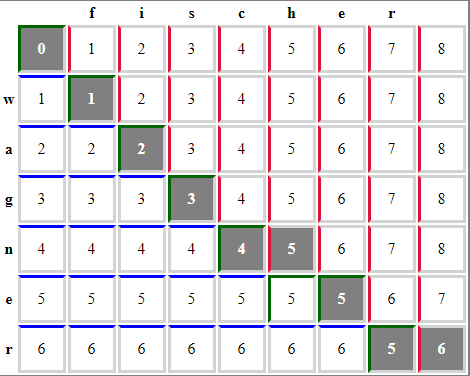
1. Wagner-Fisher algorithm
The Wagner-Fisher algorithm is a dynamic programming algorithm works by finding the minimum number of single-character edit operations (insertions, deletions, or substitutions) needed to transform one string into another using the Levenshtein method.
The Wagner-Fisher algorithm allows you to calculate the edit distance based on the observation that if you reserve a matrix to store the edit distances between all the prefixes of the first row and all the prefixes of the second, then you can calculate the values in the matrix by populating the matrix, and thus find the distance between two complete lines as the last calculated value.

Here's a JavaScript implementation of the Wagner-Fisher algorithm:

function levenshteinDistance(str1, str2) {
  const matrix = [];

  // Initialize the matrix
  for (let i = 0; i <= str1.length; i++) {
    matrix[i] = [i];
  }

  for (let j = 0; j <= str2.length; j++) {
    matrix[0][j] = j;
  }

  // Fill in the matrix
  for (let i = 1; i <= str1.length; i++) {
    for (let j = 1; j <= str2.length; j++) {
      const cost = str1[i - 1] === str2[j - 1] ? 0 : 1;
      matrix[i][j] = Math.min(
        matrix[i - 1][j] + 1, // Deletion
        matrix[i][j - 1] + 1, // Insertion
        matrix[i - 1][j - 1] + cost // Substitution
      );
    }
  }

  // The minimum edit distance is in the bottom-right cell of the matrix
  return matrix[str1.length][str2.length];
}

// Example usage
const distance = levenshteinDistance("wagner", "fisher ");
console.log(`Levenshtein Distance: ${distance}`);

2.Jaro-Winkler algorithm
The Jaro-Winkler distance algorithm is an algorithm using a string metric approach that performs string comparisons using appropriate mathematical functions.

It should be noted that the Jaro-Winkler algorithm is an algorithm for measuring the similarity between two strings, and most of this algorithm is used to detect duplication in strings.
The higher the Jaro-Winkler distance value for two strings, the higher the similarity of both strings.

Here's a JavaScript implementation of the Jaro-Winkler algorithm:

function jaroDistance(str1, str2) {
  const len1 = str1.length;
  const len2 = str2.length;

  if (len1 === 0 || len2 === 0) {
    return 0;
  }

  const matchDistance = Math.floor(Math.max(len1, len2) / 2) - 1;
  const matches = new Array(len1 < len2 ? len1 : len2).fill(false);
  let matchingCharacters = 0;

  for (let i = 0; i < len1; i++) {
    const start = Math.max(0, i - matchDistance);
    const end = Math.min(i + matchDistance + 1, len2);

    for (let j = start; j < end; j++) {
      if (!matches[j] && str1[i] === str2[j]) {
        matches[j] = true;
        matchingCharacters++;
        break;
      }
    }
  }

  if (matchingCharacters === 0) {
    return 0;
  }

  let transpositions = 0;
  let j = 0;

  for (let i = 0; i < len1; i++) {
    if (matches[j]) {
      while (!matches[j]) j++;
      if (str1[i] !== str2[j]) transpositions++;
      j++;
    }
  }

  const jaroSimilarity = (matchingCharacters / len1 + matchingCharacters / len2 + (matchingCharacters - transpositions) / matchingCharacters) / 3;

  return jaroSimilarity;
}

function jaroWinklerSimilarity(str1, str2) {
  const jaroScore = jaroDistance(str1, str2);
  const prefixScale = 0.1; // Adjust this scaling factor as needed (typically between 0 and 0.25)

  // Calculate the common prefix length (up to a maximum of 4)
  let prefixLength = 0;
  while (prefixLength < 4 && str1[prefixLength] === str2[prefixLength]) {
    prefixLength++;
  }

  // Apply the Jaro-Winkler adjustment
  const jaroWinklerScore = jaroScore + prefixLength * prefixScale * (1 - jaroScore);

  return jaroWinklerScore;
}

// Example usage:
const string1 = "maximum";
const string2 = "minimum";
const similarity = jaroWinklerSimilarity(string1, string2);
console.log(`Jaro-Winkler similarity between "${string1}" and "${string2}": ${similarity}`);

OUTPUT:
Jaro-Winkler similarity between "maximum " and "minimum": 0.7417857142857143

Conclusion

Approximate string matching is a fundamental technology that underpins various applications, making it indispensable in the modern data-driven world. By understanding the methods and algorithms discussed in this article, developers and data scientists can harness the power of approximate string matching to improve search accuracy, data quality, and information retrieval across a wide range of domains. As data continues to grow in complexity and volume, the importance of these techniques will only continue to expand, ensuring that accurate textual information remains accessible and useful.