
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we have explored the strategy to implement Binary Tree in Python Programming Language with complete explanation and different operations like traversal, search and delete.
Table of contents:
- Basics of Binary Tree
- Implementation in Python with Explanation
- Traversal operation
- Search Operation
- Deletion operation
Basics of Binary Tree
What is Binary Tree?
Binary tree is special type of heirarichal data structures defined using nodes. Basically its extended version of linked list. Its a tree data structure where each node is allowed to have maximum two children node, generally referred as Left Child and Right Child. Hashing, routing data for network traffic, data compression, and binary search trees are some of its application.
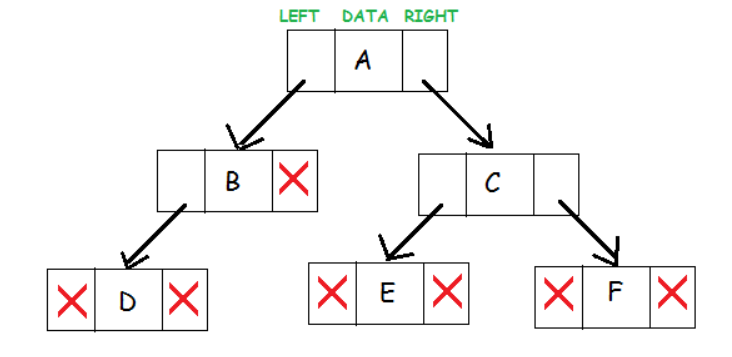
Data, left subtree and right subtree are three important features in a binary tree. Each data resides in the Data cell with left pointer pointing to subsequent left subtree and Right Data cell with right pointer pointing to subsequent eight subtree.
**Some Key Termniogies:- **
Root:- The Topmost node
Height:- Total Number of edges from root node to last(deepest) node
Leaf:- Node with no children
Depth of a Tree: The number of edges from the tree’s node to the root is.
Internal Node:- Node having atleast one Children
Type of Binary Tree
- Perfect Binary Tree
A Binary Tree with all the interior node (all nodes except leaf node) have two children and all leaf node has same depth
- Balanced Binary Tree
Every tree where the maximum difference between right and left subtree height is 1.
3)Complete Binary Tree
All binary tree where every node is completly filled with 2 or 0 node .
4)Degenrate Binary Tree
Every binary tree, where every internal node has only single child.
Applications of Binary Tree
- Used in 3d Video Games.
- Highly used in router for tabling purpose.
- Scheduling processes in OS.
Implementation in Python with Explanation
Implementing the Code :-
class BinaryTree:
def __init__(self, value):
self.left = None
self.right = None
self.value = value
def insert(self, value):
if self.value:
if data < self.value:
if self.left is None:
self.left = BinaryTree(value)
else:
self.left.insert(value)
elif data > self.value:
if self.right is None:
self.right = BinaryTree(value)
else:
self.right.insert(value)
else:
self.value = value
def PrintTree(self):
if self.left:
self.left.PrintTree()
print( self.data),
if self.right:
self.right.PrintTree()
root = BinaryTree(100)
root.insert(50)
root.insert(55)
root.insert(60)
root.insert(20)
root.insert(52)
root.PrintTree()
Ouput:- 20,24,35,40,55,60
Structure Of the Tree :-
40
/ \
35 55
/ \
20 60
\
24
**Explanation:- **
Here, we define a class BinarTree, in which 3 methods are defined
__init__- insert()
- PrintTree()
__init__ methods are self called.
Now in the main funcion as we create a object of class in root, we pass the value 40, which we want to be the root element. In the next line we call insert() method with the object and pass the value 35, which take the flow of program to insert function, there we check if the new value is greater or less then its parent value with (if value<self.value and it counterpart), here 35<40 so the flow goes to another if condition and check is the self.left value is empty or not. If it empty which in this case is, updates the value of self.left and also update the self.value to 35.
40
/
35
Now we call the insert function with value 55, the same process as prescribed above goes here also, but here 50>35(since previously self.value was updated using self.left=BinaryTree(35) and 50 is the new value), so the flow goes to elif condition under which it see self.right is indeed equal to None therefore it updates it to 55 and self.value to 55.
40
/ \
35 55
Similarly, the rest of insert function are called and executing on every value the final Binary tree is obtained.
Traversal operation
When, we print the values of every node here we are using preorder traversal where left first left most child is printed, then root, then the right child.
Traversal:-
- PreOrder Traversal
- InOrder Traversal
- PostOrder Traversal
PostOrder Traversal:-
Here the Left child is visited first, then the Right child node and then Root node.
The minutes changes in the PrintTree() method is following
def PrintTree(self):
if self.left:
self.left.PrintTree()
if self.right:
self.right.PrintTree()
print(self.value)
Output:- 24,20,35,60,55,40
PreOrder Traversal
Here the Root is visited first, then left child node and then right child node.
The minutes changes in the PrintTree() method is following
def PrintTree(self):
print(self.value)
if self.left:
self.left.PrintTree()
if self.right:
self.right.PrintTree()
Output:- 40,35,20,24,55,60
Search Operation
Searching in a Binary Tree
Searching in a binary tree is a very simple step, as we have already discussed traversing a binary tree, so we can use the traversing technique to get all the elements in a tree and and find our required element. Here we are using preorder traversal, you guys can use anyone of them.
def PrintTree(self,element):
if self.left:
self.left.PrintTree()
if(self.data==element):
print("Found",self.data)
return(1)
else:
continue
if self.right:
self.right.PrintTree()
Deletion operation
Deleting a element from the binary tree
def delete_Node(root, key):
if not root:
return root
if root.val > key:
root.left = delete_Node(root.left, key)
elif root.val < key:
root.right= delete_Node(root.right, key)
else:
if not root.right:
return root.left
if not root.left:
return root.right
temp_val = root.right
mini_val = temp_val.val
while temp_val.left:
temp_val = temp_val.left
mini_val = temp_val.val
root.right = deleteNode(root.right,root.val)
return root
Explanation
The above programs explain the procedure to delete a particular element from the given binary tree. Here root represents the root node and key represents the element that needs to be deleted or has been ordered by the user.4
--> Searching for key element in either left or right subtree
Initially it checks wether the root(the topmost element ) is empty or not, if its not empty then it check the key element is less then the root element, if it holds true the the curosr searchers in the left subtree of the main tree, else it searches in the right subtree.
--> Examining the key node after finding it and then finally deleting it
In the else condition with condition if not root.right it checks if theres no right children for the node (key) and the new node is root node itself, and with the condition if not root.left it chekcs if there is no left children to delete then root node itself is the node.
Now if the both left and right children exist for the key node that is to be deleted then, we replace the key node with minimum value of its right subtree and then delete that minimum node in that right subtree.
With this article at OpenGenus, you must have the complete idea of Implementing Binary Tree in Python Programming Lanuguage.
