In this article, we have explored the approach of Boundary Traversal of Binary Tree along with Time and Space Complexity.

Contents:

• Introduction
• Implementation
• Result
• Complexity

Introduction

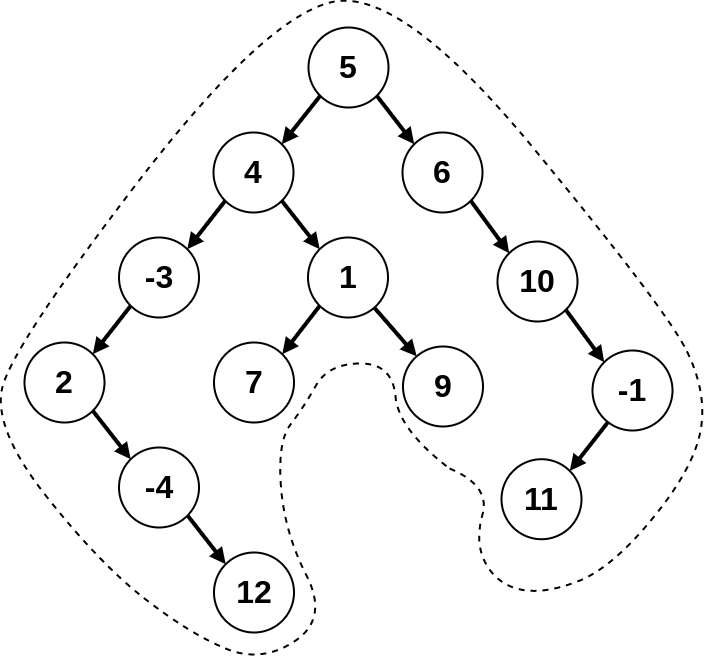
When we capture only elements that exist on the Boundary of the Binary Tree is the kind of traversing, is what "Boundary Traversal of Binary Tree" refers to.

For example:

We can collect three following types of nodes:

1. (1&2) left end nodes and right end nodes

These are the nodes that you can see on every level, and on every level they exists on the very beginning of the level or on the very end of the level, if we take above diagram as an example, then,

Left end nodes: [5, 4, -3, -2, -4, 12]
Right end nodes: [5, 6, 10, -1, 11]

3. leaf nodes

Any node that has no child will be considered as a leaf nodes. So, again if we take above diagram as reference, then,

Leaf nodes: [12, 7, 9, 11]

Traversing of Binary Tree can be done in two manners,

• clock-wise

and

• anti-clockwise.

For clockwise first, we collect all the right end nodes and then the leaf nodes while reading it from right-to-left and then all the left end nodes from the bottom leaf node to the root of the tree.

And in case of anti-clockwise Of course, we will implement clockwise traversing in exact reverse.
Or we could just reverse the result of clockwise traversing to get the result for anti-clockwise.

Note: In the result, we cannot have duplicate nodes, but we may have duplicate values.

For example, we cannot read the root node in both right end traverse and left end traverse. i.e. we would have to remove 5 from them, depending if we do clockwise or anti-clockwise.

Implementation

Node:

Of course, first we need a tree before we could traverse it. For that we can create a class Node, which will have three attributes for a

• value: which can store a value or a pointer to something, we will be storing unique values, so, we can represent both ideas at the same time.
• pointer to the left child And pointer to the right child.

Something like,

class Node:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None

    def is_leaf(self):
        return self.left is None and self.right is None

defining an extra method called is_leaf, just to make our code more readable.

Methods

Let's define some methods, to divide the work of traversing between them.

Reading left end nodes:

To read all left end nodes on each level. We can write a recursive method or a loop that will it's child, but we will priortize left child over right child and store them in a list or array or recommended would be linked list.

This way, we can visit left most child on every level and if in case, left child is None ( not available ) then we will visit the right child, because, in this case right child should act as the left most or to say left end child.

And one more requirement is to exclude both root and the last left end node, hence, root and left most leaf node. Why? because as we noted this above that we cannot have redundancy.

    def all_lefts(self):
        lefts = []
        node = self
        while True:
            if node.left is not None:
                node = node.left
            elif node.right is not None:
                node = node.right
            else:
                return lefts[:-1]
            lefts.append(node.val)

Here, return lefts[:-1] will exclude the leaf node that would be include in the 2^nd last iteration.
And, to exclude the root node, we are starting the checks on the child nodes, which will automatically do that.

if you want to break in 2^nd last iteration itself, you can replace else: with:

if node.is_leaf():
    return lefts

Reading right end nodes:

To read right end nodes, we will follow the exact same idea as above the only thing we need to change here is the priority for the right child node over the left child node and everything should work as expected.

    def all_rights(self):
        rights = []
        node = self
        while True:
            if node.right is not None:
                node = node.right
            elif node.left is not None:
                node = node.left
            else:
                return rights[:-1]
            rights.append(node.val)

Note: that we're visiting the only one child node and not the other, for which we're using if elif, but while reading leafs we will be using two seperate if statements.

reading leafs

When we want the result for anti-clockwise then the leafs should be read from left-to-right and for clockwise leafs should be read from right-to-left.
To capture leafs we can create a recursive function, in which we can prioritize visiting left child first for left-to-right result and can prioritize visiting right child first for right-to-left result.

reading leafs from left-to-right:

    def leafs_lr(self, leafs=[]):
        if self.is_leaf():
            leafs.append(self.val)
        if self.left is not None:
            leafs = self.left.leafs_lr(leafs)
        if self.right is not None:
            leafs = self.right.leafs_lr(leafs)
        return leafs

reading leafs from right-to-left:

    def leafs_rl(self, leafs=[]):
        if self.is_leaf():
            leafs.append(self.val)
        if self.right is not None:
            leafs = self.right.leafs_rl(leafs)
        if self.left is not None:
            leafs = self.left.leafs_rl(leafs)
        return leafs

Traversing Clockwise:

Now if we use above defined methods to Traverse Clockwise, then sequence to use them would be:

1. [self.val] => This will give us the root node, since, that's where we will be starting from.
2. self.all_rights() => To get the nodes from root node till right end node.
3. self.leafs_rl() => This will return from right end to left end node.
4. self.all_lefts()[::-1] => And here we're reversing the all_lefts, therefore, we will get the list of nodes from left end nodes to root.

And then we will add the above statements all together.

    def traverse_clockwise(self):
        return [self.val] + self.all_rights() + self.leafs_rl() + self.all_lefts()[::-1]

Traversing Anti-Clockwise:

We will follow the same Idea as above, but only in opposite direction, from which we get the following code:

    def traverse_anti_clockwise(self):
        return [self.val] + self.all_lefts() + self.leafs_lr() + self.all_rights()[::-1]

Well, Of course, one can do self.traverse_clockwise()[::-1] and will get the same result for self.traverse_anti_clockwise().

Result

Let's take the diagram we saw above as an example.

tree = Node(5)

# lefts
tree.left = Node(4)
tree.left.left = Node(-3)
tree.left.right = Node(1)
tree.left.right.left = Node(7)
tree.left.right.right = Node(9)
tree.left.left.left = Node(2)
tree.left.left.left.right = Node(-4)
tree.left.left.left.right.right = Node(12)

# rights
tree.right = Node(6)
tree.right.right = Node(10)
tree.right.right.right = Node(-1)
tree.right.right.right.left = Node(11)

Sorry! for the above verbosity.

And now if we use traverse_clockwise() and traverse_anti_clockwise() on tree we should get:

print(tree.traverse_clockwise())
print(tree.traverse_anti_clockwise())

Output:

[5, 6, 10, -1, 11, 9, 7, 12, -4, 2, -3, 4]
[5, 4, -3, 2, -4, 12, 7, 9, 11, -1, 10, 6]

Complexity

Time Complexity

Since, Binary Tree has some numbers of nodes, then let's its N number of nodes.
Now, the operations we performed on the Tree to get the answer, were,

1. lefts
2. rights
3. leafs

For lefts and rights, in every iteration, we go down a level in the tree, and there are $\log_2{N}$ number of levels in a Binary Tree.

For leafs, we recursively visit every node in the Binary Tree, and there are $N$ numbers of nodes.

According to above points the Time complexity should be $O(2\log_2{N} + N)$,
i.e.

$$O(N)$$

There could be a case when Binary Tree will consist of only two leaf nodes, for example, if we remove Node(1), Node(7) and Node(9) from the above example, then it should create such Binary Tree,
and in this kind of Binary Tree, the Time Complexity will become $O(\log_2{N})$

Space Complexity

As for space complexity, when we traverse the Binary Tree we do create a list of nodes found for three different operations

And, there can only exist $\log_2{N}$ numbers of lefts and rights, but for reading leafs, there can exist [1, N/2] of leaf nodes, therefore total space complexity for Boundary Traversing results to

$$O(N)$$

And again if we find only 2 leafs in a Binary Tree then the space complexity can also result in $O(\log_2{N})$.

And In the case of the Binary Tree which is only the root node, will have both Time and Space Complexity of $O(1)$.

With this article at OpenGenus, you must have the complete idea of Boundary Traversal of Binary Tree.