Instruction selection by tree-rewriting

Instruction selection involves choosing target-language instructions for each IR statement. In this article, we discuss how it can be done by a tree-rewriting process whereby tree patterns that correspond to machine instructions are used to tile a syntax tree.

Table of contents.

1. Introduction.
2. Tree-translation.
3. Tiling an input tree.
4. Pattern matching.
5. Generalized tree matching.
6. Summary.
7. References.

Introduction.

Instruction selection is a large combinatorial task for machines rich in addressing modes e.g CISC or for machines with special-purpose instructions i.e for signal processing.

Instruction selection remains a large combinatorial task even if we assume the order of evaluation is given and that registers are allocated by a separate mechanism.

In this article, we look at instruction selection as a tree rewriting problem.
Although better code can be obtained for some machines using DAG's, tree representations of target instructions have been used effectively to construct the instruction-selection phase of a code generator from a high-level specification of the target machine. This is because DAG matching is far more complex than tree matching.

Tree-translation.

We use a sequence of trees at the semantic level as input to the code-generation process.
The trees are what we get after inserting run-time addresses into the intermediate representation, their leaves will have information about the storage types of their labels.

An example:
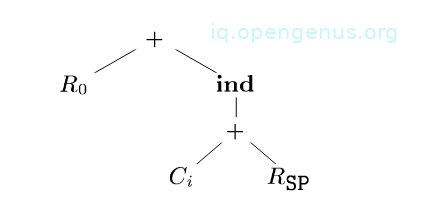
We have the following intermediate code tree for a[i] = b + 1.
[image 1]

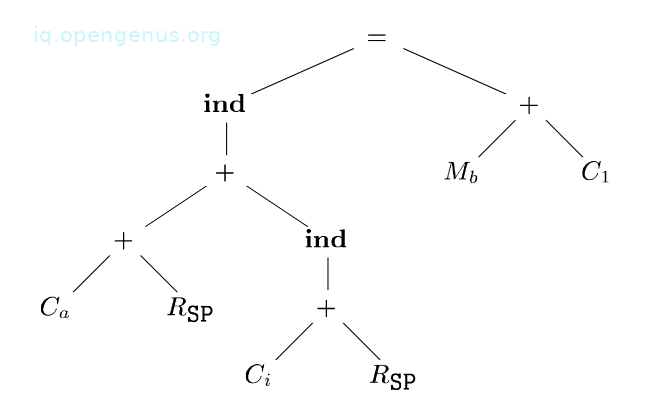
The array a is stored on the run-time stack and the variable b is a global in the memory location ${\mathrm{M}}_{\mathrm{b}}$.
The run-time addresses of locals a and i are given as constant offsets ${\mathrm{C}}_{\mathrm{a}}$ and ${\mathrm{C}}_{\mathrm{i}}$ from the register containing the the pointer to the beginning of the current activation record - SP.

The assignment to a[i] is an indirect assignment where the r-value of location a[i] is set to the r-value of b + 1.
We obtain the addresses of array a and variable i by adding the value of constants ${\mathrm{C}}_{\mathrm{a}}$ and ${\mathrm{C}}_{\mathrm{i}}$ to the contents of register SP.

To simplify the array-address calculation, we assume that all values are one-byte characters.
From the tree, the ind operator treats its argument as a memory address. It is the left child of an assignment operator and so it gives the location into which the r-value on the right side of the assignment operator is to be stored.

If an argument of a + or ind operator is a memory location or register, the contents of the memory location or register are taken as values.
The leaves of the tree are labeled with attributes, the subscript indicates the value of the attribute.

Now to generate target code, we apply a sequence of tree-rewriting rules to reduce the input tree to a single node. Each re-writing rule is of the form where replacement is a single node, template a tree, and action a code fragment, it's like in an SDT scheme.

A tree-translation scheme is a set of re-writing rules where each rule represents a translation of a portion of the tree by a given template.
A translation consists of possibly, an empty sequence of machine instructions emitted by an action associated with the template.

Leaves of the template are attributes with subscripts just like in the input tree.
At times, restrictions will apply to values of the subscripts in the templates, these are specified as semantic predicates that must be satisfied for a template to match.

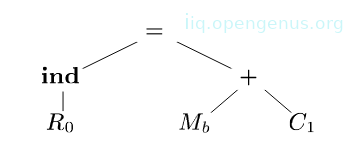
Let's look at a tree-rewriting rule for a register-to-register instruction:
[image 2]

The above rule states that, if the input tree has a matching subtree to the template, then we replace it by a single node labeled ${\mathrm{R}}_{\mathrm{i}}$ and give the instruction ADD ${\mathrm{R}}_{\mathrm{i}}$ ${\mathrm{R}}_{\mathrm{i}}$ ${\mathrm{R}}_{\mathrm{j}}$ as output.
Such a matching involves a subtree whose root is labeled by an operator + and whose left and right children are quantities in registers i and j.

Such a replacement is referred to as tiling a subtree which we discuss in the next section.

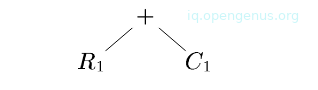
We have the following tree-rewriting rules for target-machine instructions.
[image 3]

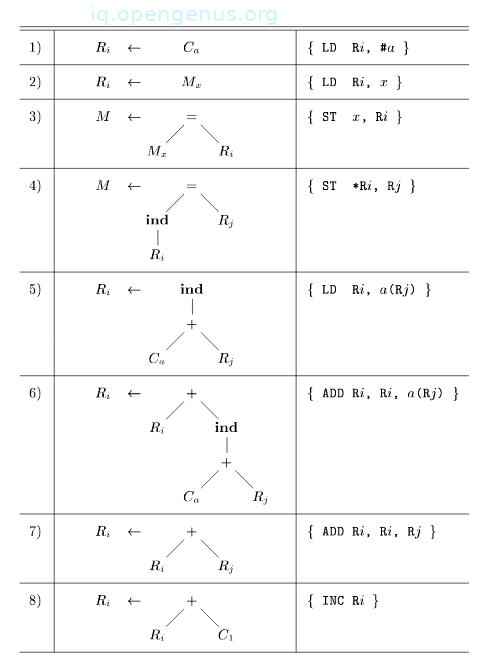
The first two instructions are load instructions.
The next two are store instructions.
The remaining rules are indexed loads and additions.

Tiling an input tree.

Steps in a tree translation scheme are as follows; We have a tree as input, we apply the tree-rewriting rules to its subtrees and if a matching exists we replace the subtree with the replacement node of the rule, and the action associated with the rule is done. However, if the action contains machine instructions, the instructions are emitted.
This is repeated until the tree is reduced to a single node or until no more templates match.

We would like to have a scheme that has a minimal cost in terms of the instruction sequence to be generated for each input tree.

An example:
We use the tree translation in [image 3] to generate code for the input tree in [image 1].
We apply the first rule to load constant ${\mathrm{C}}_{\mathrm{a}}$ in register R0.

1. 

The label of the leftmost leaf changes from ${\mathrm{C}}_{\mathrm{a}}$ to R0 and the instruction LD R0, #a is generated.
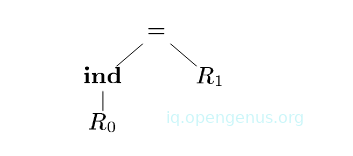
Now the seventh rule matches the leftmost subtree that has a root labeled +.

7. 

We rewrite this subtree as a single node labeled R0 and generate instruction ADD R0, R0, SP and we have the tree

We apply rule 5 and reduce the subtree and we have

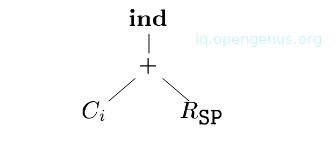
To a single node ${\mathrm{R}}_{\mathrm{1}}$, we apply rule 6 to reduce the larger subtree to a single node ${\mathrm{R}}_{\mathrm{0}}$ and generate the instruction ADD R0, R0 i(SP).

It is more efficient to use a single instruction to compute a larger subtree rather than a smaller, so we use rule 6 and we have

Rule 2 applies to leaf ${\mathrm{M}}_{\mathrm{b}}$ in the right subtree. It generates the instruction to load b into register R1.

We use rule 8 to match the subtree and generate the increment instruction INC R1

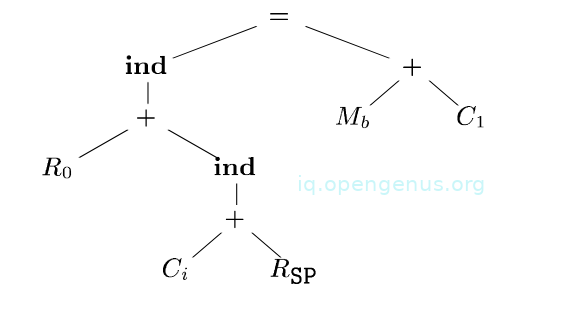
The input tree is now reduced to;

The remaining part of the tree is matched with rule 4 which reduced it into a single node and generates the instruction ST *RO, R1. We generate the code sequence below in the process of reducing the tree into a single node.

To implement a tree-reduction process we first address issues related to tree-pattern matching:
First, how is it performed? Mostly the tree-matching algorithm will affect the code generation process in terms of efficiency.

Secondly, what action do we take if there exists more than one template that matches? The efficiency of generated code depends on the order in which templates are matched since different match sequences lead to different target machine code sequences some more efficient than others.

When there are no templates that match, the process of code generation blocks. Keep in mind that we also need to prevent the possibility of a single node being rewritten indefinitely and generating an infinite sequence of register move instructions or an infinite sequence of loads and stores.

We prevent blocking by assuming that each operator in the intermediate code can be represented by one or more target-machine instructions.
We also assume that there are enough registers to compute each node of the tree.
Therefore no matter how the matching goes, the remaining tree will always be translated into target machine instructions.

Pattern matching.

In this section, we look at tree matching using an LR parser.
The input is a tree that is treated as a string by using prefix representation. For example, the prefix representation of the tree in [image 1] is:
= ind + + ${\mathrm{C}}_{\mathrm{a}}$ ${\mathrm{R}}_{\mathrm{SP}}$ ind + ${\mathrm{C}}_{\mathrm{i}}$${\mathrm{R}}_{\mathrm{SP}}$ + ${\mathrm{M}}_{\mathrm{b}}$${\mathrm{C}}_{\mathrm{1}}$

To convert it into an SDT scheme, we replace the tree-rewriting rules with the productions of a CFG whereby the right sides are prefix representations of the instruction templates.

An example:
Based on the tree-translation in [image 3] we have the following SDT scheme

The non-terminals of the grammar are R and M.
Terminal m represents memory location.
We can think of production M → m in rule 10 as a matching M with m before using one of the templates involving M.
Similarly, we introduce terminal sp for register SP and add the production R → sp.
The terminal c represents constants.

Using these terminals, the string for the input tree in [image 3] is
= ind + + ${\mathrm{c}}_{\mathrm{a}}$ sp ind + ${\mathrm{c}}_{\mathrm{i}}$ sp + ${\mathrm{m}}_{\mathrm{b}}$ ${\mathrm{c}}_{\mathrm{1}}$

From the translation scheme, we build an LR parser using an LR parser construction technique.
The benefits of using LR parsing in code generation involves the ease of understanding an efficient parsing method and easy retargeting of the resulting code generator.

However, challenges of this exist, for example, a left-to-right evaluation is fixed by the parsing method, secondly, some machines with a large number of addressing modes result in a large machine-description grammar and parser.

Generalized tree matching.

We have seen the LR-parsing approach and learned that it is based on prefix representations that favor the left operand of a binary operator.
This pattern-matching could miss nuances of the target instruction set due to the right operands.

Therefore instead of prefix representation, we use postfix representation although this also would favor the right operand.

For hand-written code generators, we use tree templates as a guide to writing an ad-hoc matcher.
For this, we need an efficient top-down algorithm that is developed by extending string-pattern-matching techniques.
The general idea is to represent each term as a set of strings whereby a string corresponds to a path from the root to the leaf in the template.
In this case, we treat all operands equally by also including the position number of a child from left to right in the strings.

An example:
To build a set of strings for an instruction set, we drop the subscripts since pattern matching is based on only attributes.

Given the following templates:

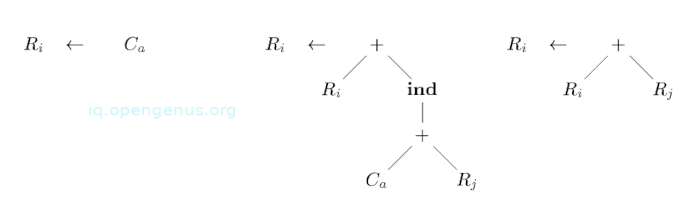
We have the following have the following set of strings from root to leaf:

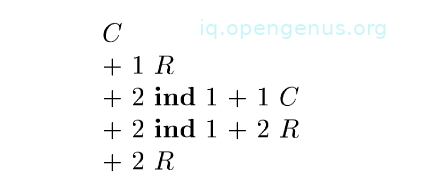
C represents a template with C at the root.
+1R represents the + and its left operand R in the two templates that have + at the root.

Using the set of strings, we can construct a tree-pattern matcher using techniques for matching multiple strings in parallel efficiently.

In practice, tree-rewriting is implemented by running a tree-pattern matcher during a depth-first traversal of the input tree and performing reductions as the nodes are visited for the last time.
We take instruction costs into account by associating each rule with the cost of the sequence of machine instructions generated if the rule is applied.

In another article, we have discussed how dynamic programming is combined with tree-pattern matching to select optimal sequences of matches using cost information associated with each rule.
The dynamic programming technique frees a code-generator designer from having to resolve conflicting matches or decide on an ordering for evaluation.

Summary.

Code generation is the final phase in a compiler where IR is mapped into the target program.

The process of selecting target-language instructions for each IR statement is referred to as pattern matching.

We have seen how instruction selection can be done by tree-rewriting whereby tree patterns that correspond to machine instructions are used to tile a syntax tree.
In this process, we associate costs with tree-rewriting rules and apply dynamic programming in order to obtain an optimal tiling for a wide range of machines and expressions.

References.

1. dynamic programming for code generation.