
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 12 minutes | Coding time: 6 minutes
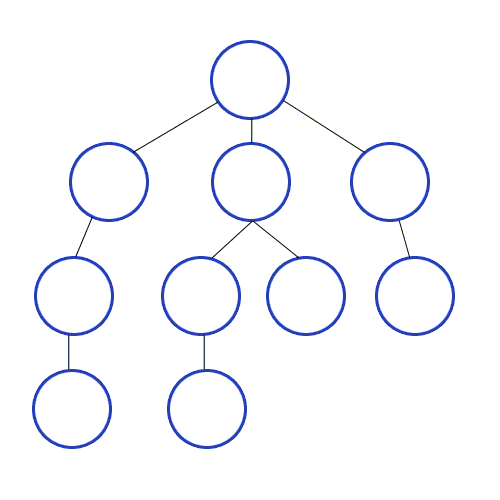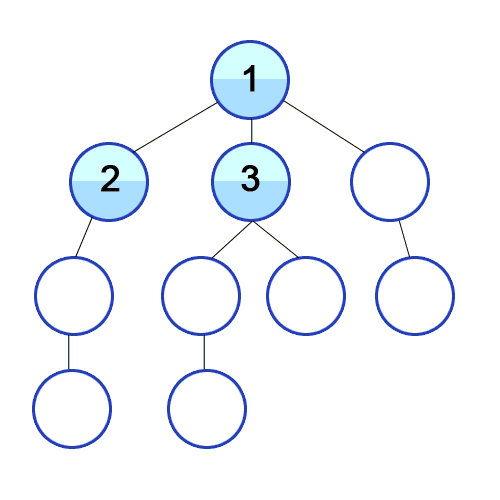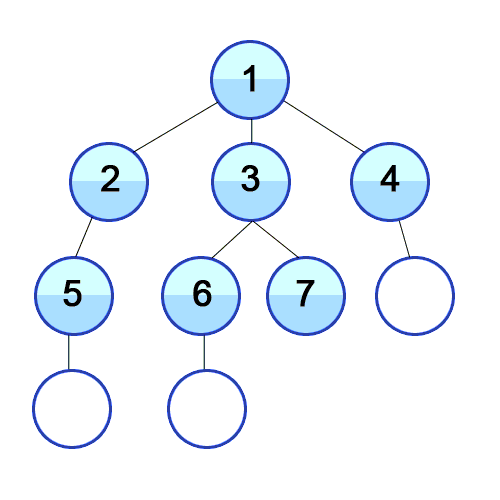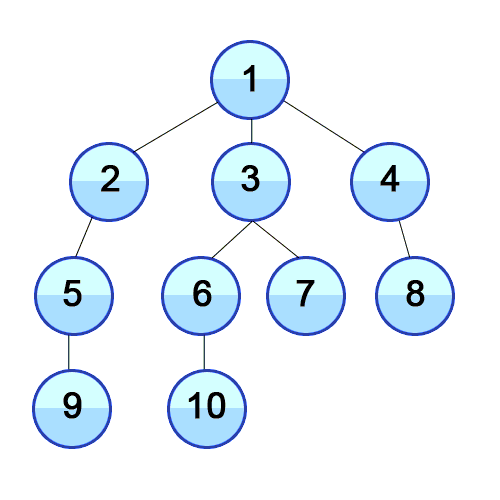
Breadth-first search (BFS) algorithm is an algorithm for traversing or searching tree or graph data structures. One starts at the root (selecting some arbitrary node as the root in the case of a graph) and explores along adjacent nodes and proceeds recursively.
Complexity
- Worst case time complexity:
Θ(V+E) - Average case time complexity:
Θ(V+E) - Best case time complexity:
Θ(V+E) - Space complexity:
Θ(V)
Pseudocode
BFS(v):
for each vertex i
do d[i] = inf
d[v] = 0
queue q
q.push(v)
while q is not empty
u = q.front()
q.pop()
for each w in adj[u]
if d[w] == inf
then d[w] = d[u] + 1, q.push(w)
where distance of vertex u from v is d[u].
Implementations
Implementation of Breadth First Search algorithm in 6 languages that includes C, C++, Java, Ruby, Python and Swift.
- C
- C++
- Java
- Ruby
- Python
- Swift
C
#include <stdio.h>
#include <stdlib.h>
struct node
{
int data;
struct node* next;
};
int del(struct node** head,int* element);
int add(struct node** head,int element);
//main program
int main()
{
//input no of nodes: Num
int Num;
printf("Enter number of nodes\n");
scanf("%d",&Num);
//create adjacency matrix
int adj[Num][Num];
//input adjacency matrix
printf("Enter adjacency matrix\n");
for(int i=0;i<Num;i++)
{
for(int j=0;j<Num;j++)
{
scanf("%d",&adj[i][j]);
}
}
//BFS traversing
//create a queue
struct node *Queue=NULL;
//create status array and set it to ready state
enum{ready,waiting,processed};
int status[Num];
for(int i=0;i<Num;i++)
{
status[i]=ready;
}
//add first node to queue
add(&Queue,0);
status[0]=waiting;
int node=NULL;
printf("BFS traversing\n");
while(Queue!=NULL)
{
//get a node from queue, display it and change status to processed
del(&Queue,&node);
printf("%d ",node);
status[node]=processed;
//add it's neighbours with status ready to queue
for(int i=0;i<Num;i++)
{
if(adj[node][i]==1 && status[i]==ready)
{
add(&Queue,i);
status[i]=waiting;
}
}
}
printf("\n");
}
//queue functions
int del(struct node** head,int* element)
{
if(*head==NULL)
return 1;
*element=(*head)->data;
struct node* temp;
temp=*head;
*head=(*head)->next;
free(temp);
return 0;
}
int add(struct node** head,int element)
{
if((*head)==NULL)
{
*head=(struct node*)malloc(sizeof(struct node));
(*head)->next=NULL;
(*head)->data=element;
return 0;
}
struct node* temp=*head;
while(temp->next!=NULL)
{
temp=temp->next;
}
temp->next=(struct node*)malloc(sizeof(struct node));
if(temp->next==NULL)
return 1;
temp=temp->next;
temp->data=element;
temp->next=NULL;
return 0;
}
C++
#include <iostream>
#include <map>
#include <set>
#include <queue>
/* Part of Cosmos by OpenGenus Foundation */
void bfs(int start, // the node that we are currently at
std::map<int, std::set<int>>& adjList, // the adjacency list for each node
std::map<int, bool>& visited, // the 'visited' state for each node
std::map<int, int>& distance // the distance from the `start` node
) {
// First, clear the distance map, so that only nodes that we can actually reach from the `start` appear in it at the end
distance.clear();
// This queue wil hold pairs of numbers of the form (nodeNumber, distance)
std::queue<std::pair<int, int>> Q;
// Add the first node with distance 0 to the queue and mark it as visited
Q.push(std::make_pair(start, 0));
visited[start] = true;
// Repeat the algorithm until there are no more ndoes left to process
while (!Q.empty()) {
// Take the node from the front of the queue and pop it off the queue
auto entry = Q.front(); Q.pop();
int node = entry.first;
int dist = entry.second;
// Put the distance to this node into the distance map (this is the minimal distance to this node)
distance[node] = dist;
// Iterate over the neighbours of the current node
for (auto neighbour : adjList[node]) {
if (!visited[neighbour]) {
// Mark the neighbour node as visited
visited[neighbour] = true;
Q.push(std::make_pair(neighbour, dist + 1));
}
}
}
}
void addEdge(int a, int b, std::map<int, std::set<int>>& adjList) {
adjList[a].insert(b);
adjList[b].insert(a);
}
int main() {
/*
Do a breadth-first search in this graph:
1--2--4--7
| / \ |
|/ \ |
3 5--6
8--9
*/
std::map<int, std::set<int>> adjList;
std::map<int, bool> visited;
std::map<int, int> dist;
addEdge(1, 2, adjList);
addEdge(1, 3, adjList);
addEdge(2, 3, adjList);
addEdge(2, 4, adjList);
addEdge(2, 5, adjList);
addEdge(4, 7, adjList);
addEdge(5, 6, adjList);
addEdge(6, 7, adjList);
addEdge(8, 9, adjList);
// Set all nodes as unvisited at first
for (int i = 1; i <= 8; i++) visited[i] = false;
// Perform a bfs from the node `1`
bfs(1, adjList, visited, dist);
// Print the distance to all visited nodes
for (auto entry : dist) {
std::cout << "Distance from 1 to " << entry.first << " is " << entry.second << std::endl;
}
return 0;
}
Java
// Java program to print BFS traversal from a given source vertex.
import java.io.*;
import java.util.*;
// Part of Cosmos by OpenGenus Foundation
// This class represents a directed Graph using adjacency list representation
class Bfs
{
private int V; // No. of vertices
private LinkedList<Integer> adj[]; //Adjacency Lists
// Constructor of the class
Bfs(int v) {
V = v;
adj = new LinkedList[v];
for (int i = 0; i < v; ++i) {
adj[i] = new LinkedList();
}
}
// Function to add an edge into the Graph
void addEdge(int v,int w) {
adj[v].add(w);
}
// prints BFS traversal from a given source s
void BFS(int s) {
// Mark all the vertices as not visited(By default
// set as false)
boolean visited[] = new boolean[V];
// Create a queue for BFS
LinkedList<Integer> queue = new LinkedList<Integer>();
// Mark the current node as visited and enqueue it
visited[s]=true;
queue.add(s);
while (queue.size() != 0) {
// Dequeue a vertex from queue and print it
s = queue.poll();
System.out.print( s + " ");
// Get all adjacent vertices of the dequeued vertex s
// If a adjacent has not been visited, then mark it visited and enqueue it
Iterator<Integer> i = adj[s].listIterator();
while( i.hasNext()) {
int n = i.next();
if ( !visited[n] ) {
visited[n] = true;
queue.add(n);
}
}
}
}
// Driver method to
public static void main(String args[]) {
Bfs g = new Bfs(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.addEdge(3, 3);
System.out.println("Following is Breadth First Traversal "+"(starting from vertex 2)");
g.BFS(2);
System.out.println();
}
}
Ruby
# This class represents a node in a graph.
# It has a NAME and an ID and each node knows which nodes it is connected to.
class GraphNode
require 'set'
@@id = 0
attr_reader :name, :id, :connections
def initialize(name)
@name = name
@id = (@@id += 1)
@connections = Set.new
end
def connect(node)
return false unless node.is_a? GraphNode
@connections << node
end
def equal?(other)
return false unless other.is_a? GraphNode
@name == other.name && @id == other.id
end
def to_s
"<GraphNode:#{name}>"
end
def to_str
to_s
end
end
# A simple function as a default function performed for each node in bfs()
def goalNode?(node)
node.name == 'Goal'
end
# Given a start node and a function or code block this performs a bread first search and will exit upon function or code block returning true, or returns :goal_node_not_found when it has visited the whole graph.
#
# visited is a set containing all nodes that has been checked.
# frontier is a queue were new nodes are appended, making this a breadth first search.
def bfs(start, goal = :goalNode?)
require 'set'
visited = Set.new
frontier = []
frontier << start
until frontier.empty?
current = frontier.shift
next if visited.include? current
visited << current
found = false
found = if block_given?
yield(current)
else
send(goal, current)
end
if !found
current.connections.each do |node|
frontier << node
end
else
return current
end
end
:goal_node_not_found
end
# A small test that will use bfs() for root node First, then for the Second node.
# The bfs accepts a code block, and here we just print each visited node and will never find the goal-node.
#
# The tests output:
# Testing from root node 'First'
# <GraphNode:First>
# <GraphNode:Second>
# <GraphNode:Third>
# <GraphNode:Fourth>
# <GraphNode:Fifth>
# <GraphNode:Goal>
# <GraphNode:Sixth>
# goal_node_not_found
# Testing from second node 'Second'
# <GraphNode:Second>
# <GraphNode:First>
# <GraphNode:Fourth>
# <GraphNode:Fifth>
# <GraphNode:Third>
# <GraphNode:Goal>
# <GraphNode:Sixth>
# goal_node_not_found
def test
puts 'Building Graph for tests...'
# Simple graph
#
# First
# / \
# second third
# / | | \
# fourth fifth goal sixth
#
# Construct graph
first = GraphNode.new 'First'
second = GraphNode.new 'Second'
third = GraphNode.new 'Third'
fourth = GraphNode.new 'Fourth'
fifth = GraphNode.new 'Fifth'
sixth = GraphNode.new 'Sixth'
goal = GraphNode.new 'Goal'
first.connect second
first.connect third
second.connect first
second.connect fourth
second.connect fifth
third.connect first
third.connect goal
third.connect sixth
fourth.connect second
fifth.connect second
goal.connect third
sixth.connect third
# Perform tests
puts "Testing from root node 'First'"
puts(bfs(first) { |node| puts ' ' + node })
puts "Testing from second node 'Second'"
puts(bfs(second) { |node| puts ' ' + node })
end
test if $PROGRAM_NAME == __FILE__
Python
""" Part of Cosmos by OpenGenus Foundation"""
import collections
"""
Wrapper function for the print function.
Used as the default visitFunc for bfs
"""
def visitPrint(i):
print(i)
"""
A class representing a undirected graph of nodes.
An edge can be added between two nodes by calling addEdge
*This class assumes all edge weights are equal
"""
class Graph:
def __init__(self):
self.adjList = collections.defaultdict(set)
def addEdge(self, node1, node2):
self.adjList[node1].add(node2)
self.adjList[node2].add(node1)
"""
Given a 'start' node and a 'graph', call visitFunc
sequentially on the current node, and then its children
and so forth.
When visiting each node, mark it as visited by adding it to the hashmap.
Then queue up all of its children to be visited next.
"""
def bfs(start, graph, visitFunc=visitPrint):
visited = collections.defaultdict(bool)
queue = collections.deque()
queue.append(start)
while(len(queue) > 0):
current = queue.popleft()
if (not visited[current]):
visited[current] = True
visitFunc(current)
for neighbor in graph.adjList[current]:
queue.append(neighbor)
# Testing the breadth first search implementation
if __name__ == "__main__":
# Testing on this tree
# 1
# / \
# / \
# 2 3
# / \ / \
# 4 5 6 7
g = Graph()
g.addEdge(1, 2)
g.addEdge(1, 3)
g.addEdge(2, 4)
g.addEdge(2, 5)
g.addEdge(3, 6)
g.addEdge(3, 7)
print("Test 1:")
bfs(1, g)
print("\nTest2:")
bfs(2, g)
"""Output:
Test 1:
1
2
3
4
5
6
7
Test2:
2
1
4
5
3
6
7
"""
Swift
func breadthFirstSearch(_ graph: Graph, source: Node) -> [String] {
var queue = Queue<Node>()
queue.enqueue(source)
var nodesExplored = [source.label]
source.visited = true
while let current = queue.dequeue() {
for edge in current.neighbors {
let neighborNode = edge.neighbor
if !neighborNode.visited {
queue.enqueue(neighborNode)
neighborNode.visited = true
nodesExplored.append(neighborNode.label)
}
}
}
return nodesExplored
}
Applications
- Shortest Path and Minimum Spanning Tree for unweighted graph
- Find neighboring nodes like in Peer to Peer Networks, Crawlers in search engine, potential friends in social networks, GPS navigation system, broadcasting in network and many others.
- In Garbage Collection: Breadth First Search is used in copying garbage collection using Cheney’s algorithm.
- Cycle detection in undirected graph
- Ford–Fulkerson algorithm
- To test if a graph is Bipartite
- Path Finding
