Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 15 minutes | Coding time: 9 minutes
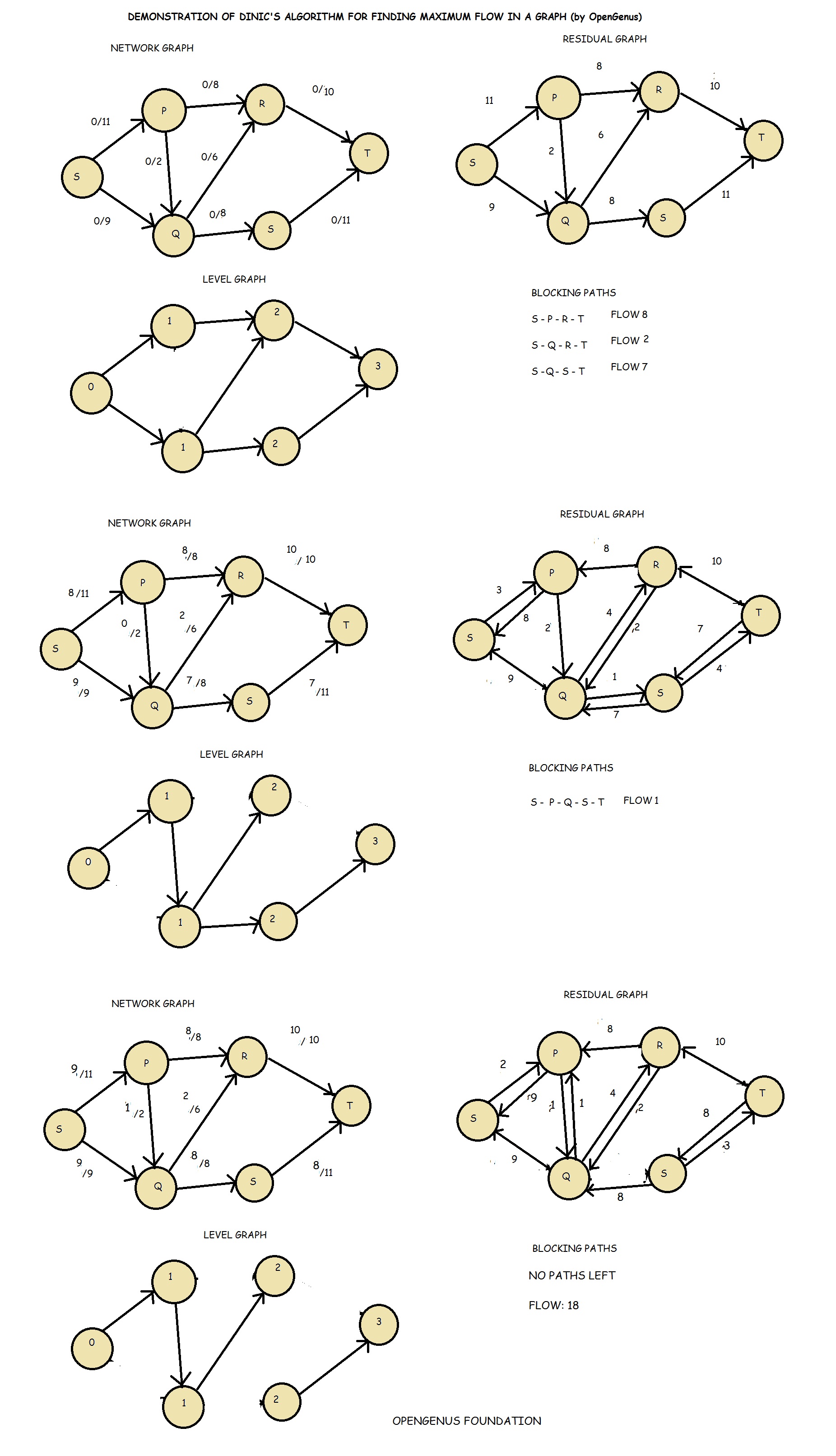
Dinic's algorithm or Dinitz's algorithm is a strongly polynomial algorithm for computing the maximum flow in a flow network. The basic principle is that a Maximum flow = minimum cut and Breadth First Search is used as a sub-routine.
The credit of Dinic's algorithm goes to computer scientist Yefim (Chaim) A. Dinitz.
Pseudocode
1.set f(e) = 0 for each e in E
2.Construct G_L from G_f of G. if dist(t) == inf, then stop and output f
3.Find a blocking flow fp in G_L
4.Augment flow f by fp and go back to step 2.
Level graph is one where value of each node is its shortest distance from source.
Blocking flow includes finding the new path from the bottleneck node.
An augmenting path is a simple path from source to sink which do not include any cycles and that pass only through positive weighted edges. A residual network graph indicates how much more flow is allowed in each edge in the network graph. If there are no augmenting paths possible from to , then the flow is maximum.
Follow the following illustrative example of Dinic's algorithm:
Complexity
- Worst case time complexity:
Θ(E * V * V) - Average case time complexity:
Θ(E * V * V) - Best case time complexity:
Θ(E * V * V) - Space complexity:
Θ(E + V)
Implementations
- C++
C++
#include <vector>
#include <queue>
#include <cstring>
#include <iostream>
// Part of Cosmos by OpenGenus Foundation
struct edge
{
int to;
int cap;
int rev;
};
class dinic
{
private:
int INF;
std::vector<edge> G[100000];
int level[100000];
int iter[100000];
public:
dinic();
void add_edge(int from, int to, int cap);
void bfs(int s);
int dfs(int v, int t, int f);
int maximum_flow(int s, int t);
};
dinic::dinic()
{
INF = 0x7fffffff;
std::fill(level, level + 100000, 0);
std::fill(iter, iter + 100000, 0);
}
void dinic::add_edge(int from, int to, int cap)
{
G[from].push_back((edge){to, cap, (int)G[to].size()});
G[to].push_back((edge){from, 0, (int)G[from].size() - 1});
}
void dinic::bfs(int s)
{
std::memset(level, -1, sizeof(level));
std::queue<int> que;
level[s] = 0;
que.push(s);
while (!que.empty())
{
int v = que.front();
que.pop();
for (int i = 0; i < (int)G[v].size(); i++)
{
edge &e = G[v][i];
if (e.cap > 0 && level[e.to] < 0)
{
level[e.to] = level[v] + 1;
que.push(e.to);
}
}
}
}
int dinic::dfs(int v, int t, int f)
{
if (v == t)
return f;
for (int &i = iter[v]; i < (int)G[v].size(); i++)
{
edge &e = G[v][i];
if (e.cap > 0 && level[v] < level[e.to])
{
int d = dfs(e.to, t, std::min(f, e.cap));
if (d > 0)
{
e.cap -= d;
G[e.to][e.rev].cap += d;
return d;
}
}
}
return 0;
}
int dinic::maximum_flow(int s, int t)
{
int flow = 0;
for (;;)
{
bfs(s);
if (level[t] < 0)
return flow;
std::memset(iter, 0, sizeof(iter));
int f;
while ((f = dfs(s, t, INF)) > 0)
flow += f;
}
}
Applications
- maximizing the transportation with given traffic limits
- maximizing packet flow in computer networks.