Maximum sum leaf to root path

In this article, I will be discussing about Maximum sum leaf to root path in Binary tree along with time and space complexity.

Contents:

• Introduction
• Problem Approach
• Implementation
• Time and Space Complexity Analysis

Introduction:

Suppose we are Given a Binary Tree, and we have to find the maximum sum path from a leaf to root. For example, in the following tree, there are three leaf to root paths 8->-2->10, 9->-2->10 and 3->10. The sums of these three paths are 16, 17 and 13 respectively.

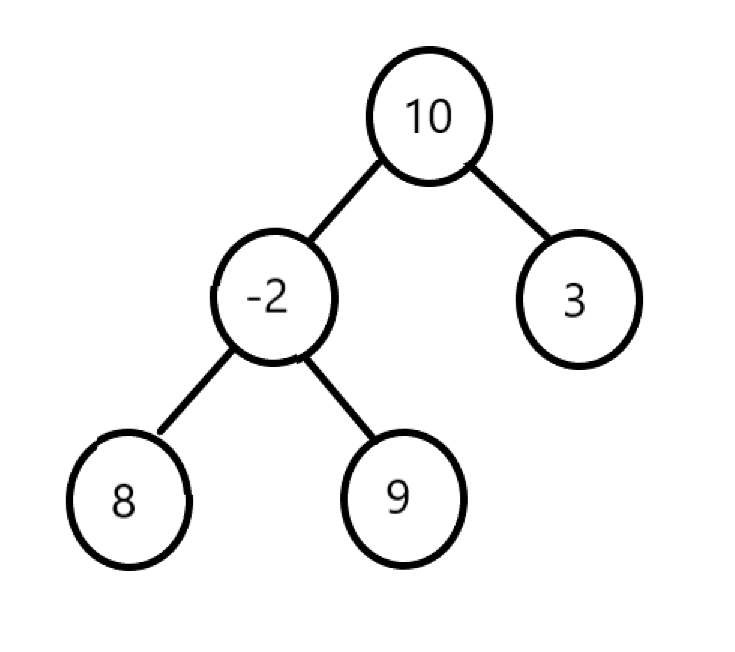
The maximum of them is 17 and the path for maximum is 9->-2->10.

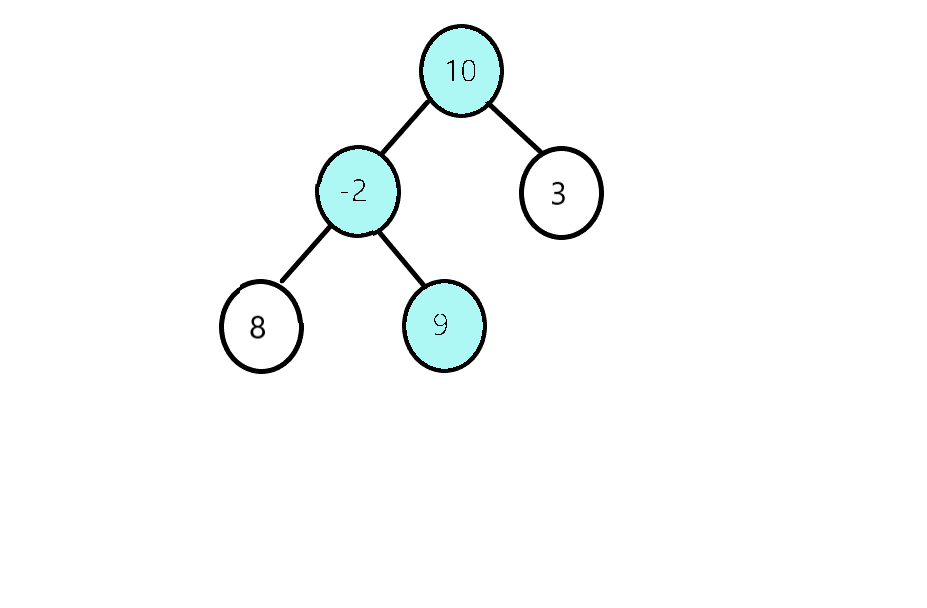
Problem Approach:

The basic idea to solve this problem is to add the value of each node in a particular path till we reach the leaf node. After reaching the leaf node we will update the maximum path sum.

1. We will create a function sum which will traverse every root to leaf path recursively and update the maximum sm value;
2. In the sum function first we will add the value of the root node and then recursively call for the left sub-tree and then for the right subtree respectively.
3. once we reach to the leaf node, then we update our maximum-path-sum by comparing from our previous-path-sum.
4. After executing the above steps, we will get our maximum root to leaf path sum.

Implementation:

class Node {
    int data;
    Node left, right;
  
    Node(int item)
    {
        data = item;
        left = right = null;
    }
}
class Solution
{
    public int res =Integer.MIN_VALUE;
    public int maxPathSum(Node root)
    {
        //code here
        sum(root,0);
    
        return res;
        
    }
    public void sum(Node root,int sum){
        if(root==null){
            return;
        }
        sum +=root.data;
        if(root.left==null && root.right==null){
            res = Math.max(sum,res);
            return;
        }
        sum(root.left,sum);
        sum(root.right,sum);
        return;
        
    }
}

Time and Space Complexity Analysis:

The time complexity of the above solution will be O(N),where N is total number of nodes in the binary tree. As the above appraoch traveses each node two times or traveses the tree tree two times, so the overall complexity of the above solution will be O(N).

The space complexity of the above solution will be O(H), where H is the height of the tree. As we know the right sub-tree call will not execute till the left sub-tree call has completed its execution, so at a time there will be atmost H function calls in the call stack.