
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 15 minutes | Coding time: 9 minutes
Ford–Fulkerson algorithm is a greedy algorithm that computes the maximum flow in a flow network. The main idea is to find valid flow paths until there is none left, and add them up. It uses Depth First Search as a sub-routine.
Pseudocode
* Set flow_total = 0
* Repeat until there is no path from s to t:
* Run Depth First Search from source vertex s to find a flow path to end vertex t
* Let f be the minimum capacity value on the path
* Add f to flow_total
* For each edge u → v on the path:
* Decrease capacity of the edge c(u → v) by f
* Increase capacity of the edge c(v → u) by f
Before moving forward, think about the following questions:
-
What is the worst case scenario for Ford Fulkerson algorithm?
-
Will Ford Fulkerson algorithm terminate for all graphs?
Worst case scenario:
Flow increments by 1 in each step for a graph such as:
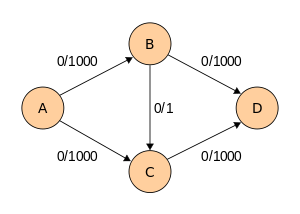
It takes 2000 steps to find the maximum flow in the above graph. If we used Breadth First Search instead of Depth First Search in Ford Fulkerson algorithm, it will take 2 steps.
Non-terminating example:
Ford Fulkerson algorithm will not terminate for the following graph:
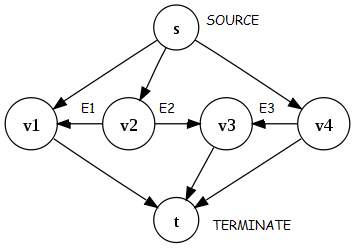
How do we know if this gives a maximum flow?
Proof overview:
We will use proof by contradiction.
Suppose Ford–Fulkerson algorithm will not give the maximum flow.
Take a maximum flow f and “subtract” our flow f. It is a valid flow of positive total flow. By the flow decomposition, it can be decomposed into flow paths and circulations. These flow paths must have been found by Ford-Fulkerson.
This leds to a contradiction. Hence, Ford–Fulkerson algorithm will give the maximum flow.
Complexity
- Worst case time complexity:
Θ(max_flow * E) - Average case time complexity:
Θ(max_flow * E) - Best case time complexity:
Θ(max_flow * E) - Space complexity:
Θ(E + V)
Implementations
- C++
- Java
- Python
C++
/* Part of Cosmos by OpenGenus Foundation */
#include <iostream>
#include <string.h>
using namespace std;
#define N 7
#define INF 9999999
// flow network
int Flow[N][N];
// visited array
bool visited[N];
// original flow network graph shown in the above example
//0 1 2 3 4 5 6
int graph[N][N] = {
{ 0, 5, 4, 0, 0, 0, 0 }, //0
{ 0, 0, 0, 0, 0, 0, 4 }, //1
{ 0, 0, 0, 3, 0, 0, 6 }, //2
{ 0, 0, 0, 0, 5, 0, 0 }, //3
{ 0, 0, 0, 0, 0, 0, 8 }, //4
{ 6, 0, 0, 2, 0, 0, 0 }, //5
{ 0, 0, 0, 0, 0, 0, 0 }, //6
};
int dfs(int s, int t, int minimum) {
visited[s] = true;
// if source and sink is same
if (s == t)
return minimum;
for (int i = 0; i < N; i++) {
int flow_capacity = graph[s][i] - Flow[s][i];
if (!visited[i] && flow_capacity > 0) {
// find min capacity in dfs path
if (int sent = dfs (i, t, min (minimum, flow_capacity))) {
// adjust the capacity
Flow[s][i] += sent;
Flow[i][s] -= sent;
return sent;
}
}
}
return false;
}
int main() {
// initialize initial flow capacity 0
memset(Flow, 0, sizeof(Flow));
// initialize visited array false initially
memset(visited, 0, sizeof(visited));
int s = 5;
int t = 6;
int max_flow = 0;
// while ther is augmenting path , from s and t
// with positive flow capacity
while (int sent = dfs(s, t, INF)) {
max_flow += sent;
// reset visited array , for searching next path
memset(visited, 0, sizeof(visited));
}
cout << "The max flow from node 5 to sink node 6 is " << max_flow;
cout << endl;
}
Java
// Part of Cosmos by OpenGenus Foundation
import java.util.LinkedList;
import java.lang.Exception;
class FordFulkersonUsingBfs {
static final int V = 6;
boolean bfs(int rGraph[][], int s, int t, int parent[]) {
/*
* Create a visited array and mark all vertices as not
* visited
*/
boolean visited[] = new boolean[V];
for(int i=0; i<V; ++i)
visited[i]=false;
/*
* Create a queue, enqueue source vertex and mark
* source vertex as visited
*/
LinkedList<Integer> queue = new LinkedList<Integer>();
queue.add(s);
visited[s] = true;
parent[s]=-1;
// Standard BFS Loop
while (queue.size()!=0)
{
int u = queue.poll();
for (int v=0; v<V; v++)
{
if (visited[v]==false && rGraph[u][v] > 0)
{
queue.add(v);
parent[v] = u;
visited[v] = true;
}
}
}
/*
* If we reached sink in BFS starting from source, then
* return true, else false
*/
return (visited[t] == true);
}
// Returns tne maximum flow from s to t in the given graph
int fordFulkerson(int graph[][], int s, int t)
{
int u, v;
/*
* Create a residual graph and fill the residual graph
* with given capacities in the original graph as
* residual capacities in residual graph
*/
/*
* Residual graph where rGraph[i][j] indicates
* residual capacity of edge from i to j (if there
* is an edge. If rGraph[i][j] is 0, then there is
* not)
*/
int rGraph[][] = new int[V][V];
for (u = 0; u < V; u++)
for (v = 0; v < V; v++)
rGraph[u][v] = graph[u][v];
// This array is filled by BFS and to store path
int parent[] = new int[V];
int max_flow = 0; // There is no flow initially
/*
* Augment the flow while tere is path from source
* to sink
*/
while (bfs(rGraph, s, t, parent))
{
/*
*Find minimum residual capacity of the edhes
* along the path filled by BFS. Or we can say
* find the maximum flow through the path found.
*/
int pathFlow = Integer.MAX_VALUE;
for (v=t; v!=s; v=parent[v])
{
u = parent[v];
pathFlow = Math.min(pathFlow, rGraph[u][v]);
}
/*
* update residual capacities of the edges and
* reverse edges along the path
*/
for (v=t; v != s; v=parent[v])
{
u = parent[v];
rGraph[u][v] -= pathFlow;
rGraph[v][u] += pathFlow;
}
// Add path flow to overall flow
max_flow += pathFlow;
}
// Return the overall flow
return max_flow;
}
// Driver program to test above functions
public static void main (String[] args) throws java.lang.Exception {
// Example graph in adjancancy matrix
int graph[][] =new int[][] { {0, 16, 13, 0, 0, 0},
{0, 0, 10, 12, 0, 0},
{0, 4, 0, 0, 14, 0},
{0, 0, 9, 0, 0, 20},
{0, 0, 0, 7, 0, 4},
{0, 0, 0, 0, 0, 0}
};
FordFulkersonUsingBfs m = new FordFulkersonUsingBfs();
System.out.println("The maximum possible flow is " +
m.fordFulkerson(graph, 0, 5));
}
}
Python
'''
Part of Cosmos by OpenGenus Foundation
'''
from collections import defaultdict
#This class represents a directed graph using adjacency matrix representation
class Graph:
def __init__(self,graph):
self.graph = graph # residual graph
self. ROW = len(graph)
#self.COL = len(gr[0])
'''Returns true if there is a path from source 's' to sink 't' in
residual graph. Also fills parent[] to store the path '''
def BFS(self,s, t, parent):
# Mark all the vertices as not visited
visited =[False]*(self.ROW)
# Create a queue for BFS
queue=[]
# Mark the source node as visited and enqueue it
queue.append(s)
visited[s] = True
# Standard BFS Loop
while queue:
#Dequeue a vertex from queue and print it
u = queue.pop(0)
# Get all adjacent vertices of the dequeued vertex u
# If a adjacent has not been visited, then mark it
# visited and enqueue it
for ind, val in enumerate(self.graph[u]):
if visited[ind] == False and val > 0 :
queue.append(ind)
visited[ind] = True
parent[ind] = u
# If we reached sink in BFS starting from source, then return
# true, else false
return True if visited[t] else False
# Returns tne maximum flow from s to t in the given graph
def FordFulkerson(self, source, sink):
# This array is filled by BFS and to store path
parent = [-1]*(self.ROW)
max_flow = 0 # There is no flow initially
# Augment the flow while there is path from source to sink
while self.BFS(source, sink, parent) :
# Find minimum residual capacity of the edges along the
# path filled by BFS. Or we can say find the maximum flow
# through the path found.
path_flow = float("Inf")
s = sink
while(s != source):
path_flow = min (path_flow, self.graph[parent[s]][s])
s = parent[s]
# Add path flow to overall flow
max_flow += path_flow
# update residual capacities of the edges and reverse edges
# along the path
v = sink
while(v != source):
u = parent[v]
self.graph[u][v] -= path_flow
self.graph[v][u] += path_flow
v = parent[v]
return max_flow
# Create a graph given in the above diagram
print("Enter the number of vertices: ", end="")
m = int(input())
matrix = []
for i in range(0,m):
matrix.append([])
for j in range(0,m):
print("Enter the edge value from " + str(i) + " to " + str(j) +": ", end="")
temp = int(input())
matrix[i].append(temp)
print("\nthe matrix is,\n")
for i in range(0,m):
for j in range(0,m):
print(matrix[i][j]," ",end="")
print("\n")
print("Enter the source: ", end="")
source = int(input())
print("Enter the sink: ", end="")
sink = int(input())
print ("The maximum possible flow is %d " % g.FordFulkerson(source, sink))
Applications
- maximizing the transportation with given traffic limits
- maximizing packet flow in computer networks.
