
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we have explored Depth Limited Search algorithm which is a restricted version of Depth First Search (DFS).
Table of contents:
- Introduction to Depth Limited Search
- Depth Limited Search Algorithm
- Step by Step Example
- Implementation
- Advantages of Depth Limited Search
- Disadvantages of Depth Limited Search
- Measures of Performance
- Comparison of DLS with BFS and DFS
- Conclusion
Introduction to Depth Limited Search
Depth limited search is an uninformed search algorithm which is similar to Depth First Search(DFS). It can be considered equivalent to DFS with a predetermined depth limit 'l'. Nodes at depth l are considered to be nodes without any successors.
Depth limited search may be thought of as a solution to DFS's infinite path problem; in the Depth limited search algorithm, DFS is run for a finite depth 'l', where 'l' is the depth limit.
Before moving on to the next path, a Depth First Search starts at the root node and follows each branch to its deepest node. The problem with DFS is that this could lead to an infinite loop. By incorporating a specified limit termed as the depth limit, the Depth Limited Search Algorithm eliminates the issue of the DFS algorithm's infinite path problem; In a graph, the depth limit is the point beyond which no nodes are explored.
Depth Limited Search Algorithm
We are given a graph G and a depth limit 'l'. Depth Limited Search is carried out in the following way:
- Set STATUS=1(ready) for each of the given nodes in graph G.
- Push the Source node or the Starting node onto the stack and set its STATUS=2(waiting).
- Repeat steps 4 to 5 until the stack is empty or the goal node has been reached.
- Pop the top node T of the stack and set its STATUS=3(visited).
- Push all the neighbours of node T onto the stack in the ready state (STATUS=1) and with a depth less than or equal to depth limit 'l' and set their STATUS=2(waiting).
(END OF LOOP) - END
When one of the following instances are satisfied, a Depth Limited Search can be terminated.
- When we get to the target node.
- Once all of the nodes within the specified depth limit have been visited.
Step by Step Example
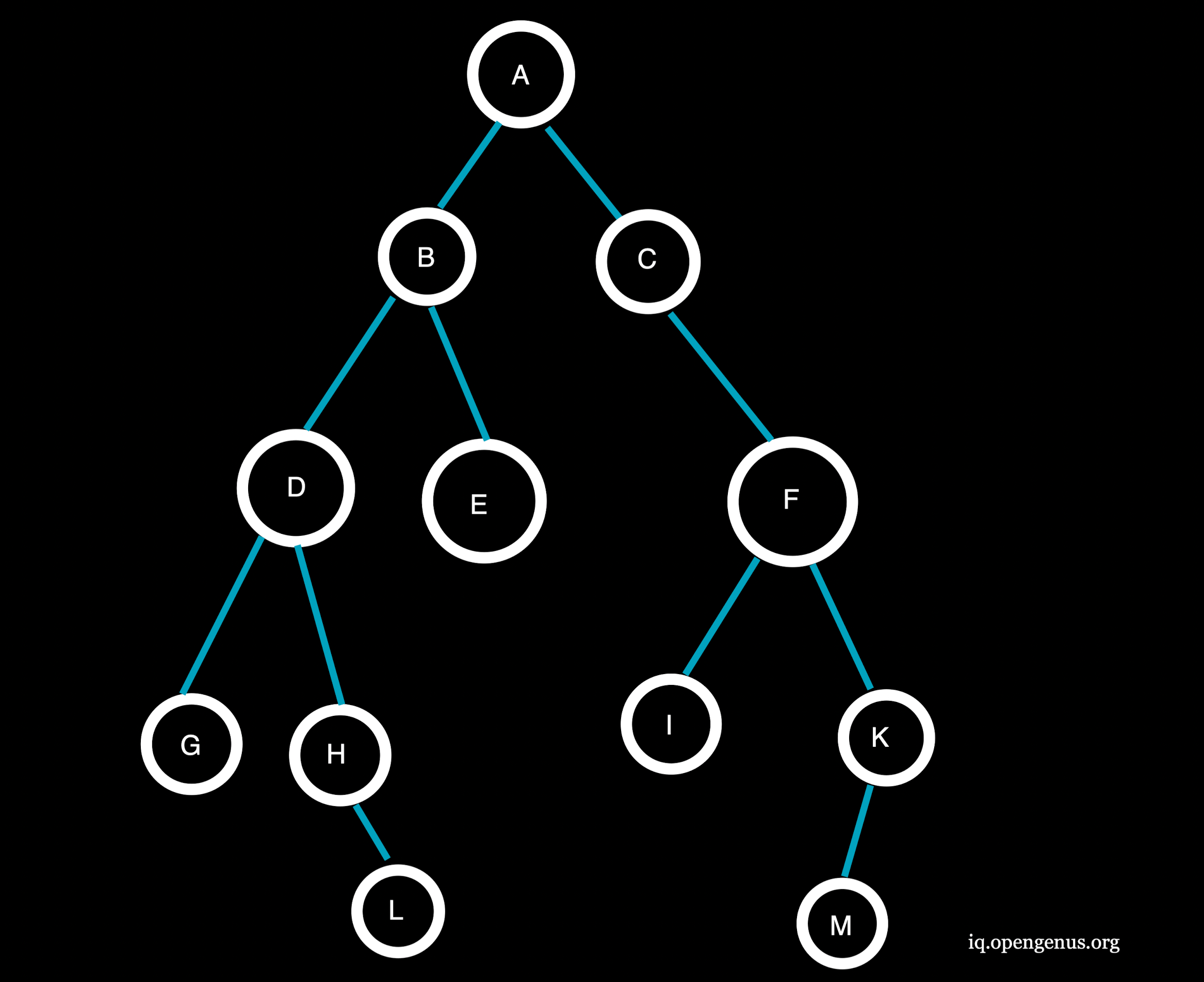
Consider the given graph with Depth Limit(l)=2, Target Node=H and the given source node=A
Step 1 :
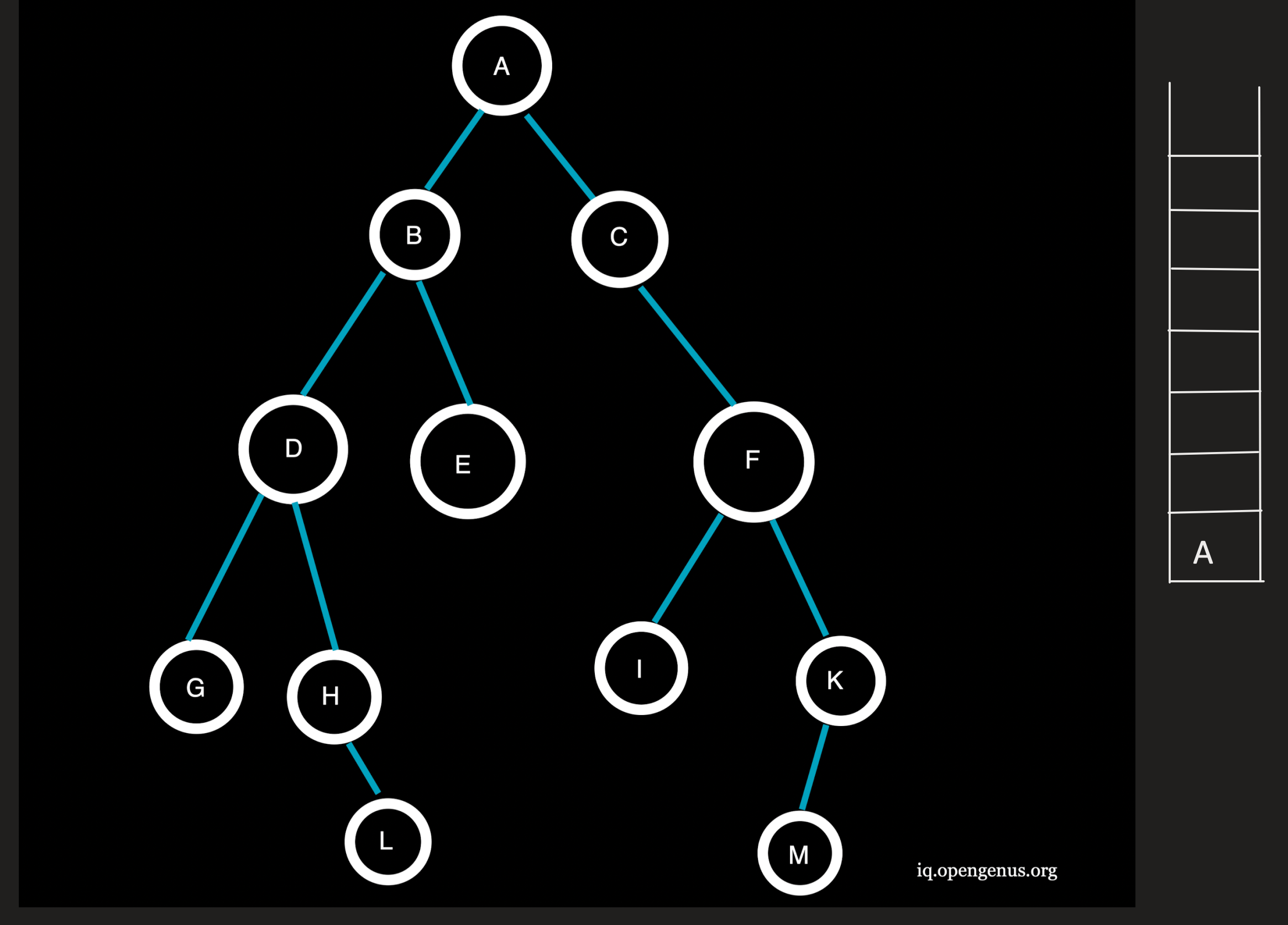
Now, the first element of the source node is pushed onto the stack.
Step 2 :
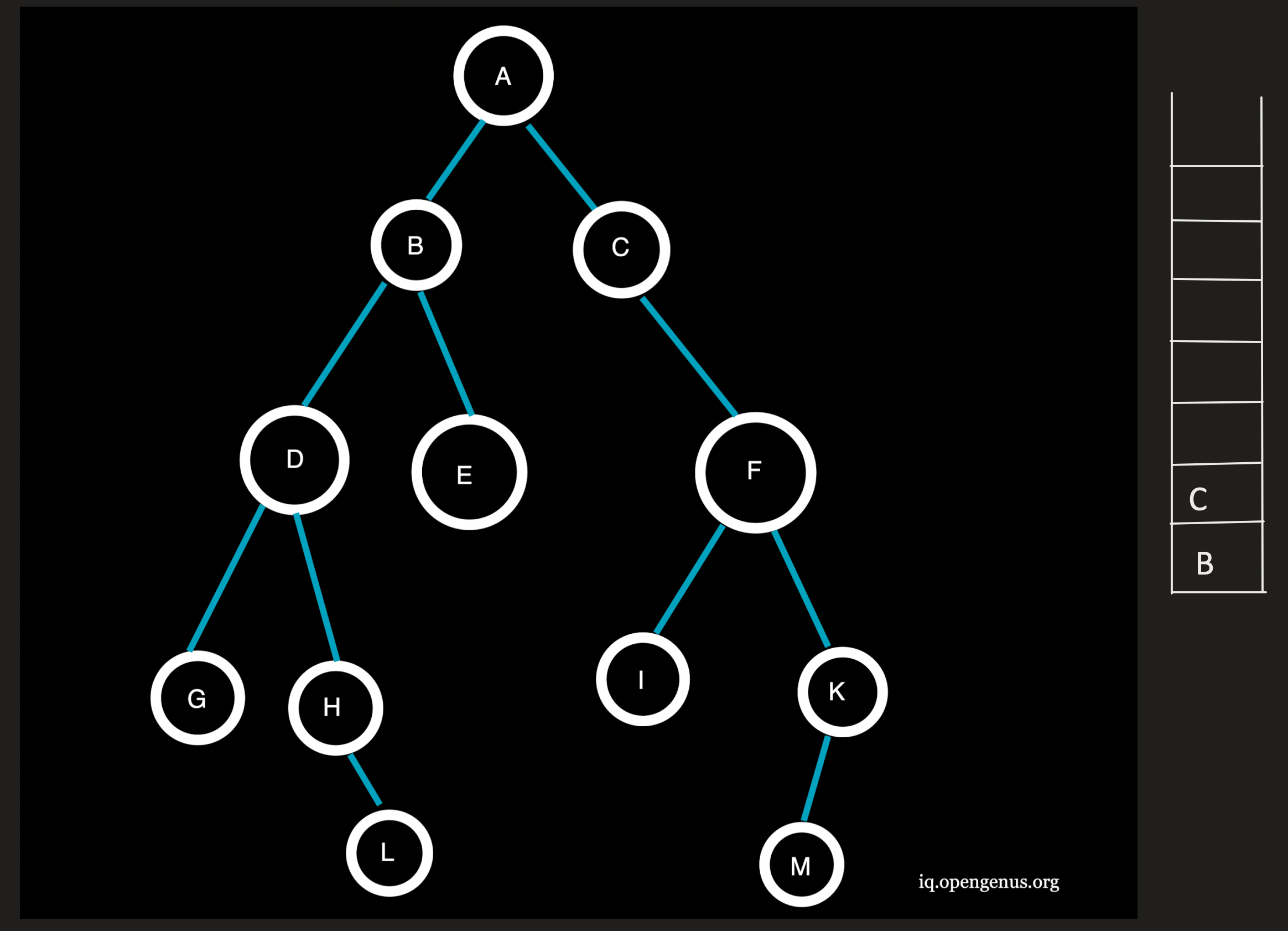
A being the top element is now popped from the stack and the neighbouring nodes B and C at depth=1(<l) of A are pushed onto the stack.
Traversal: A
Step 3 :
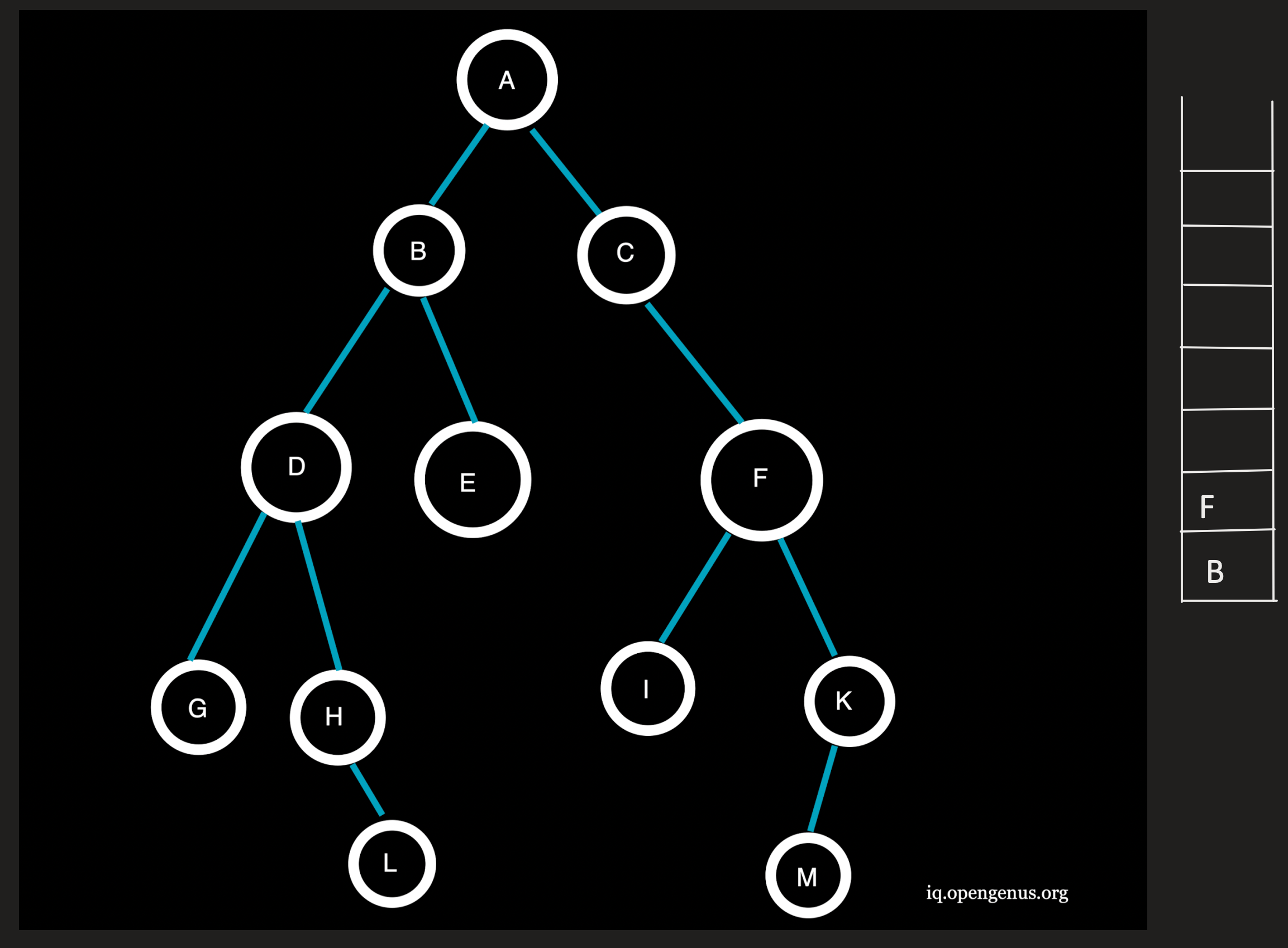
C being the topmost element is popped from the stack and the neighbouring node F at depth=2(=l) is pushed onto the stack.
Traversal: AC
Step 4 :
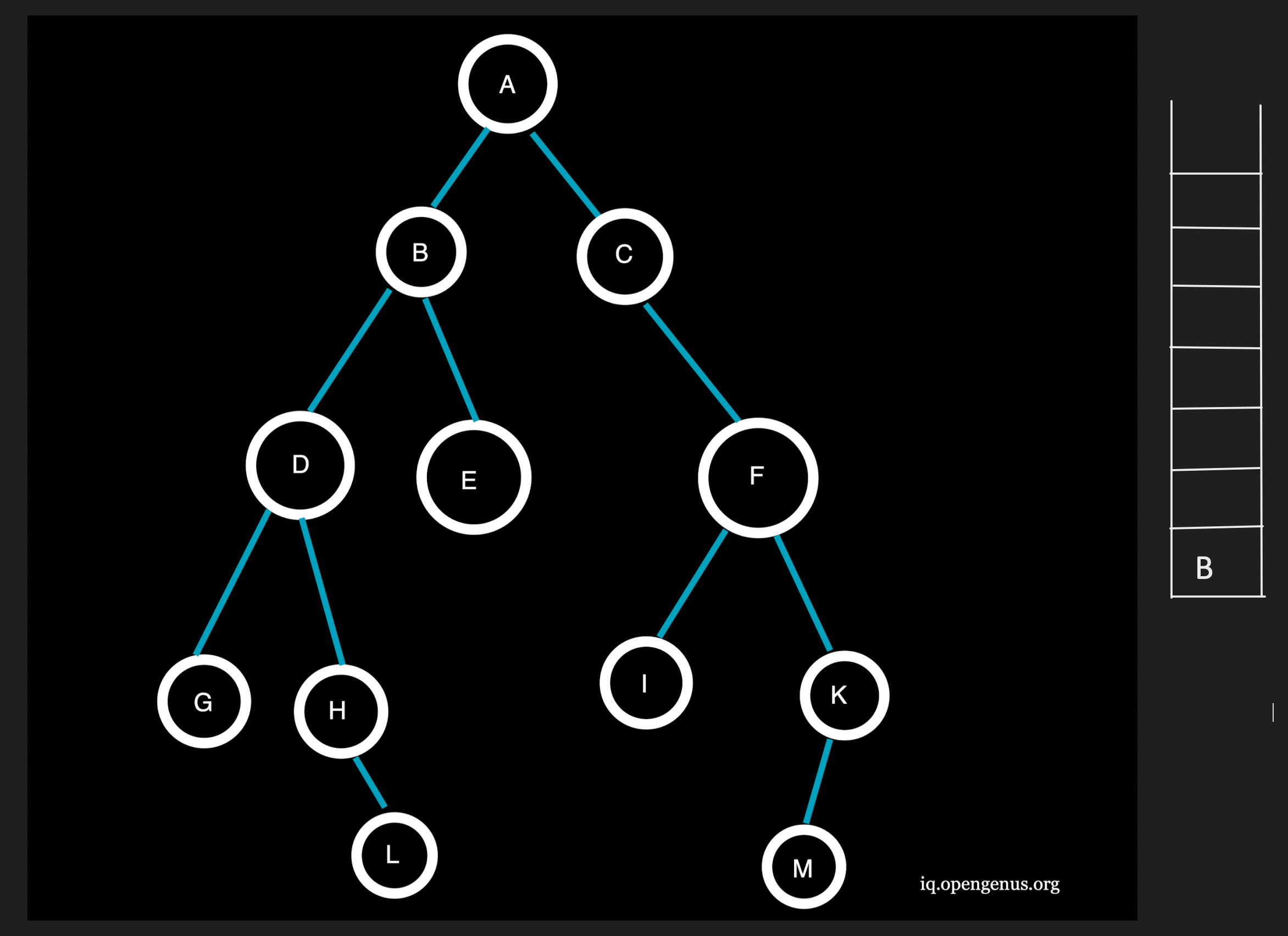
F being the topmost element is popped from the stack and the neighbouring nodes I and J at depth=3(>l) will not be pushed onto the stack.
Traversal: ACF
Step 5 :
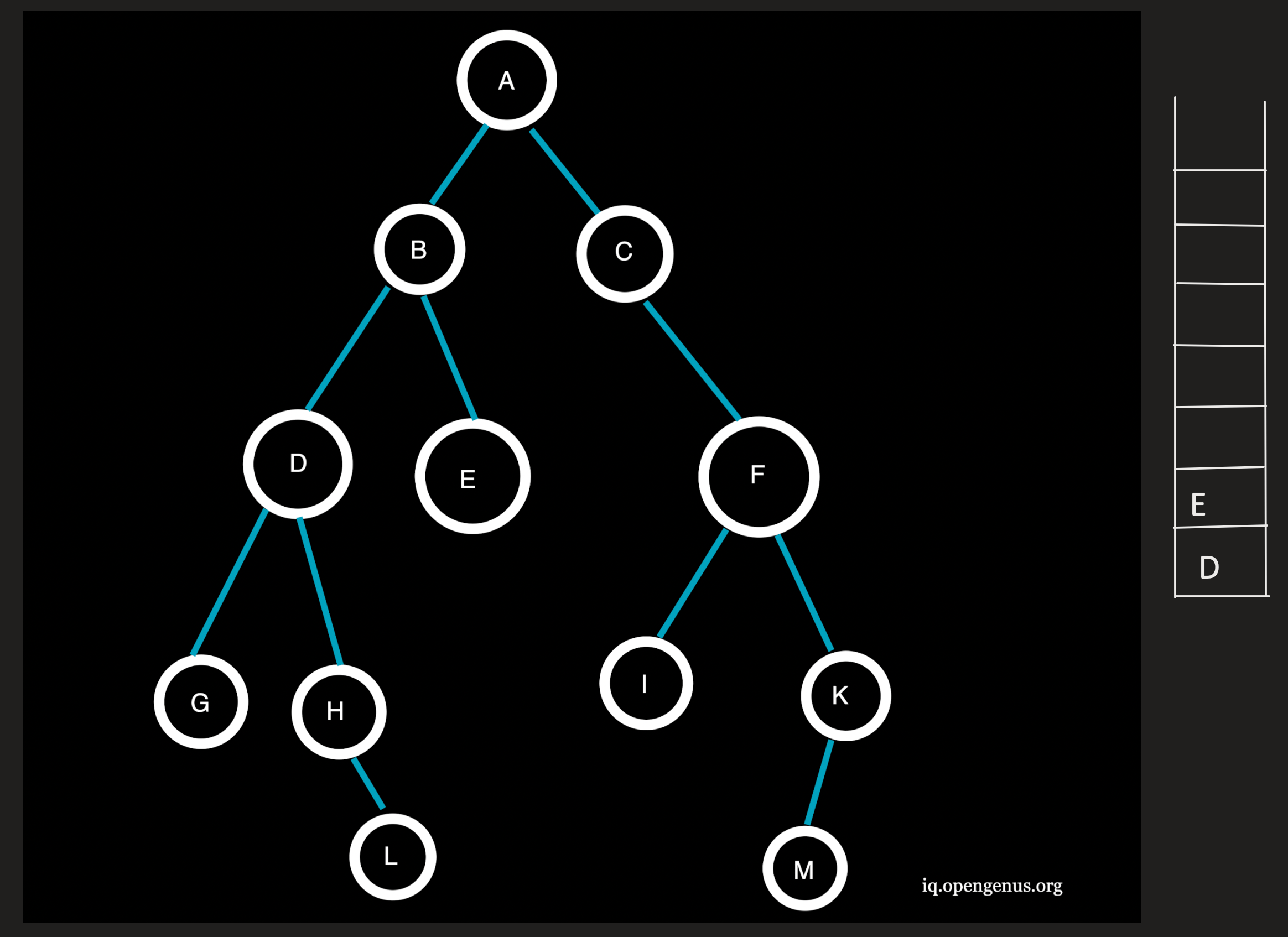
B being the topmost element is popped from the stack and the neighbouring nodes D and E at depth=2(=l) are pushed onto the stack.
Traversal: ACFB
Step 6 :
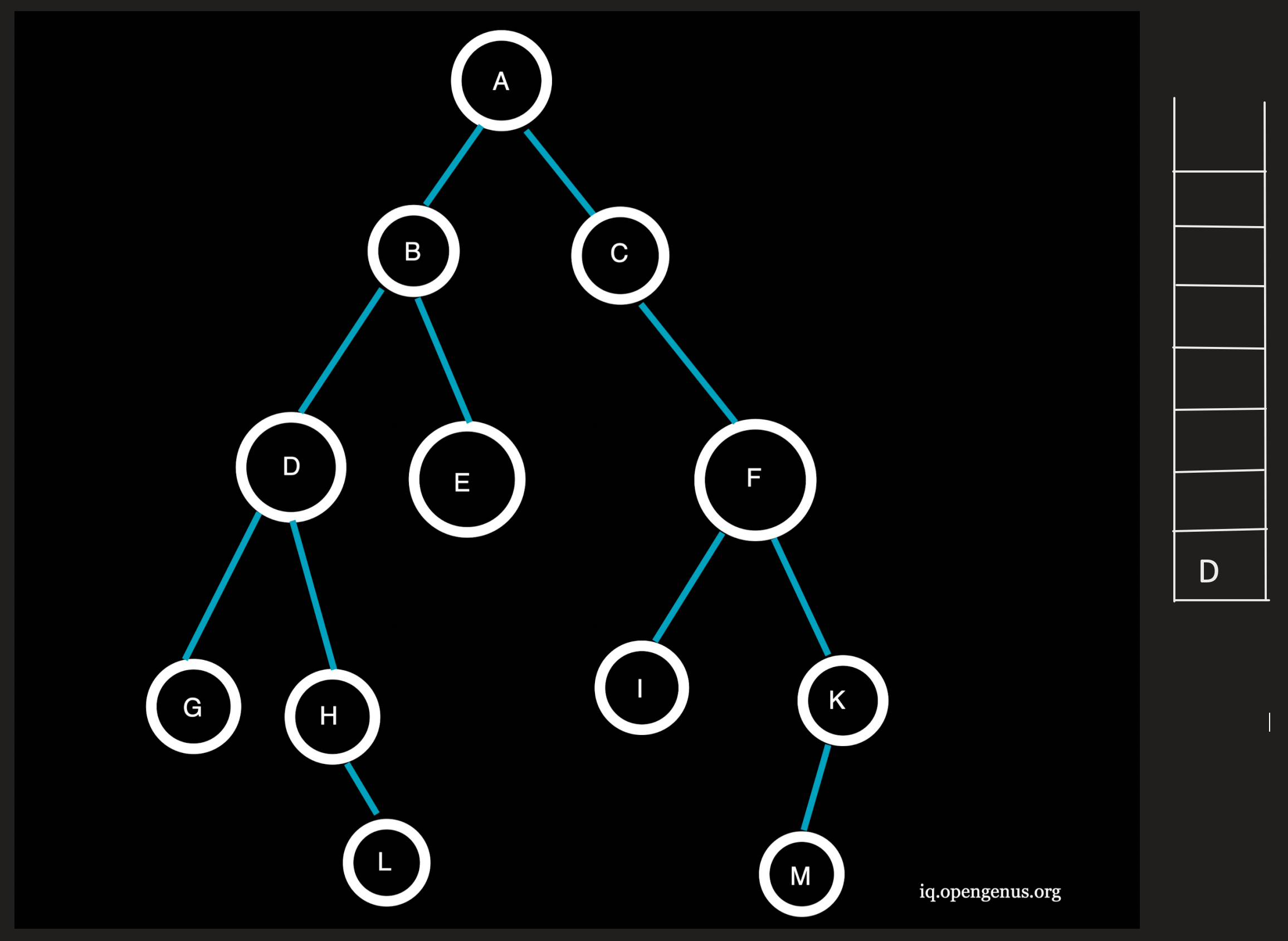
E being the topmost element is popped from the stack and since E has no neighbouring nodes, no nodes are pushed onto the stack.
Traversal: ACFBE
Step 7 :
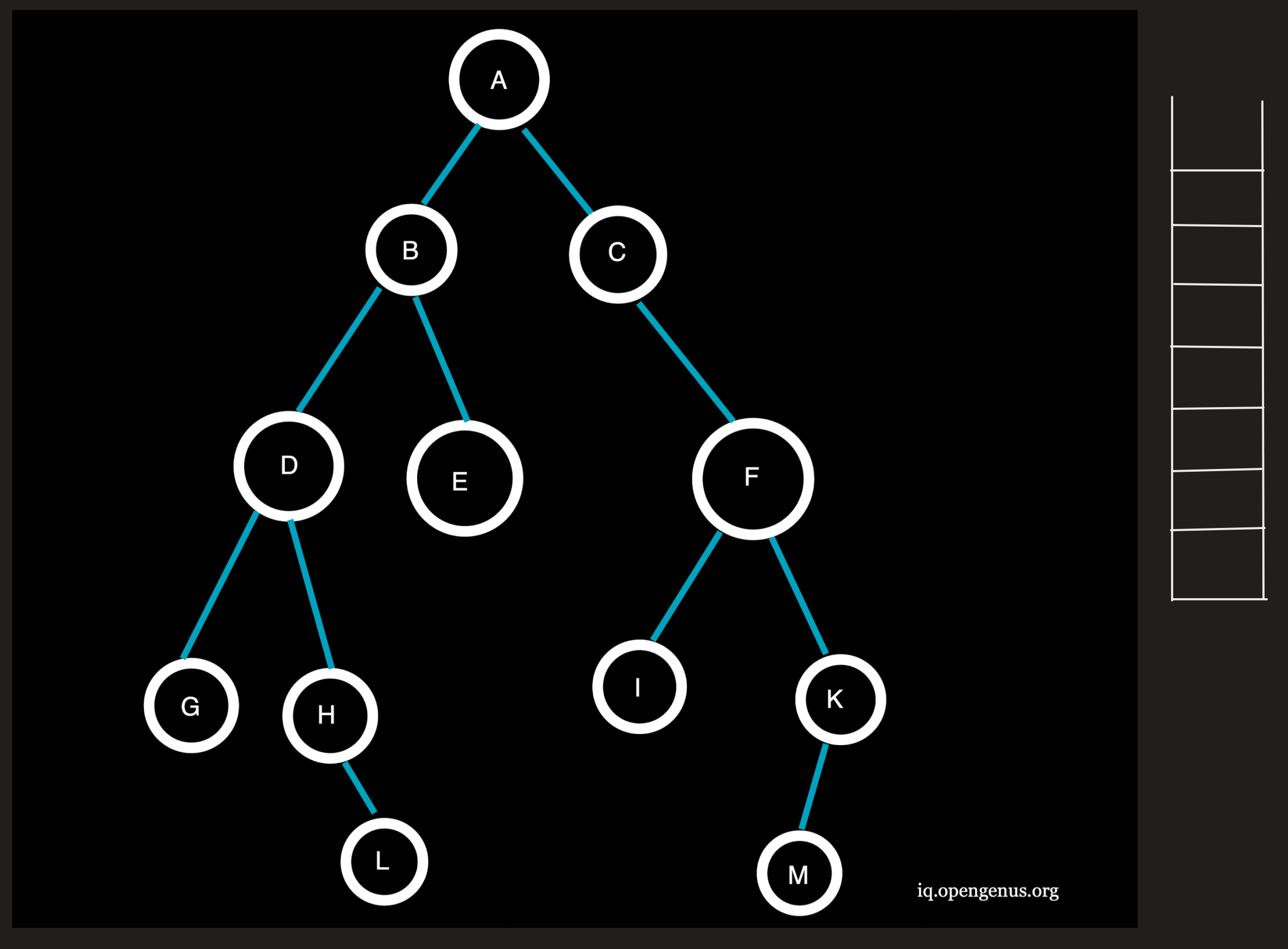
D being the topmost element is popped from the stack and the neighbouring nodes G and H at depth=3(>l) will not be pushed onto the stack.
Traversal: ACFBED
Since the stack is now empty, all nodes within the depth limit have been visited, but the target node H has not been reached.
Implementation
An implementation of the DLS class as an extension of the Abstract java class
Abstract Java Class:
/**
* Abstract.
*/
public abstract class Abstract {
Node sourceNode;
Node goalNode;
public AbstractSearch(Node sourceNode, Node goalNode){
this.sourceNode = sourceNode;
this.goalNode = goalNode;
}
public abstract boolean execute();
}
DLS Class:
import java.util.ArrayList;
import java.util.Stack;
/**
* Depth Limited Search Class
*/
public class DLS extends Abstract {
Node sourceNode;
Node goalNode;
int depth = 0;
int limit = 2;
public DLS(Node source, Node goalNode){
super(source, goalNode);
this.sourceNode = source;
this.goalNode = goalNode;
}
public boolean execute(){
Stack<node> nodeStack = new Stack<>();
ArrayList<node> visitedNodes = new ArrayList<>();
nodeStack.add(sourceNode);
depth = 0;
while(!nodeStack.isEmpty()){
if(depth <= limit) {
Node current = nodeStack.pop();
if (current.equals(goalNode)) {
System.out.print(visitedNodes);
System.out.println("Goal node found");
return true;
} else {
visitedNodes.add(current);
nodeStack.addAll(current.getChildren());
depth++;
}
} else {
System.out.println("Goal Node not found within depth limit");
return false;
}
}
return false;
}
}
Advantages of Depth Limited Search
1.Depth limited search is more efficient than DFS, using less time and memory.
2.If a solution exists, DFS guarantees that it will be found in a finite amount of time.
3.To address the drawbacks of DFS, we set a depth limit and run our search technique repeatedly through the search tree.
4.DLS has applications in graph theory that are highly comparable to DFS.
Disadvantages of Depth Limited Search
1.For this method to work, it must have a depth limit.
2.If the target node does not exist inside the chosen depth limit, the user will be forced to iterate again, increasing execution time.
3.If the goal node does not exist within the specified limit, it will not be discovered.
Measures of Performance
Completeness: DLS search algorithm is complete if the solution is above the depth-limit.
Time Complexity: Time complexity of DLS algorithm is O(b^l) where b is known as the branching factor (number of children at each node) and l is the given depth limit.
Space Complexity: Space complexity of DLS algorithm is O(bxl) where b is known as the branching factor (number of children at each node) and l is the given depth limit.
Optimal: Even if l>d, depth-limited search is not ideal.
Comparison of DLS with BFS and DFS
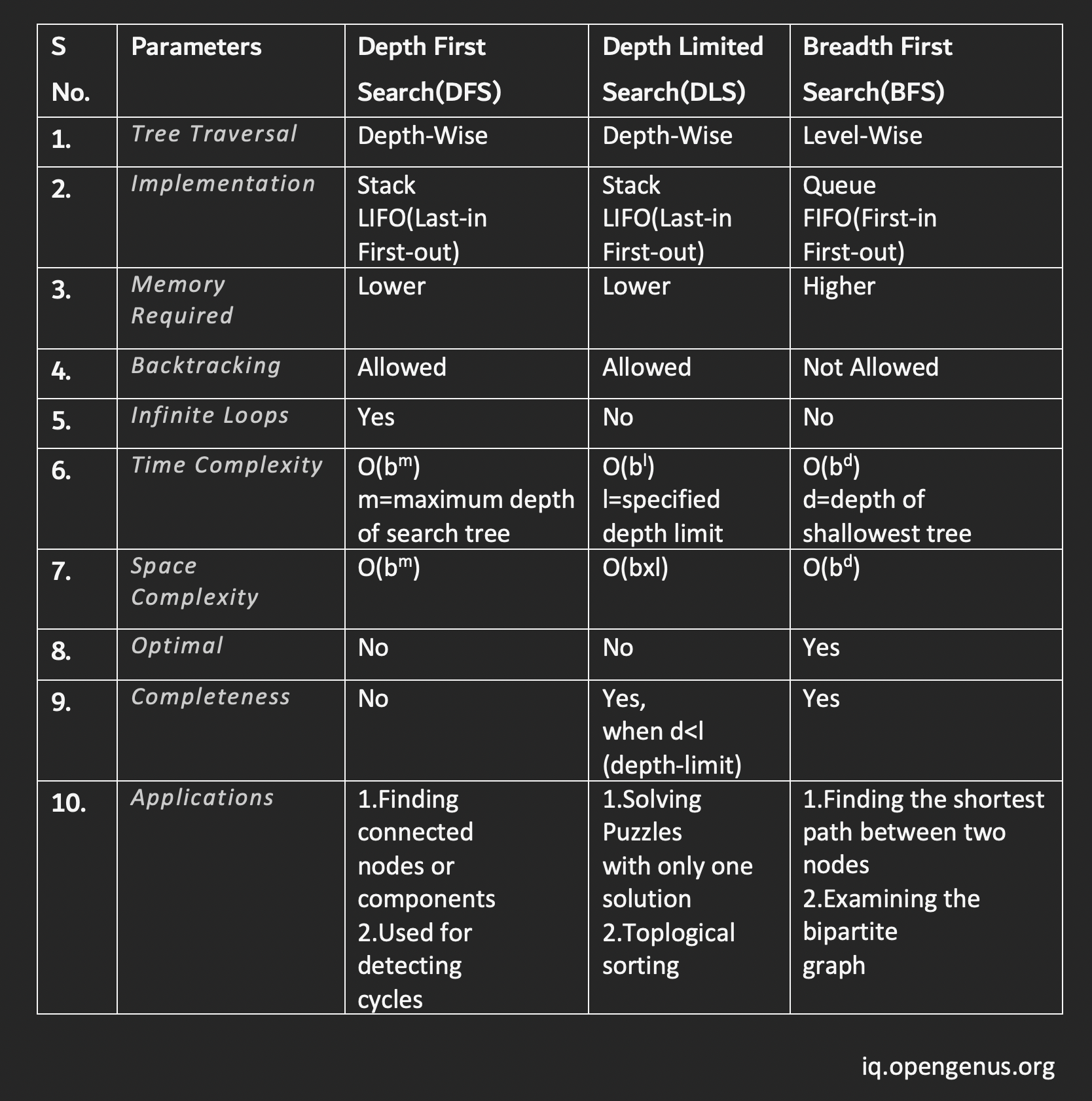
Conclusion
When we know the search domain and have previous knowledge of the problem and its domain, we apply the DLS algorithm, which is not the case with an uninformed search strategy. Unless someone has attempted and solved the problem before, we usually have almost no idea of the depth of the destination node.
