
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Table of Contents
- Introduction to Bentley Ottmann Algorithm for Plane Sweeping
- Binary Search Tree
- Priority Queue
- Algorithm
- Implementation
- Analysis
- Overview
Introduction to Bentley Ottmann Algorithm for Plane Sweeping
In this article, we shall be discussing the Bentley-Ottmann algorithm for computing a plane sweep. This lists all the intersection points in a set of line segments. The Bentley-Ottman algorithm takes O((n+k)logn) time where k = o(n^2/logn), it makes the algorithm more efficient than a standard naive approach which would take O(n^2) by checking every pair of segments.
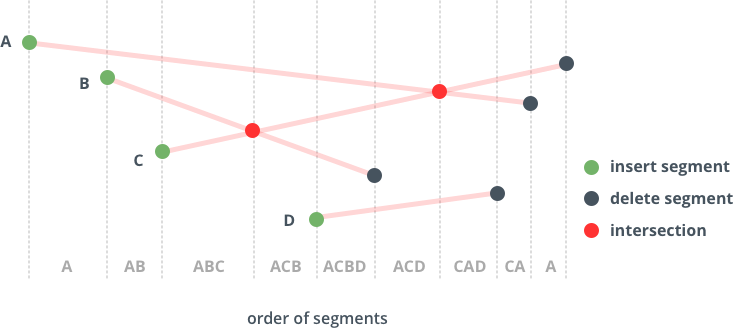
Put simply, the Bentley-Ottmann algorithm sweeps across the given plan using a line. That said, a vertical line (let's call it L) will sweep across the plan horizontally or vertically, intersecting the input line segments in sequence as it move across. Generally, we can say:
- No two line segment endpoints or crossings have the same x-coordinate
- No line segment endpoint lies upon another line segment
- No three line segments intersect at a single point
When this is the case, line L will always intersect the input line segments in a set of points whose vertical ordering changes only at a set of discrete events. An event could be associated with an endpoint (far left or far right of a line) or an intersection point of two line segments. This means that the motion of line L can be decomposed into a finite sequence, and therefore simulated by an algorithm.
The outcome of the simulation has two possibilities. When our line sweeps across an endpoint of a segment, the intersection of L with the segment is added to/removed from the vertically ordered set of intersection points. We can predict this as the end points are known from the input to the algorithm. The other possibility is when L sweeps across an intersection of two line segments. We know this will happen if both the intersection points between L and each of the segments are adjacent in the vertical ordering of the intersection points.
To maintain the intersection points of the sweeping line L with the input line segments, the Bentley-Ottmann algorithm maintains two data structures:
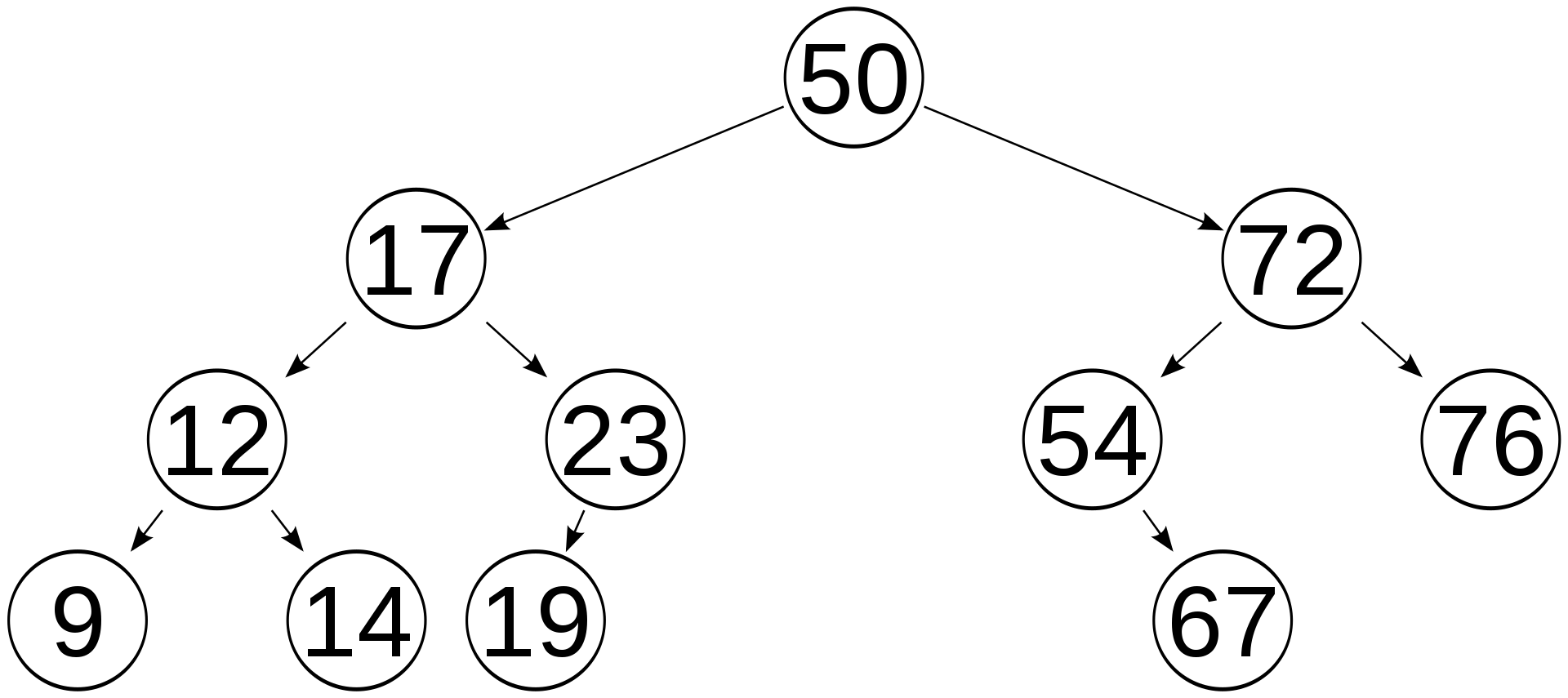
Binary Search Tree
The tree contains the set of input line segments which intersect with L, ordered by the y-coordinate of the intersection points. The points themselves however are not explicitly represented in the BST. A segment will be inserted into the tree when our sweep line crosses the left end point of the segment. The position of the segment can be computed with a binary search, which tests whether the endpoint is above or below another segment which is intersected by L. This means that an intersection can be done in logarithmic time. The algorithm can also delete segments from the BST, then use the tree to determine the segments that are immediately above or below others. It can be done entirely in the tree and does not need the geometry of the segments.
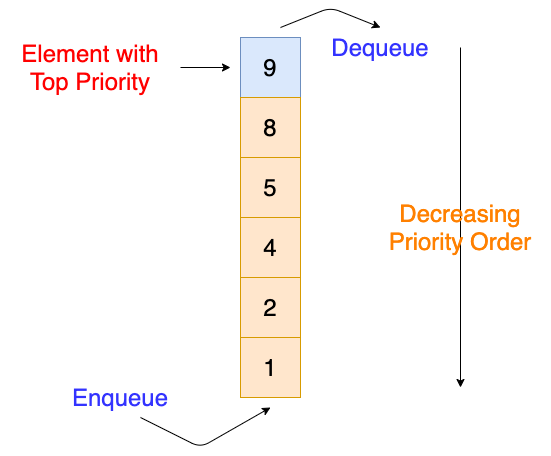
Priority Queue
The second data structure used in the algorithm is a priority queue. The queue is used to maintain a potential sequence of future events in the algorithm. As described in the introduction, each event can either be related to when the line sweeps across an endpoint of a segment or an intersection point. The event happens when L sweeps over the left endpoint of a segment, meaning the events can be prioritised with respect to the x-coordinates of the points that are associated. The possible future events consist of the line segment endpoints which have not yet been swept and the intersection points of lines containing pairs of segments which are immediately above or below each other.
Algorithm
Having learned the principles of the algorithm, we can now formulate it into a computational approach.
- Initialise a priority queue (Q) of possible future events, each of which are associated with a point in the plane and are prioritised by x-coordinate. Meaning that initially, Q contains an event for each endpoint of the input segments.
- Initialise a self-balancing BST (T) of the line segments which intersect with our sweep line (L). This is ordered by y-coordinate of the intersection points. Initially T is empty.
- While Q is not empty, find and remove the event from Q associated with the point that has the minimum x-coordinate and determine the event type. Then, we can proceed in three ways:
- If the point (P) is the left endpoint of the given line segment (S), insert S into T. Find the line segments which are immediately above and below S in T if they exist (r and t). If the intersection of the segments forms a possible future event in the priority queue, remove the event. If origin line segment intersects the ones above or below it, add the intersection points to the queue of possible future events.
- If P is the right endpoint of S, remove S from T. Find the line segments that are immediately above and below S (prior to S's removal) in T if it exists. If these segments intersect, add the intersection point as a possible future event in the queue.
- If P is an intersection point of two segments (where S is below t), swap their positions in T. After swapping find segments r and u (if exist) that are immediately below and above t and s, respectively. Remove any intersection points r-s and t-u from the queue. If r and t cross or s and u cross, add the intersection points to the queue
Implementation
Here is an implementation of the algorithm in Python
Note: Q and T are standard priority queue and BST classes
Algorithm implementation
from Q import Q
from T import T
from helper import *
ev = 0.00000001
# to determine which is the furthest right/left
lower_check = 100
# get the next point (eg. point with lower y-coordinate)
def getNextPoint(p, seg, y_lower):
p1 = seg[0]
p2 = seg[1]
if (p1[0]-p2[0])==0:
return (p[0]+10, p[1])
slope = float(p1[1]-p2[1])/(p1[0]-p2[0])
if slope==0:
return (p1[0], p[1]-y_lower)
y = p[1]-y_lower
x = p1[0]-(p1[1]-y)/slope
return (x, y)
"""
for each event point:
U_p = segments that have p as an upper endpoint
C_p = segments that contain p
L_p = segments that have p as a lower endpoint
"""
def handle_event_point(p, segs, q, t, intersections):
rightmost = (float("-inf"), 0)
rightmost_seg = None
leftmost = (float("inf"), 0)
leftmost_seg = None
U_p = segs
(C_p, L_p) = t.contain_p(p)
merge_all = U_p+C_p+L_p
if len(merge_all) > 1:
intersections[p] = []
for s in merge_all:
intersections[p].append(s)
merge_CL = C_p+L_p
merge_UC = U_p+C_p
for s in merge_CL:
# deletes at a point slightly above (to break ties) - where seg is located in tree
# above intersection point
t.delete(p, s)
# put segments into T based on where they are at y-val just below p[1]
for s in merge_UC:
n = getNextPoint(p, s, lower_check)
if n[0] > rightmost[0]:
rightmost = n
rightmost_seg = s
if n[0] < leftmost[0]:
leftmost = n
leftmost_seg = s
t.insert(p, s)
# means only L_p -> check newly-neighbored segments
if len(merge_UC) == 0:
neighbors = (t.get_left_neighbor(p), t.get_right_neighbor(p))
if neighbors[0] and neighbors[1]:
find_new_event(neighbors[0].value, neighbors[1].value, p, q)
# of newly inserted pts, find possible intersections to left and right
else:
left_neighbor = t.get_left_neighbor(p)
if left_neighbor:
find_new_event(left_neighbor.value, leftmost_seg, p, q)
right_neighbor = t.get_right_neighbor(p)
if right_neighbor:
find_new_event(right_neighbor.value, rightmost_seg, p, q)
def find_new_event(s1, s2, p, q):
i = intersect(s1, s2)
if i:
if compare_by_y(i, p) == 1:
if not q.find(i):
q.insert(i, [])
# segment ((x, y), (x, y)) form
# first part in segment should have higher y-coordinate
def intersection(S):
s0 = S[0]
if s0[1][1] > s0[0][1]:
s0 = (s0[1], s0[0])
q = Q(s0[0], [s0])
q.insert(s0[1], [])
intersections = {}
for s in S[1:]:
if s[1][1] > s[0][1]:
s = (s[1], s[0])
q.insert(s[0], [s])
q.insert(s[1], [])
t = T()
while q.key:
p, segs = q.get_and_del_min()
handle_event_point(p, segs, q, t, intersections)
return intersections
Helper functions
ev = 0.0000001
# floating-point comparison
def approx_equal(a, b, tol):
return abs(a - b) < tol
# ordering of tree
def compare_by_x(k1, k2):
if approx_equal(k1[0], k2[0], ev):
return 0
elif k1[0] < k2[0]:
return -1
else:
return 1
# priority of Q
def compare_by_y(k1, k2):
if approx_equal(k1[1], k2[1], ev):
if approx_equal(k1[0], k2[0], ev):
return 0
elif k1[0] < k2[0]:
return -1
else:
return 1
elif k1[1] > k2[1]:
return -1
else:
return 1
# tests if s0 and s1 represent the same segment (i.e. pts can be in 2 different orders)
def segs_equal(s0, s1):
x00 = s0[0][0]
y00 = s0[0][1]
x01 = s0[1][0]
y01 = s0[1][1]
x10 = s1[0][0]
y10 = s1[0][1]
x11 = s1[1][0]
y11 = s1[1][1]
if (approx_equal(x00, x10, ev) and approx_equal(y00, y10, ev)):
if (approx_equal(x01, x11, ev) and approx_equal(y01, y11, ev)):
return True
if (approx_equal(x00, x11, ev) and approx_equal(y00, y11, ev)):
if (approx_equal(x01, x10, ev) and approx_equal(y01, y10, ev)):
return True
return False
# get gradient of a given segment
def get_slope(s):
x0 = s[0][0]
y0 = s[0][1]
x1 = s[1][0]
y1 = s[1][1]
if (x1-x0)==0:
return None
else:
return float(y1-y0)/(x1-x0)
# given a point p, return the point on s that shares p's y-val
def get_x_at(s, p):
m = get_slope(s)
if m == 0: # horizontal segment
return p
if m is None: # vertical segment
return (s[0][0], p[1])
x1 = s[0][0]-(s[0][1]-p[1])/m
return (x1, p[1])
# Returns intersection point of two segments, or none if doesn't exist
def intersect(seg1, seg2):
p = seg1[0]
r = (seg1[1][0]-seg1[0][0], seg1[1][1]-seg1[0][1])
q = seg2[0]
s = (seg2[1][0]-seg2[0][0], seg2[1][1]-seg2[0][1])
denom = r[0]*s[1]-r[1]*s[0]
if denom == 0:
return None
numer = float(q[0]-p[0])*s[1]-(q[1]-p[1])*s[0]
t = numer/denom
numer = float(q[0]-p[0])*r[1]-(q[1]-p[1])*r[0]
u = numer/denom
if (t < 0 or t > 1) or (u < 0 or u > 1):
return None
x = p[0]+t*r[0]
y = p[1]+t*r[1]
return (x, y)
Analysis of Algorithm
The algorithm can process one event per segment endpoint or intersection point, in order sorted by x-coordinate of these points since it may be proved by induction. Once the ith event has been processed, the next event (if it is an intersection point) must be an intersection of two segments that are adjacent in the ordering of the segments in our BST, because the algorithm maintains all the intersections between adjacent segments as possible future events in Q, the correct next event will always be present in the queue, meaning it will correctly find all the intersections of the input points.
The algorithm will process 2n+k events where n is the number of inputted line segments and k is the number of crossings. Each event is processed by a a constant number of BST and queue operations. Since the queue only contains segment endpoints and crossings between adjacent segments, it will not exceed more than 3n events. All given operations will take O(logn) to complete and therefore giving us the total time complexity of O((n+k)logn).
Overview
In this article we have covered the Bentley-Ottmann algorithm for computing all the intersections of a set of line segments by using the plane-sweeping technique. I have described the general theory behind the algorithm, the data structures used, the computational approach and implementation before finally analysing this to get both the proof that the algorithm works, and its time complexity.
