In this article, we have explained Applications of Computational Geometry along with topics/ algorithms used to solve a specific problem.

Table of Contents

• Introduction
• Applications/Algorithms
  • Rendering/Simulations
  • Artificial Intelligence
  • Networking
  • Linear Programming
  • GIS
• Overview

Introduction

In this article, we shall introduce the concept of computational geometry, this will build on all of the geometric we have established previously and apply it in a computational perspective. We can say that computational geometry is the use of algorithms that can be presented in a geometric context. These algorithms are used throughout many fields including robot movement planning, geographic information systems (GIS), network design and more. We shall present some example problems, and then show how we can use computational geometry to solve them.

Applications/Algortihms

I will now briefly explain some places where computational geometry can be used, highlighting the great potential within the field.

Rendering/Simulations

Computational geometry is largely the reason why we can create physical simulations or render objects in programs such as Blender at all. For example, mesh generation is used in rendering which is based on Delaunay triangulation, this can be implemented in the form of algorithms such as divide and conquer or Ruppert's algorithm. Meshes can be used in a variety of different things but as mentioned above, are especially useful for things such as 3D VFX or for physical simulations such as finite element analysis or computational fluid dynamics. Many different rendering techiques such as rasterization or ray casting all have their roots in compuatational geometry, in more recent times ray tracing technology has become at the forefront of the gaming industry through an emphasis by companies such as NVIDIA.

Artificial Intelligence

Another field where computational geometry is prevelant is artifical intelligence, when finding optimal paths for travel, geometric algorithms are quintessential. For example, A* pathfinding can be used to find the shortest path from a start and end goal. This uses a grid-based approach and heuristics, which are a basic form of machine learning which means that a better path will be found, the more experience the algorithm has. To check if the path is clear, a voronoi diagram can be used as, if its points are obstacles, it means that its edges are the routes furthest from said obstacles and therefore theoretically furthest from collisions. Another place where we have seen computational geometry in the AI field is through computer vision, for example, convex hulls are used widely in self-driving cars or facial recognition as it allows the data which the algorithm is recieving through the camera to be interpretted more consistently and in a way which it can actually learn from, for example, a convex-hull of a car is a lot easier to use in object avoidence than a normal mesh, cars come in many shapes and have many contours or bumps, placing them within a convex hull allows for a more consistent and uniform shape to be used, improving the algorithm.

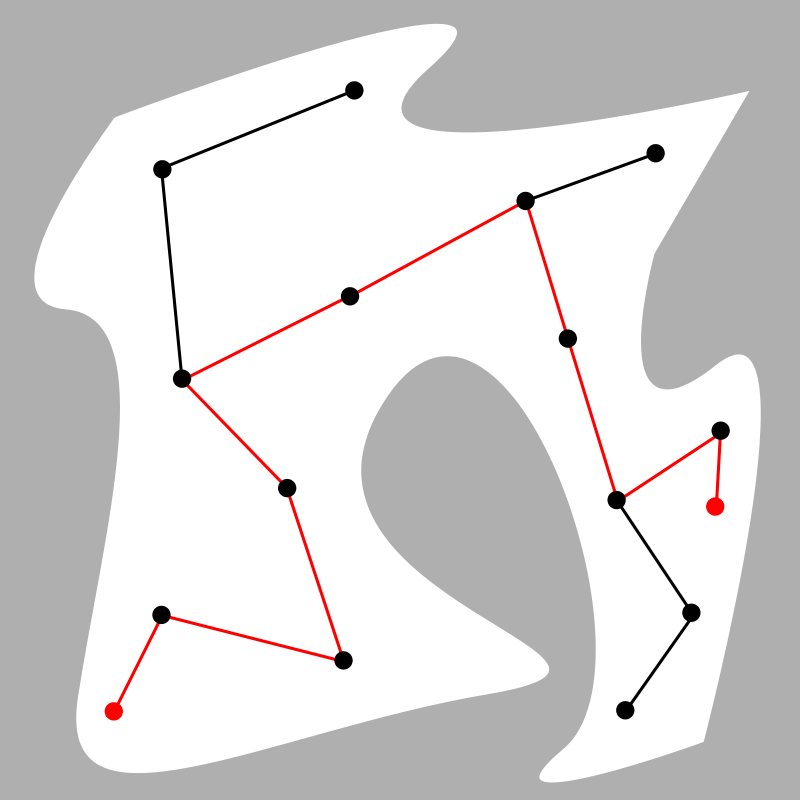
Networking

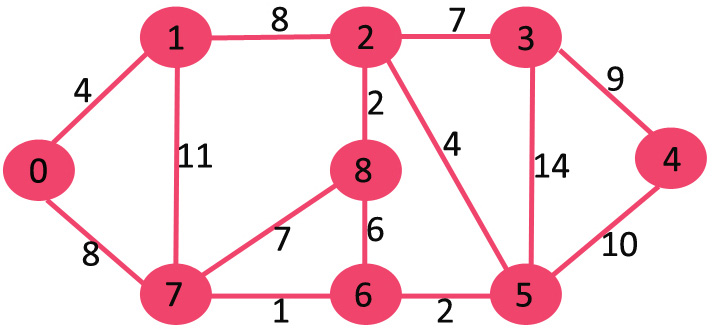
Networking is another field where computational geometry is paramount. For example, shortest-path algorithms such as Dijkstra's are used in directing router traffic, it is almost a perfect use case for this, each edge (connection to another router) will have a different cost based on the current traffic, therefore an algorithm such as Dijkstra's can be used in order to compute the shortest distance for the packets to travel. In other optimisations, a voronoi diagram can be used in order to map the maximum capacity for a wireless network, allowing the engineer to know where best to put each node/switch etc.

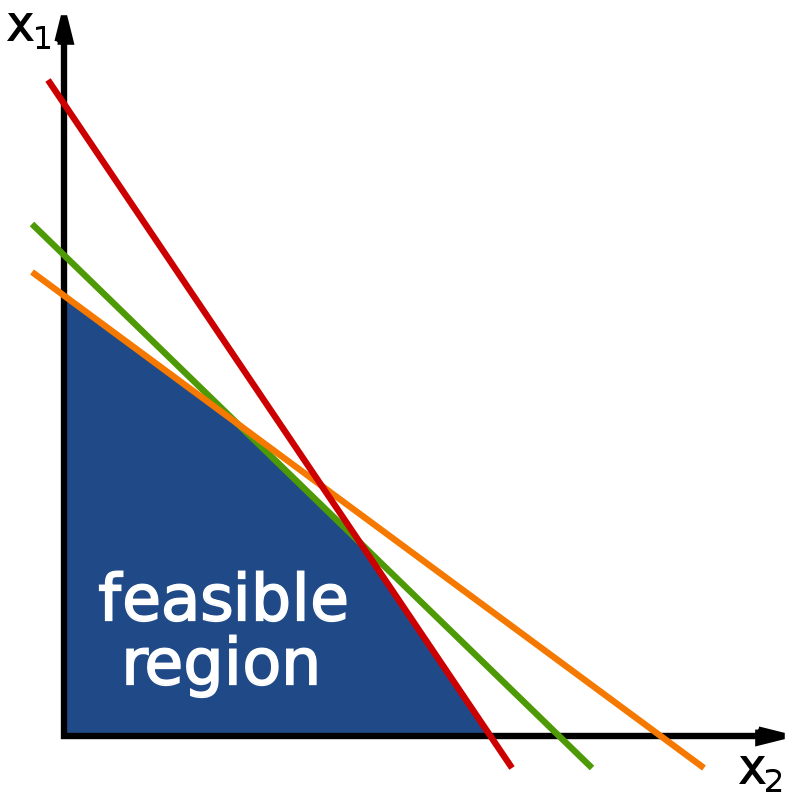
Linear Programming

Computational geometry is used widely throughout linear programming, this is a way of formulating real-world problems into mathematical models and then optimising it. For example, the simplex algorithm can solve linear programming problems by constructing a feasible solution based on some constraints, this series will produce a convex region of possible values for the given variables, for example, it may be in the shape of a simple polygon. We then traverse the edges of the shape, to the vertices with non-decreasing values of the function until the optimal output is reached. Linear programming has applications in industries such as agriculture and transportation, for example, any public transport routes will have been optimised through linear programming methods for cost and time efficiency.

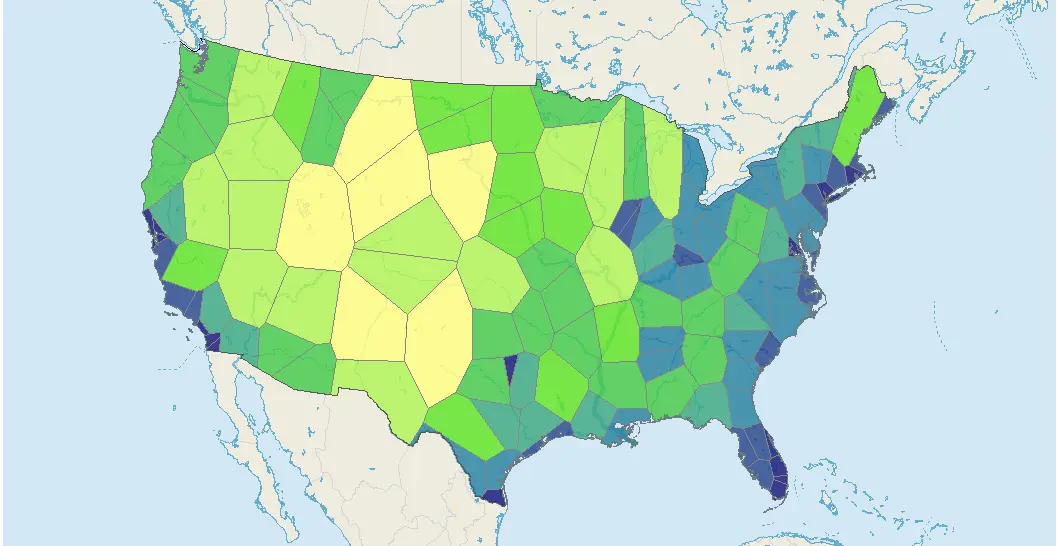
Geographic Information Systems

Many of the problems that are to be solved in GIS are geometric problems, it is only natural to have included computational geometry in the development of these systems. It is used prevelantly throught any modern GIS software (such as Google Maps or ArcGIS) for processes such as data correction, data retrieval, analysis and visualisation. Within spatial data analysis, any patterns, clusters or outliers are to be detected. In a given software, an outlier may be defined as many different things, but generally, it is a point or points that are further away by some defined distance from all other points. For example, if we define a point as an outlier if its fifth-closest point is further away than a given distance, we can use higher-order voronoi diagrams to determine this efficiently.

Overview

In this article at OpenGenus we have covered the basics of computational geometry, explaining what it is and then showing a range of different ways that it can be used to solve problems, explaining numerous applications, and how computational geometry is used to help solve them.