In this article, we have explored the Section formula in Computational Geometry which deals with straight lines getting divided in a given ratio. This is an important concept.

Table of contents

• Introduction
• Internal Division
• External Division
• Special Case - Midpoint
• Overview

Introduction

In this article we shall cover the section formula, its uses and problems to solve using it. We will first introduce it in simple cases where a point divides a line in a given ratio and then delve into more complex problems surrounding internal and external division. This will give a strong foundation into coordinate geometry and show a common formula which will become useful in many cases in the future.

Dividing point in a given ratio

Firstly we will cover how to calculate a point which divides a line by a given ratio. We can formalise this by saying, given coordinate points (x1,y1), (x2,y2) and m and n. Find the point that divides (x1,y1) and (x2,y2) in the given ratio m:n. The formula has two forms based on whether the point divides the line internally or externally, we will explain and derive both below.

Examples

Points: (1,0) (2,5)
M,N = 1

Output: (1.5, 2.5) as divides line with the ratio 1:1

Points: (2,4) (4,6)
M = 2,N = 3

Output: (2.8,4.8) as divides the line with the ratio 2:3

Internal Division

For internal division, we can formalise this by expressing it as the equation:

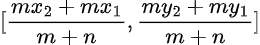
Derivation

We shall first derive the sectional formula for an internal point. We can do this through use of the example below:

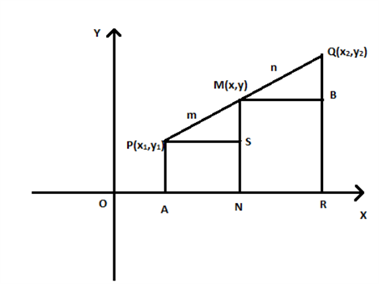
PA, MN and QR are perpendicular to the x-axis whilst PS and MB are parallel.
∠MPS is equal to ∠QMB through correspondence, they both equal 90 degrees
Through Angle-Angle similarity criterion, ΔPMS ~= ΔMQB

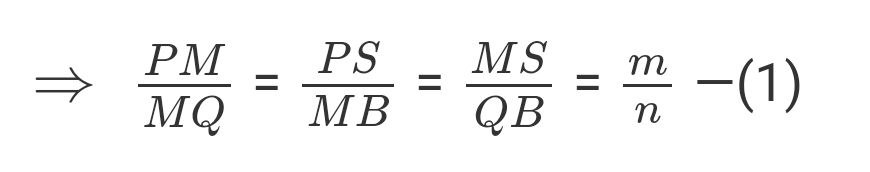
PS = AN = ON - OA = x - x1
MB = NR = OR - ON = x2 - x
MS = MN - MS = y - y1
QB = RQ - RB = y2 - y

From this, we can form the equations below:

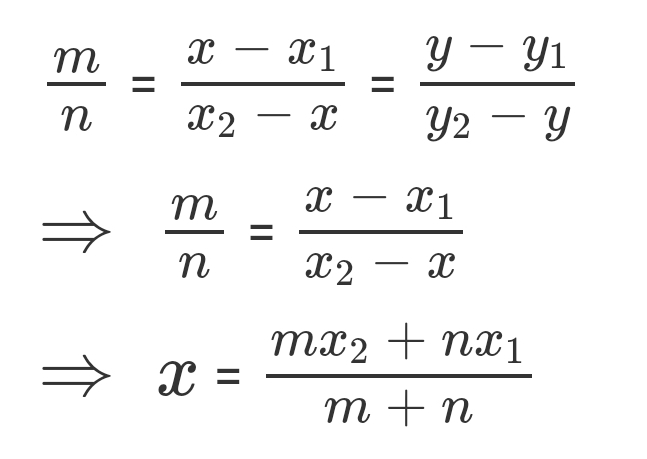
and

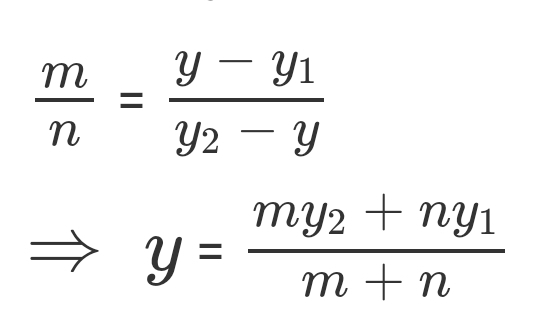
This leaves us with our original formula, meaning that the point M(x,y) joining the points P(x1,y1) and Q(x2,y2) internally with the ratio m:n has the coordiantes:

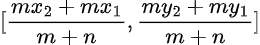
External Division

There is a variation of the formula for when the point is dividing the section is not within the line itself, this variation is useful to learn as it allows us to apply the formula in many scenarios without problem. The formula this time can be defined as:

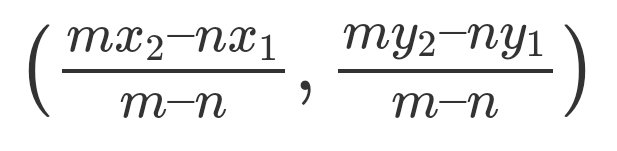
Derivation

We can prove this formula through the below example, for point A(x1, y1), C(x,y) is a point which divides our line OA by a ratio of 2:1 where O is the origin. This therefore means that OC:CA = 2:1

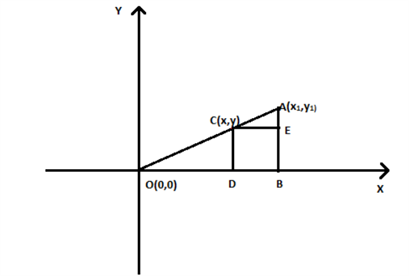
To help find the coordinates of C, lines are drawn to where CD and AB are perpendicular to the x-axis and CE is parallel to the x-axis.

∠COD is equal to ∠ACE through correspondence, they both equal to 90 degrees.
Much like the last derivation, the triangles ΔOCD and ΔCAE are around equivalent through Angle-Angle criterion of similarity.

This therefore implies that the ratio of the corresponding sides will be equal, for example:

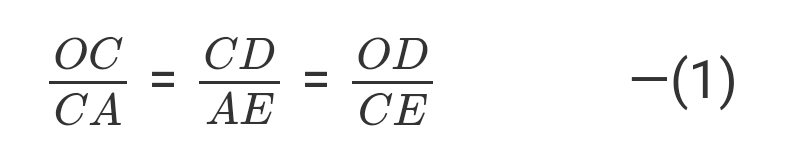
We know that the coordinates of C or x and y. This means that OD will be x and BE = CD = y

From this, CE = BD = OB - OD = (x1 - x)
AE = AB - BE = (y1 - y)
OC:CA = 2:1
CA = a, which is constant

From here we can form the equations:

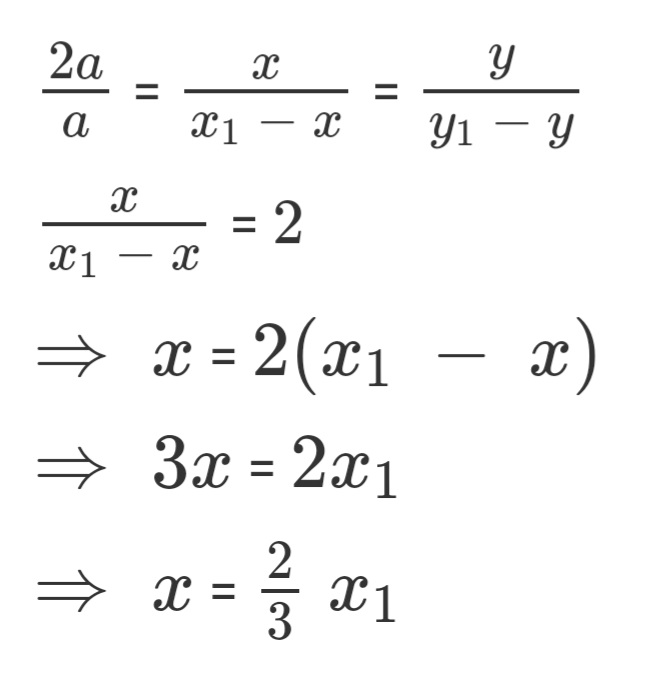
and

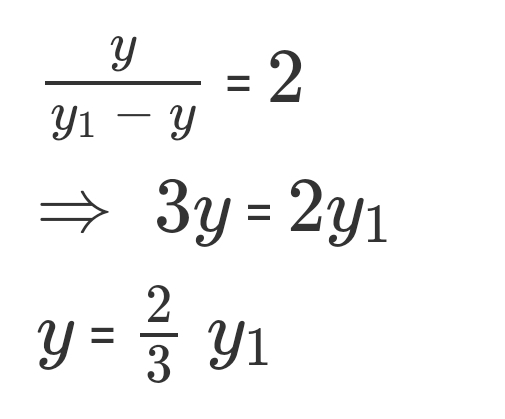
Finally, this leads us to deduct that the coordinates of point C are ((2/3)x1,(2/3)y1)

And giving us our equation:

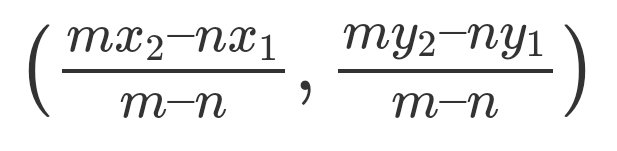
Midpoint Case

There is a special case for the sectional formula, where point M divides the line segment for points P(x1,y1) and Q(x2,y2) is the midpoint of the segment PQ.

If this is the case then we can say that the ratio m:n will be 1:1, meaning m,n both equal 1. This gives us the coordinates for the point M as: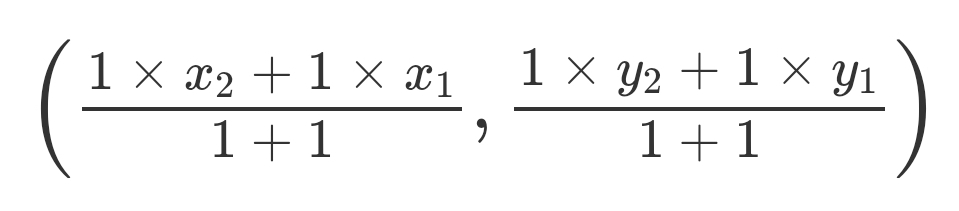

This derives the formula for a midpoint between two points as the above formula can be rearranged to:

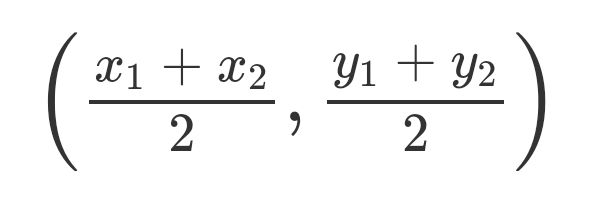
Implementation

Below is an implementation of the internal formula in Python:

def section_formula(x1, x2, y1, y2, m, n):
  
    x = (float)((n * x1)+(m * x2))/(m + n)
    y = (float)((n * y1)+(m * y2))/(m + n)

    print (x, y)
  
x1 = int(input("Enter x1 value: "))
x2 = int(input("Enter x2 value: "))
y1 = int(input("Enter y1 value: "))
y2 = int(input("Enter y2 value: "))
m = int(input("Enter M value: "))
n = int(input("Enter N value: "))
section_formula(x1, x2, y1, y2, m, n)

It is simple to understand, we just apply the formula we set out above and input the values for the points.

Overview

In this article at OpenGenus, we have covered the section formula and given two variations which can be applied either when a point is inside or outside of a line. For each formula, we have derived through triangles and the likes. We have also presented a special case in which the midpoint is found, and finally gave a Python implementation to further explain the idea.