In this article, we have explored the basic concepts of Trigonometry. These concepts are important for the Mathematics required for Computational Geometry.

Table of Contents

• Introduction
• Sine, Cosine, Tangent
• Cosecant, Secant, Cotangent
• Identities
• Addition/Subtraction Formulae
• Double-angle Formulae
• Overview

Introduction

In this article we will be covering the basis of trigonometry, this is the branch of mathematics concerning the relationship between sides and angles in triangles, and also the trigonometric functions which relate to circles. We will cover the main trigonometric functions and describe their characteristics as well as go over some useful identities and formulas that are essential in order to solve trigonometric problems.

Sine, Cosine, Tangent

The three main trigonometric functions are sine, cosine and tangent. We can use the functions to find angles within a triangle given sides, or to find sides given an angle and a side. The definitions of each function can be seen below:

As you can see we categorise the sides right-angled triangle and label them based on the angle we want to find, for example, if we were looking for angle CAB, and had the opposite and hypotenuse side, we would be able to use the sine function in order to find theta. Note that here, opposite is labeled as such to be opposite to the desired angle. A common acronym to remember this is SOH CAH TOA since it spells out the initials of the function and which sides needed clearly. To find sides given an angle, we shall use the inverse of these functions, or arc. This can be thought of as the angle whose function is _. For example the angle whose tan is 0.577 is π/6rad.

Each function can be represented as waves which will come in useful knowing later for translations (when working out solutions within a range) and for visualising where the different functions repeat in order to predict what kind of answers to expect.

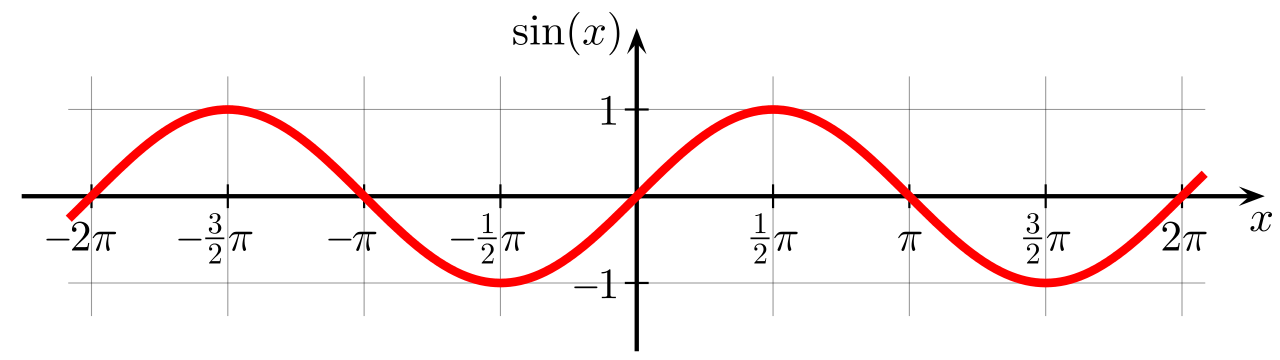
The sin function starts at 0, has a domain of all real numbers and a co-domain of [-1,1]. It repeats every 2π.

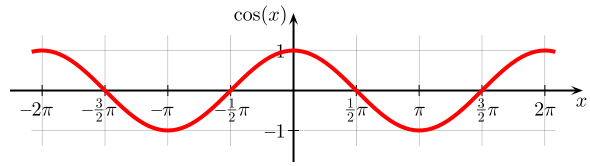
The cosine function is identical to the sine function having a domain of all real numbers and a co-domain of [-1, 1], repeating at 2π however starts at 1 instead of 0.

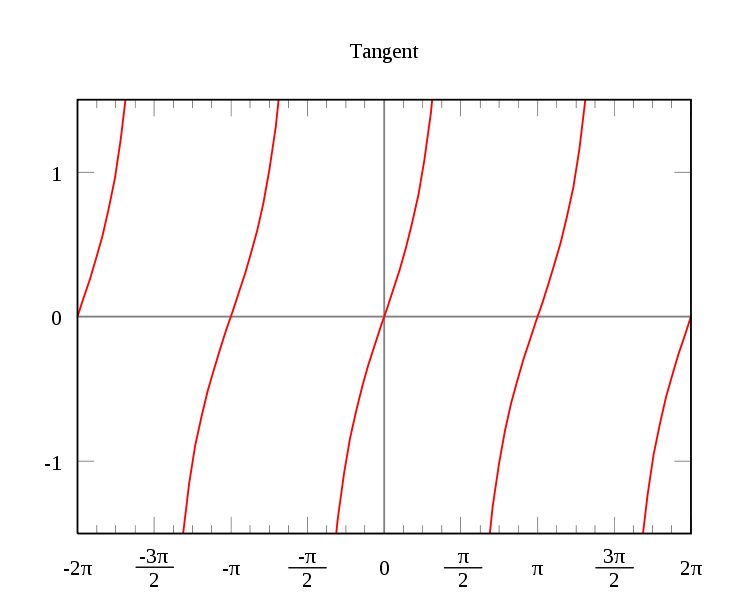
The tangent function is periodic function, repeating every π radians. Having a domain of all real numbers except where cos(x)=0, and a co-domain of the entire set of real numbers.

Cosecant, Secant, Cotangent

The cosecant, secant and cotangent functions (csc, sec, cot) are the reciprocals of the three functions we have talked about so far. For example, as tan would be defined as O/A, cot is defined as A/O. A good way to remember which of the three functions relate to which reciprocal function is to look at the third letter, in each case the third letter of the reciprocal is the starting letter of its function. Cosecant(Sine), Secant(Cosine) and Cotangent(Tangent).

We can see the graphs of these reciprocals have asymptotes where each function usually crosses the x-axis.

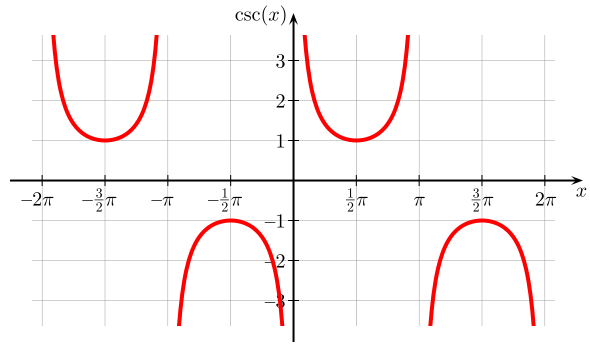
The cosecant function has a domain of all real numbers except where sin(x) = 0 and a co-domain of y <= -1 | y >= 1.

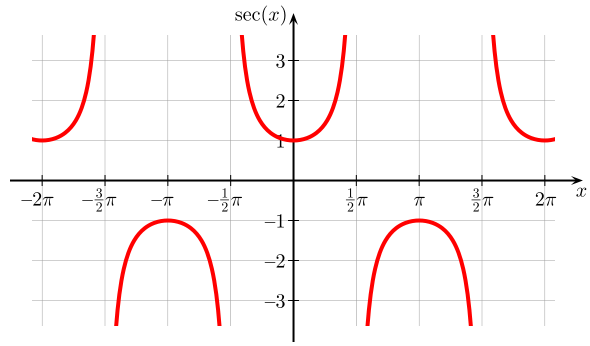
The secant function has a domain of all real numbers except where cos(x) = 0 and a co-domain of y <= -1 | y >= 1.

The tangent function has a domain of all real numbers except where sin(x) = 0 and a co-domain of all real numbers.

These 6 functions are not the only trig functions which exist however they are the most common ones and all we need for the purposes of this article. For example, we will cover the likes of hyperbolic functions at a later point which take area as an argument and are used for things such as architecture or the activation functions for neural networks.

Identities

There are common trigonometric identities that are extremely useful to know when dealing with such problems, these can be seen below:

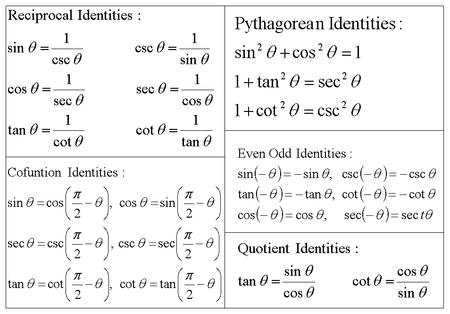
In addition to these identities, we shall also find identities for the values of each function given a commonly used angle. These can be seen below:

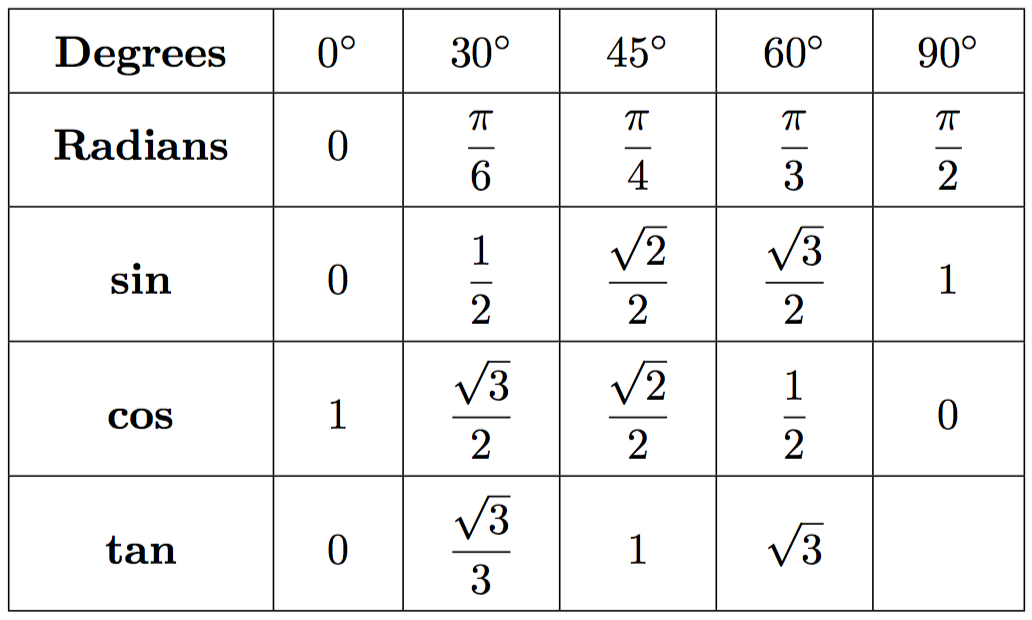
We can derive these angles using two triangles:

By working out the angles or sides using the relevant functions, we will be given these exact values. This is useful when dealing with trig as it speeds up the problem solving time rapidly if you learn what these common values are and don't have to calculate them yourself every time.

Additon and Subtraction Formulae

As well as identities there are a number of useful formulae to use when one has to deal with situations such as cos(a + b), below are useful ways that we can use formulae to manipulate the functions to become easier to deal with.

Double Angle Formulae

To supplement the previous formulae, we also have cases where the function will be presented for example as sin(2a). There are formulae we can use for this scenario called double-angle formulas. These can be seen below:

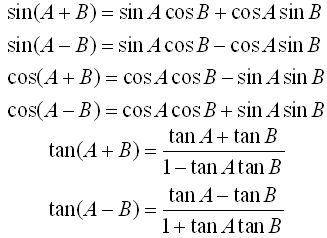
Overview

In this article at OpenGenus, we have covered the basis of trigonometry. We have included the basics of fundamental principles such as trigonometric functions, identities, formulae and described in which cases to apply them. After reading you should have a good understanding of the topic ready to apply to further problems in the future.