
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we have explored algorithm to find the Direction of point from line segment.
Table of Contents
- Introduction
- Method
- Example
- Implementation
- Overview
Introduction
In this article we will be covering how to calculate the direction of a point from a line segment. This means, if we have a point (P) and line (AB) we determine the direction of P from the line segment, whether it is to the left or to the right. This is a basic problem to solve which will eventually allow us to apply it to more complex problems such as segment intersection or calculating a convex hull.
Method
The problem is simple in nature, we will describe it below. In this problem, there can only be three possibilities for the point, to the left, to the right or directly on the given line segment. We will use cartesian planes as it is a 2D problem. We can solve this problem through using cross-product vectors.
If we have two point A and B, we know the cross-product of these two points is Ax * By - Ay * Bx. X and Y representing the coordinates of A and B respectively. A property of the cross-product is that the cross-product of points is positive only if the angle of the points at the origin is clockwise. From this, we can deduce that points on the right side of the line segment have a positive cross-product and points on the left side of the line have a negative cross-product. For this to be true we first need one of the points to be the origin, meaning that we shall also convert any three point system to be that one of the points is the origin for us to apply this cross-product property.
Example
To demonstrate our method and make it clearer to see what we mean, I shall provide an example which shows in why each case leads to the conclusion.
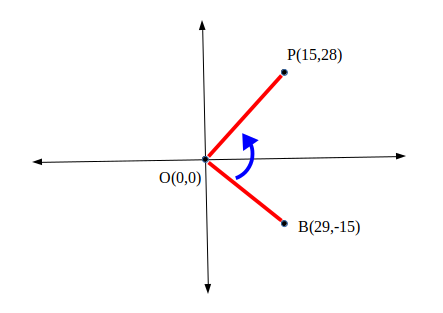
Take this diagram, angle BOP is in an anti-clockwise direction and has the cross product of BP. This equals 2829-15*(-15) = 1037, which is positive.
As it is clear from the image, a positive cross product will indicate the point to the right side of the line segment and if it was negative it will be to the left. As mentioned above, this assumes one of the three points will be the origin meaning that we shall manipulate the points to fit this assumption
Implementation
The following is an implementation of our algorithm in Python.
class point:
def __init__(self):
self.x = 0
self.y = 0
RIGHT = 1
LEFT = -1
ZERO = 0
def directionOfPoint(A, B, P):
global RIGHT, LEFT, ZERO
B.x -= A.x
B.y -= A.y
P.x -= A.x
P.y -= A.y
# Determining cross Product
cross_product = B.x * P.y - B.y * P.x
if (cross_product > 0):
return RIGHT
if (cross_product < 0):
return LEFT
return ZERO
if __name__=="__main__":
A = point()
B = point()
P = point()
A.x = int(input("Enter x coordinate of A: "))
A.y = int(input("Enter y coordinate of A: "))
B.x = int(input("Enter x coordinate of B: "))
B.y = int(input("Enter y coordinate of B: "))
P.x = int(input("Enter x coordinate of P: "))
P.y = int(input("Enter x coordinate of P: "))
direction = directionOfPoint(A, B, P)
if (direction == 1):
print("Right of line")
elif (direction == -1):
print("Left of line")
else:
print("On the line")
As you can see the process is fairly simple, we first make the origin as point A in order for our properties to be true, then, compute the cross-product of B and P (with A being the origin). Then, if the cross-product is greater than 0, return right, less than zero, return left and otherwise, it is on the line. After this, simply print to the console the direction of the point found.
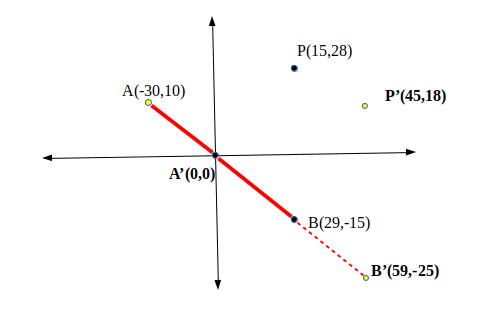
Take this example, our three points A, B, P shall be converted to A', B' and V' So that A is the origin, this can be seen in the code where we simply subtract A from the points P and B. After this we can then calculate the cross-product: 59*18-(-25)*18 = 2187 which is positive, so we can say that point P is on the right side of the line segment.
Overview
In this article at OpenGenus, we have described the process of calculating the direction of a point in relation to a line segment. We have solved this problem using cross-product vectors, if the cross product of the points is positive, the point is on the right side, negative is on the left and when it is 0 the point lies on the line segment. After explaining the process, we have also provided an implementation in code.
