In this article, we have explained how to check if line intersects circle and have provided three mathematical proofs along with implementation.

Table of Contents

• Introduction
• Algebraic Proof
• Geometric Proof
• Vector Proof
• Python Implementation
• Overview

Introduction

In this article we will explore the distance from a point to a line formula, it is a useful formula that can be used within coordinate geometry to check if a line intersects with a circle, hence making it a tangent. We shall derive the formula using various methods and then write code for it using an example problem.

The formula between the line ax + by + c = 0 and point (x0,y0) can be given as:

Where a, b, c are constant real numbers, representing the equation of the line, and a, b != 0.

This formula is finding the perpendicular distance between the centre of the circle and the line using the radius of the cirlce.

• If the distance is greater than the radius, then the line is outside the circle
• If the distance equals the radius, then the line is touching the circle
• If the distance is less than the radius, the line is intersecting the circle

We shall prove this formula below.

Algebraic Proof

We can derive this formula algebraically if the line is not horizontal or vertical, and a and b != 0.

We know that the line ax+by+c=0 has the gradient -a/b -> this means that a perpendicular line will have the gradient of b/a as it is the negative reciprocal.

If the point (n,m) is the point of intersection of our line that it passess through the point (x0,y0). This line through the point of intersection and the point we are checking will be perpendicular to the original line. This gives us:

We can represent the fact that (m,n) is on the line ax+by+c=0 as such by squaring:

Which implies that:

If we find the distance between the two points using distance formula, we get:

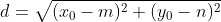
Finally we can rearrange this equation to get the original that we set out at the start of the article:

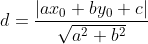
Geometric Proof

We can also prove this geometrically if, again, the line isn't horizontal or vertical.

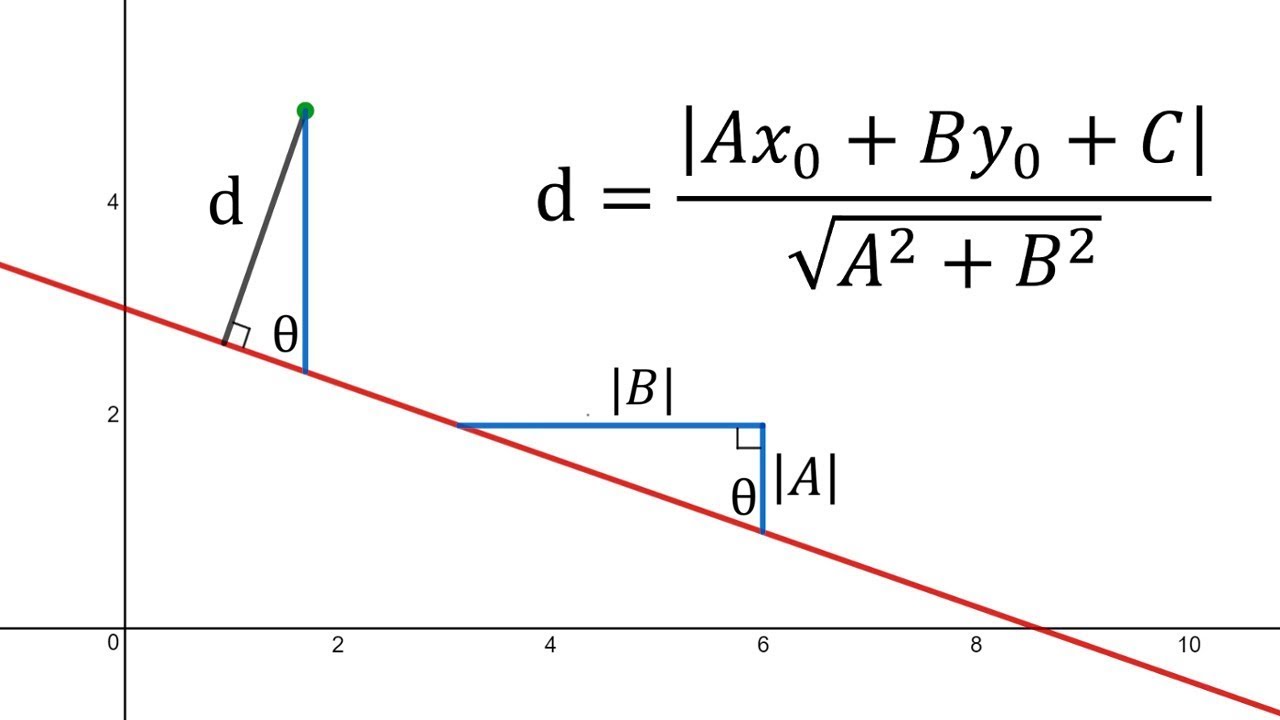
Let the red line be the line with the equation ax+by+c=0 and the point highlighted in green P, with the coordinates of (x0,y0).

We can drop a perpendicular to the line ax+by+c=0, labeled d from point P. Let the foot of this perpendicular be R. We can also draw a vertical line through point P (highlighted in blue) and label the point of intersection S.

At any point (T) on the line, we can draw a right angle triange TVU with horizontal and vertical line segments with the hypotenuse TU on a line and horizontal side of |B|. This means the vertical side of the traingel will have length |A| since the gradient of the line is -A/B.

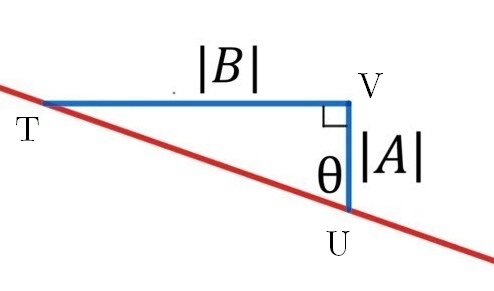
We have constructed two triangles PRS and TVU, they aer similar as they are both right angle triangles and ∠PSR approx. ∠TUV as they corresponding angles of a traversal of the parallel lines PS and UV. These sides of the triangle are in the same ratio, therefore we can deduce:

Let point S have the coordinates (x0,m) -> |PS| = |y0-m|. The distance from P to the line can be represented as:

We know that S is on the line, therefore we can find the value of m by:

Once we have m, this gives us the original equation of:

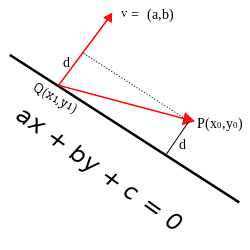
Vector Proof

Let P be the point with our coordinates (x0,y0) and the line equation as ax+by+c=0. We can also create another point Q, with the coordinates (x1,y1) which can be any point on the line and a vector v (a,b) which starts on point Q. Vector v is perpendicular to our line. The distance from P to Q is equal to the length of the orthagonal projection

on vector v.

We can write this projection length as:

We can find by subtracting points ->

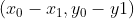
Using this, we can deduce: 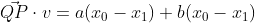and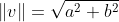

We know that Q is a point on the line so we can write c as -ax1 -by1. Finally from this we can get the original equation:

We can see a visual representation of this below.

Python Implementation

You can read the python implementation below:

import math

def check_intersection(a,b,c,x,y,rad):

    dist = ((abs(a*x+b*y+c))/math.sqrt(a**2+b**2))

    if (rad == dist):
        print("Touching")
    elif (rad > dist):
        print("Intersection")
    else:
        print("Lies outside")

rad = 10
a = 2
b = 3
c = 4
x = 5
y = 0
check_intersection(a,b,c,x,y,rad)

This algorithm is simple in design, first, we input values into the formula using math library, then use branching statements to determine whether the distance is greater, equal to or less than the radius. We then use this information to print what position the line is in relation to the point on the circle.

In our case: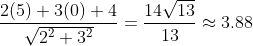

Using the values we input, the perpendicular distance was approximately 3.88, if we compare this to the radius of the circle which was 10, this is clearly smaller, therefore we can say that this line intersects with the circle.

Overview

In this article at OpenGenus, we have explained and derived the distance from a point to a line formula in various ways (from algebra, geometry and vectors) then described how to use it in the context of circles. We have also implemented this formula in python and gave an example problem, after reading this article, you should have a strong grasp of this formula and be able to use it for yourself and understand its principles.