In this article, we have covered Mathematics for Computational Geometry focused on 2D Shapes such as Circle properties/ theorems, Polygons and more.

Table of Contents

• Introduction
• Circle Theorems
• Polygons
• Overview

Introduction

In the last section, we covered the basics of geometry including points, lines, curves, and some information about 2D shapes like triangles and circles. In this article, we shall further expand on this, covering topics such as circle theorems, polygonal shapes and more.

Circle Theorems

To further the discussion about circles in geometry, here we shall look at circle theorems and their functions. We can use these common properties of circles on a Euclidean plane in order to retrieve much information and data about circles, as well as use it to solve problems later down the line.

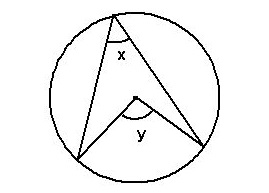
Angle at the centre is twice that of the circumference

The first theorem that we will look at states that the angle at the centre of the circle is double that of the angle at the circumference, this will be useful to us as it means with one of the two angles we are able to easily calculate the other.

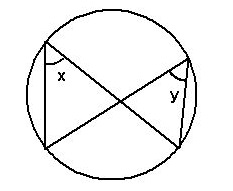
Angles within the same segment are equal

With this theorem, we can say that angles located in the same segment from a common chord will be equal. We can see this below:

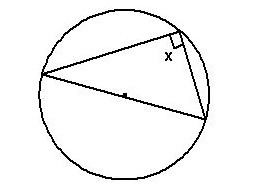
Angle in a semi-circle equals 90 degrees

This theorem means that if we have to find the angles within a semi circle, it will be formed from a right-angle triangle, and therefore an angle will equal 90 degrees.

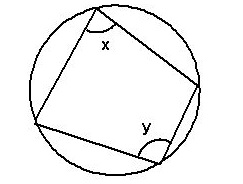
Opposite angles in a cyclic quadrilateral sum to 180 degrees

When we have a quadrilateral shape within a circle, the opposite angles will add to 180 degrees, this is because the interior angles of a quadrilateral add to make 360 degrees.

Perpendicular line from centre to chord will bisect the chord

This theorem states that if there is a perpendicular line to a chord, the chord will be bisected by that line.

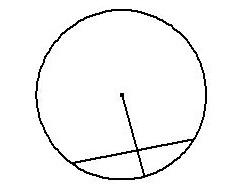
The angle between the radius and a tangent is 90 degrees

The next theorem states that the angle between the radius and a tangent to a circle will be 90 degrees. This is because any tangent is perpendicular to the radius of a circle at its point of contact.

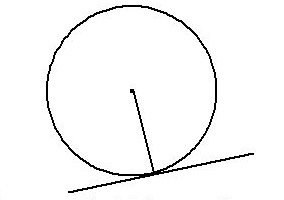
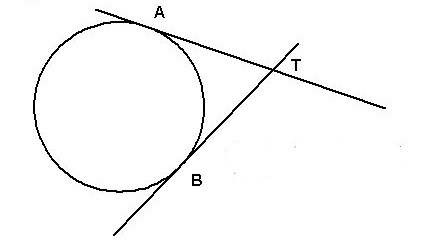
Tangents from a point outside the circle are equal in length

This theorem states that any tangents which stem from the same point outside of a circle will be equal in length.

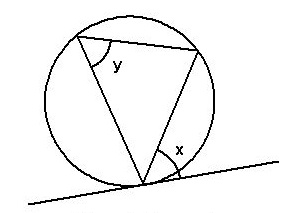
Angles in alternate segments are identical

The last theorem states that angles in alternate segments to each other are equal.

As you can see circle theorems are very useful during geometric calculations as they allow us to gain much more knowledge about a particular problem, when only having a small amount of info initially.

Polygonal Shapes

Polygonal shapes are closed, two-dimensional shapes which have straight line segments. They do not have any curved surfaces, they should have at least three sides. The line segments must intersect with each other only at their endpoints.

Polygonal properties

Polygons have properties which we can use to analyse them in problems, we will cover them below.

Regular polygons are that which all sides are equal in length and all internal angles are equal size. Irregular polygons therefore are all polygons which are not regular.

Concave polygons are polygons which have at least one internal angle greater than 180 degrees. Convex polygons are polygons which have no angles greater than 180 degrees. We can say that all regular polygons are also convex, but not all convex polygons are regular. Concave polygons are always irregular since not all of the internal angles can be equal however, not all irregular polygons are concave.

The third category we can place polygons in is simple or complex. Simple polygons are ones that have no intersecting sides. Complex polygons on the other hand are ones that have sides which intersect, this also means that regular facts about polygons may not apply.

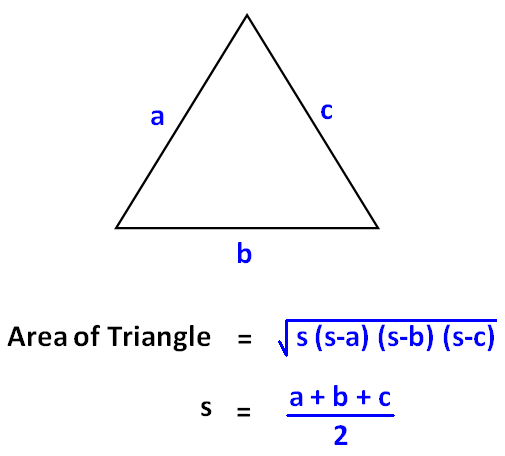
Heron's formula for area of a triangle

To further are explanation of polygons and to extend our analysis of triangles, there is a second formula to calculate area. This is called Heron's formula.

First, we calculate the perimeter by adding the three side lengths:
a + b + c = P

We then calculate S by dividing perimeter by 2:
S = P/2

Finally, we can use S in Heron's formula to get:
A = √S(S-a)(S-b)(S-c)

We will now also cover some useful equations for other polygons

Rectangles

There are three main formulas when it comes to rectangles, we will soon see how they become useful, especially when dealing with compound polygons where usually, we can split a shape into various sections to calculate things like area. Here, we write length and width as l and w respectively.

The area of a rectangle is simply:

a = l * w

The perimeter of a rectangle can be calculated using:

2l + 2w

Finally, we can write the diagonal of a rectangle as

√l^2+w^2

These three formulas are the basis of rectangle calculations, and can be used later on in various cases.

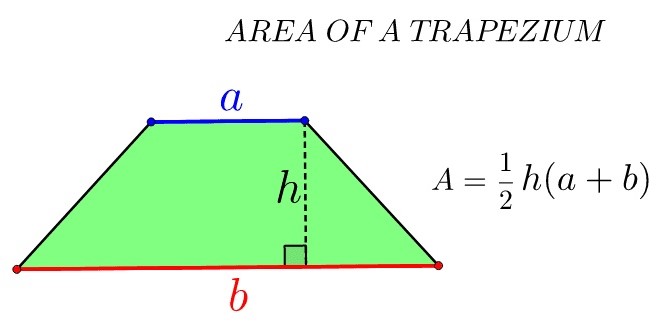
Trapezia

A trapezium is a quadrilateral shape with one pair of sides parallel to each other. We can find its area using this formula:

A = ((a+b)/2)*h

where a and b are side lengths and h is height

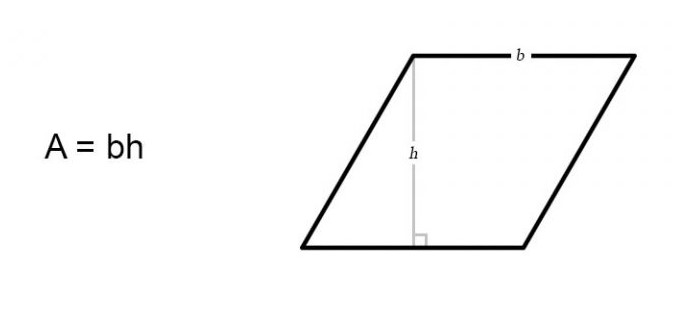
Parallelograms

Parallelograms are similar to trapezia however they have two pairs of parallel sides, the opposite sides are equal in length and the opposite angles are also equal. The area of this polygon can be found using:

A = b*h

where b is base and h is height

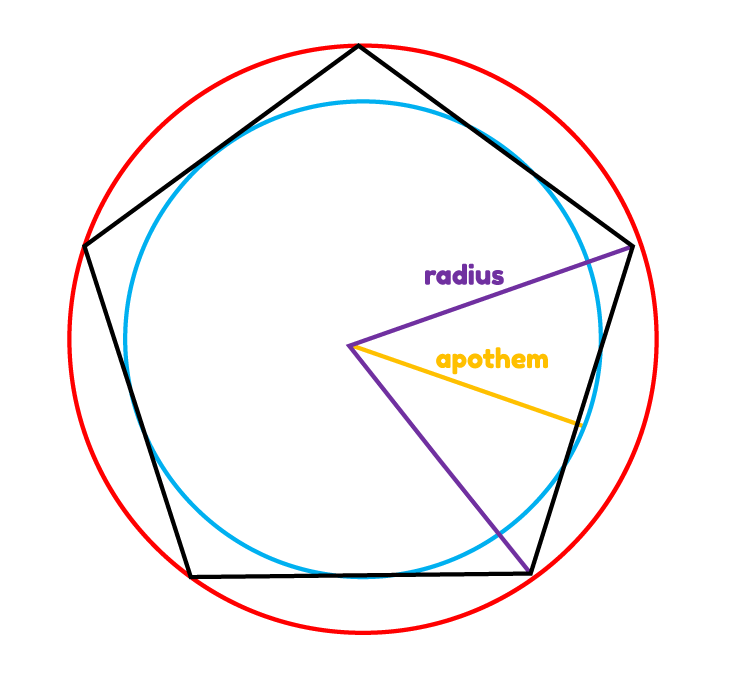
Pentagons

A 5 sided polygon is known as a pentagon. We can calculate its area using the apothem. This is a segment which spans from the centre to the midpoint of a particular side. Using this knowledge, we can calculate the area of a pentagon using the formula

A = 1/2*a*5(s)

where a is the apothem and s is the side length

If we do not have the length of the apothem, we can also use a formula which involves just the side length.

A = 1/4(√5(5+2√5)s^2

This way, we can calculate the area without having to know the apothem

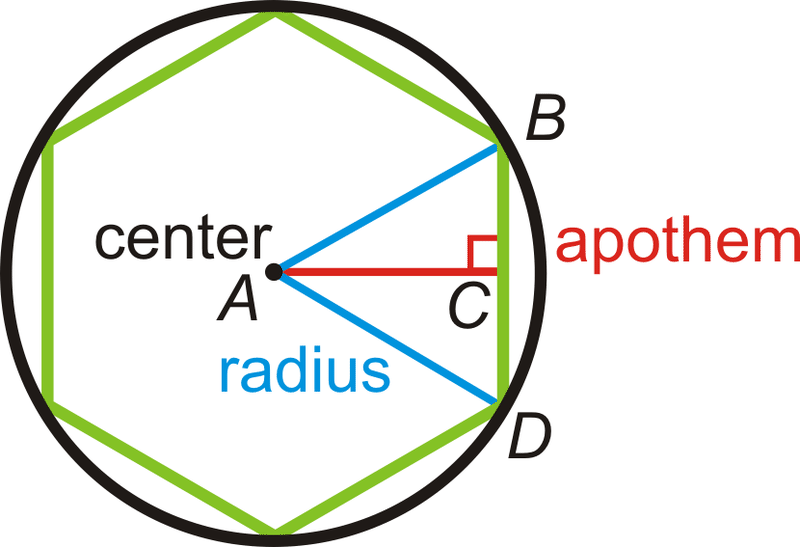
Hexagons

In a much similar way to a pentagon, we calculate the area of a hexagon using its apothem, using the formula:

1/2P*a

Where a is the apothem and P is the perimeter

Likewise, there is also an equation that exclusively uses side length, in case of the apothem or perimeter being unknown.

A = (3s^2√3)/2

Overview

We have delved further into geometric principles and presented numerous formulas for common shapes which will be useful to understand in the future. Additionally, in this article at OpenGenus, we have discussed properties of polygons and detailing circle theorems which will be convenient for us to use later on.