
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 20 minutes | Coding time: 5 minutes
A Graph is a finite collection of objects and relations existing between objects. If we represent objects as vertices(or nodes) and relations as edges then we can get following two types of graph:-
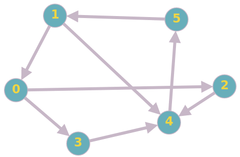
Directed Graphs: In directed graph, an edge is represented by an ordered pair of vertices (i,j) in which edge originates from vertex i and terminates on vertex j. Given below is an example of an directed graph.
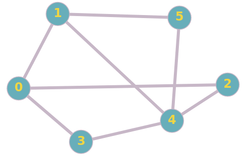
Undirected Graphs: In Undireced graph, edges are represented by unordered pair of vertices.Given below is an example of an undirected graph.
Representation
The two most common ways of representing graphs are:1. Adjacency matrix
2. Adjacency List
Adjacency Matrix
Let us consider a graph in which there are N vertices numbered from 0 to N-1 and E number of edges in the form (i,j). Where (i,j) represent an edge originating from ith vertex and terminating on jth vertex. Now, A Adjacency Matrix is a N*N binary matrix in which value of [i,j]th cell is 1 if there exists an edge originating from ith vertex and terminating to jth vertex, otherwise the value is 0. Given below are Adjacency matrices for both Directed and Undirected graph shown above:
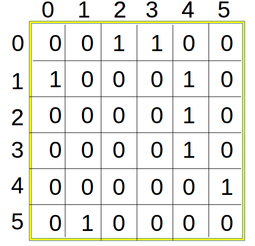
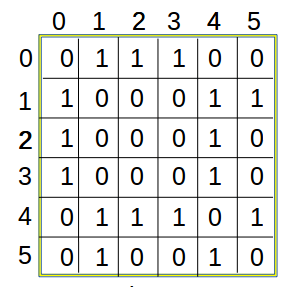
The pseudocode for constructing Adjacency Matrix is as follows:
Implementation1. Create a matrix A of size NxN and initialise it with zero.2. Iterate over each given edge of the form (u,v) and assign 1 to A[u][v]. Also, If graph is undirected then assign 1 to A[v][u].
/*
This code is for constructing adjacency matrix for undirected graph, with minor change it will also work for directed graph.
*/
#include <bits/stdc++.h>
using namespace std;
int main()
{
// where n is number of vertices and m is number of edges
int n, u, v, m;
cin>> n>> m;
int A[n][n];
for(int i=0; i<n; i++)
{
for(int j=0; i<n; j++)
A[i][j]=0;
}
for(int i=0; i< m; i++)
{
cin>> u>> v;
A[u][v]=1;
A[v][u]=1; // In case of directed graph this statement is removed.
}
// After above loop Adjcency matrix is ready.
for(int i=0; i<n; i++)
{
for(int j=0; j<n; j++)
cout<<A[i][j]<<" ";
cout << "\n";
}
return 0;
}
Adjacency List
Lets consider a graph in which there are N vertices numbered from 0 to N-1 and E number of edges in the form (i,j). Where (i,j) represent an edge from ith vertex to jth vertex. Now, Adjacency List is an array of seperate lists. Each element of array is a list of corresponding neighbour(or directly connected) vertices.In other words ith list of Adjacency List is a list of all those vertices which is directly connected to ith vertex. Given below are Adjacency lists for both Directed and Undirected graph shown above:
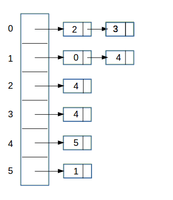
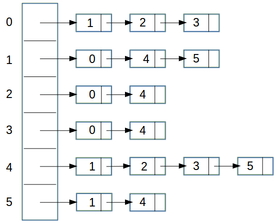
1. Create an array A of size N and type of array must be list of vertices. Intially each list is empty so each array element is initialise with empty list.2. Iterate each given edge of the form (u,v) and append v to the uth list of array A. Also, If graph is undirected append u to the vth list of array A.
Implementation
/*
This code is for constructing adjacency list for undirected graph, with minor change it will also work for directed graph.
*/
#include <bits/stdc++.h>
using namespace std;
int main()
{
// where n is number of vertices and m is number of edges
int n, u, v, m;
cin>> n>> m;
vector< vector<int> > A(n);
for(int i=0; i< m; i++)
{
cin>> u>> v;
A[u].push_back(v);
A[v].push_back(u); // In case of directed graph this statement is removed.
}
// After above loop Adjcency List is ready.
for(int i=0; i<n; i++)
{
cout<< i<< " ----> ";
for(int j=0; j<A[i].size(); j++)
cout<< A[i][j]<< " -->";
cout << "\n";
}
return 0;
}
Complexity
N denotes the number of nodes/ vertices and M denotes the number of edges
degree(V) denotes the number of edges from node V
Adjacency Matrix Complexity
Space: O(N * N)
Check if there is an edge between nodes U and V: O(1)
Find all edges from a node: O(N)
Adjacency List Complexity
Space: O(N + M)
Check if there is an edge between nodes U and V: O(degree(V))
Find all edges from a node V: O(degree(V))
Where to use?
As we have seen in complexity comparisions both representation have their pros and cons and implementation of both representation is simple. It is recommended that we should use Adjacency Matrix for representing Dense Graphs and Adjacency List for representing Sparse Graphs.
Note: Dense Graph are those which has large number of edges and sparse graphs are those which has small number of edges.
Application
-
Adjacency Matrix: Adjacency matrix is used where information about each and every possible edge is required for the proper working of an algorithm like :- Floyd-Warshall Algorithm where shortest path from each vertex to each every other vertex is calculated (if it exists). It can also be used in DFS (Depth First Search) and BFS (Breadth First Search) but list is more efficient there. Sometimes it is also used in network flows.
-
Adjacency List: Adjacency List is a space efficient method for graph representation and can replace adjacency matrix almost everywhere if algorithm doesn't require it explicitly. It is used in places like: BFS, DFS, Dijkstra's Algorithm etc.
