Maximise XOR of a given integer with a number from the given range

Given q queries each of specifies three integers x, l, r.  We have to find an integer from given range [l, r] inclusive, such that it gives maximum XOR with x. All values are assumed to be positive. We will show two ways to solve this interesting problem. One is the native approach which take O(R-L) time complexity and the other one is an efficient algorithm that takes only O(log X) time complexity.

Algorithm

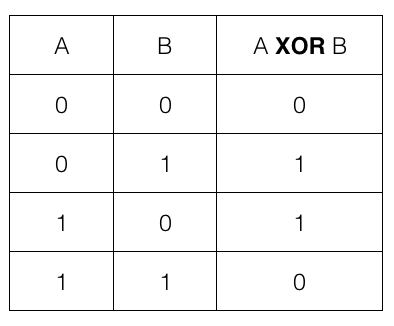
Naive Approach

One way to solve this problem is just to take XOR of each element in the range with x and the maximum result will be the answer. But if the range is too big this approach will take a lot of time.

Efficient Approach

Now, if we notice XOR is maximum when corresponding bits are NOT SAME. This is the idea we are going to use to solve this problem.

We will check each bit of integer x and decide whether to set corresponding bit in our answer or not. So, at every bit we have two choices to make:

1. We will want to set i ^th bit in our answer if this bit is reset in x. Now, the problem is we can overshoot our given range by setting i ^th bit or aur answer will be greater than r. So, we will set this bit if and only if setting this bit does not make our answer go beyond the given range.
2. The other and the remaining case is when i ^th bit is set in x. So, we will try to reset it in our answer to maximise XOR. Now, resetting the bit in our answer may make it lesser than given range value l. But there is a way we can reset this bit and still bring our answer in range. We will check whether summing up all the remaining bits with our answer will make it greater than or equal to l. If yes, we will keep this bit reset else we must set it.

Note: Since we have to Maximise XOR, we will always start from most significant bit (not the sign bit).

Approach is given below:

1. For ith bit in x, check whether it is set or reset.
2. Depending upon the bit, set or reset corresponding bit of the answer.
3. Check whether this answer is going beyond the given range or falling short.
4. If yes, flip this bit in the answer.
5. Repeat from step 1 till the last or 0th bit.

Pseudocode

The pseudocode of given problem is as follows:

1. For i:- 30 to 0:
2. Check the ith bit of x.
3. Try and set this bit in answer such that it doesnt go beyond range.
4. Else try resetting this bit such that it either stays in range or will be in range if rest of the bits are summed up.

Complexity

Time Complexity: O(log X) for integer X

Space Complexity: O(log X) for integer X

Implementation

   #include <iostream>
   using namespace std;

   int main()
   {
       int q;
       cin >>q;

       bool bits[31];
       while(q--)
       {
           int x, l, r;
           cin >>x >>l >>r;

           int temp = x;

           //storing bit values in boolean array
           for(int i = 0; i < 31 ;i++)
           {
               if(temp & 1) bits[i] = true;
               else bits[i] = false;

               temp = temp / 2;
           }

           for(int i = 30; i >= 0 ;i--)
           {
               //here (1 << i) is 2i
               temp = 1 << i;

               //if ith bit is set but resetting it in answer
               //will make our answer smaller than l
               if( bits[i] && (ans + temp - 1 ) < l )
                   ans += temp;

               //if ith bit is not set and setting it in answer
               //will not make our answer go beyond r
               else if( !bits[i] && (ans + temp) <= r )
                   ans += temp;
           }

           cout << (ans ^ x) <<"\n";
       }
   }
   

References

GitHub Link
Problem Link