
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 15 minutes | Coding time: 2 minutes
Bitwise operators are one of the most under-rated operators in C/C++, despite being quite fast as most of the processors today have direct support for bit level operators.
In this article, we will explore how to determine if a number is a power of 4 based on bitwise operations.
To pique your interest, we are going to suggest you to try solving a problem as efficiently as possible. So the problem goes as follows:
You need to check if a number is power of 2 or not.
An obvious and trivial solution which comes to mind is keep dividing the number by 2 until you cannot and check if the number is 1 or 0.
On thinking further, we see that we are taking O(log(n)) to solve such a simple problem.
Can this be improved?
Of course, and Bitwise operators come to our rescue. But before that we need to study simple property of binary number which are powers of 2.
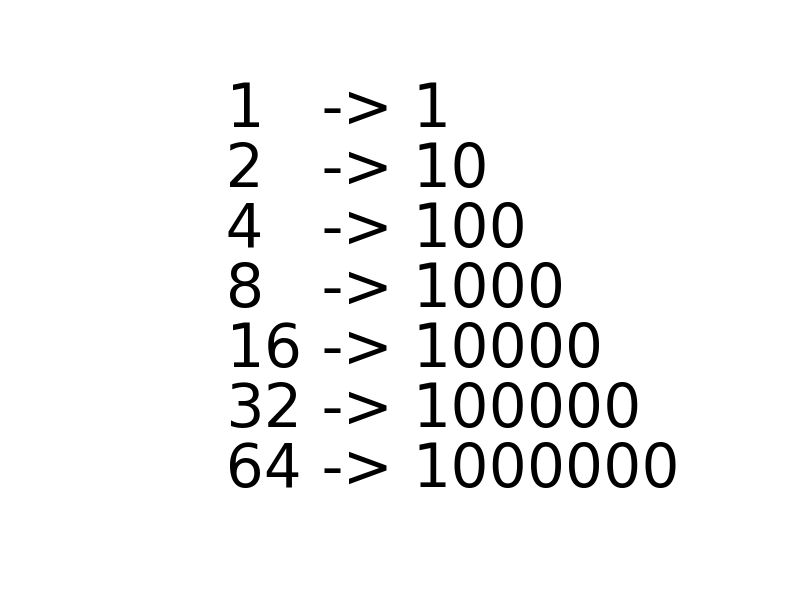
Can you see where we are going?
The powers of 2 have only one set bit in their Binary representation.
Let me be more explicit. If we subtract 1 from a power of 2 what we get is 1s till the last unset bit and if we apply Bitwise AND operator we should get only zeros.
This whole algorithm has a complexity of O(1).
We can prove the correctness of algorithm.
Suppose if there is a 1 to the left of first set bit, i.e., it is not a power of 2. We can clearly see that n & (n - 1) will not return 0.
| 16 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
|---|---|---|---|---|---|---|---|---|
| 16-1=15 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 16 AND 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Hence, 16 is a power of 2.
| 15 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
|---|---|---|---|---|---|---|---|---|
| 15-1=14 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 15 AND 14 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
Hence, 15 is not a power of 2.
Algorithm
Why all this drama for power of 4?
Well to check if a number is power of 4 we will need to check first if there is only one set bit in the binary representation of the number and that there are even number of zeros to the right of the set bit.
| 16 | : | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
|---|
There are 4 (even) zeros after set bit, hence, 16 is a power of 4.
| 32 | : | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
|---|
There are 5 (not even) zeros after set bit, hence, 32 is not a power of 4.
Implementation
- C
- C++
C
#include <iostream>
// Function to check if the number "x" is power of 4
bool is_power_of_4(int x)
{
// Binary represntation of 3 -> "11"
int chkbit = 3;
// Check if the number has only one set bit
if ((x & (x - 1)) != 0)
return false;
// Left-shift the number by 2 bits and check
// if last two bits are zeros.
while ((chkbit & x) == 0)
x >>= 2;
// Return true iff the last bit is set.
return ((x & chkbit) == 1);
}
int main(int argc, char *argv[])
{
int n;
std::cout << "Enter a number:" << std::endl;
std::cin >> n;
// Print the result
std::cout << ((is_power_of_4(n)) ? "YES" : "NO") << std::endl;
return 0;
}
Complexity
- Worst case time complexity:
Θ(log N) - Average case time complexity:
Θ(log N) - Best case time complexity:
Θ(1) - Space complexity:
Θ(1)
