
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 25 minutes | Coding time: 10 minutes
Ever since the idea of artificial intelligence dawned upon the humanity, the basic concept of playing games against an unbeatable opponent, and that too.. AI has came out to be an exciting prospect. The first chess programs were written by Claude Shannon and by Alan Turing in 1950, almost as soon as the computers became programmable.
In this article, I will be demonstrating the power of Minimax theorem as applied to Tic-Tac-Toe. But before that, allow me to introduce you to Minimax.
Minimax is a recursive algorithm which is used to choose an optimal move for a player assuming that the other player is also playing optimally. It is used in games such as tic-tac-toe, go, chess, isola, checkers, and many other two-player games. Such games are called games of perfect information because it is possible to see all the possible moves of a particular game. There can be two-player games which are not of perfect information such as Scrabble because the opponent's move cannot be predicted.
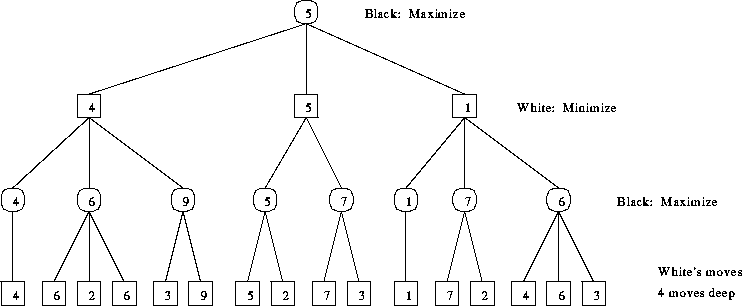
It is pretty much synonymous to our thought process when we play a game and ask ourselves the limits of our opponent's move when we make this move!
Fun fact : Minimax is called so because it helps in minimizing the loss when the opponent choses the strategy inflicting maximum loss to us! Minimax, indeed !
Minimax in Tic-tac-toe
For understanding an intriguingly beautiful algorithm like minimax , we require an equally fun medium of portrayal of idea, and nothing can beat a simplisticly easy game of tic-tac-toe!
To begin, let's start by defining what it means to play a perfect game of tic tac toe:
If I play perfectly, every time I play I will either win the game, or I will draw the game. Furthermore if I play against another perfect player, I will always draw the game.
How might we describe these situations quantitatively? Let's assign a score to the "end game conditions:"
- I win? I get 10 points!
- I lose? I lose 10 points (because the other player gets 10 points)
- I draw? I get zero points, nobody gets any points at all!
The key to the Minimax algorithm is a back and forth between the two players, where the player whose "turn it is" desires to pick the move with the maximum score. In turn, the scores for each of the available moves are determined by the opposing player deciding which of its available moves has the minimum score. And the scores for the opposing players moves are again determined by the turn-taking player trying to maximize its score and so on all the way down the move tree to an end state.
A description for the algorithm, assuming X is the "turn taking player," would look something like:
- If the game is over, return the score from X's perspective.
- Otherwise get a list of new game states for every possible move
- Create a scores list
- For each of these states add the minimax result of that state to the scores list
- If it's X's turn, return the maximum score from the scores list
- If it's O's turn, return the minimum score from the scores list
You'll notice that this algorithm is recursive, it flips back and forth between the players until a final score is found.
A sample run of the game is given below :
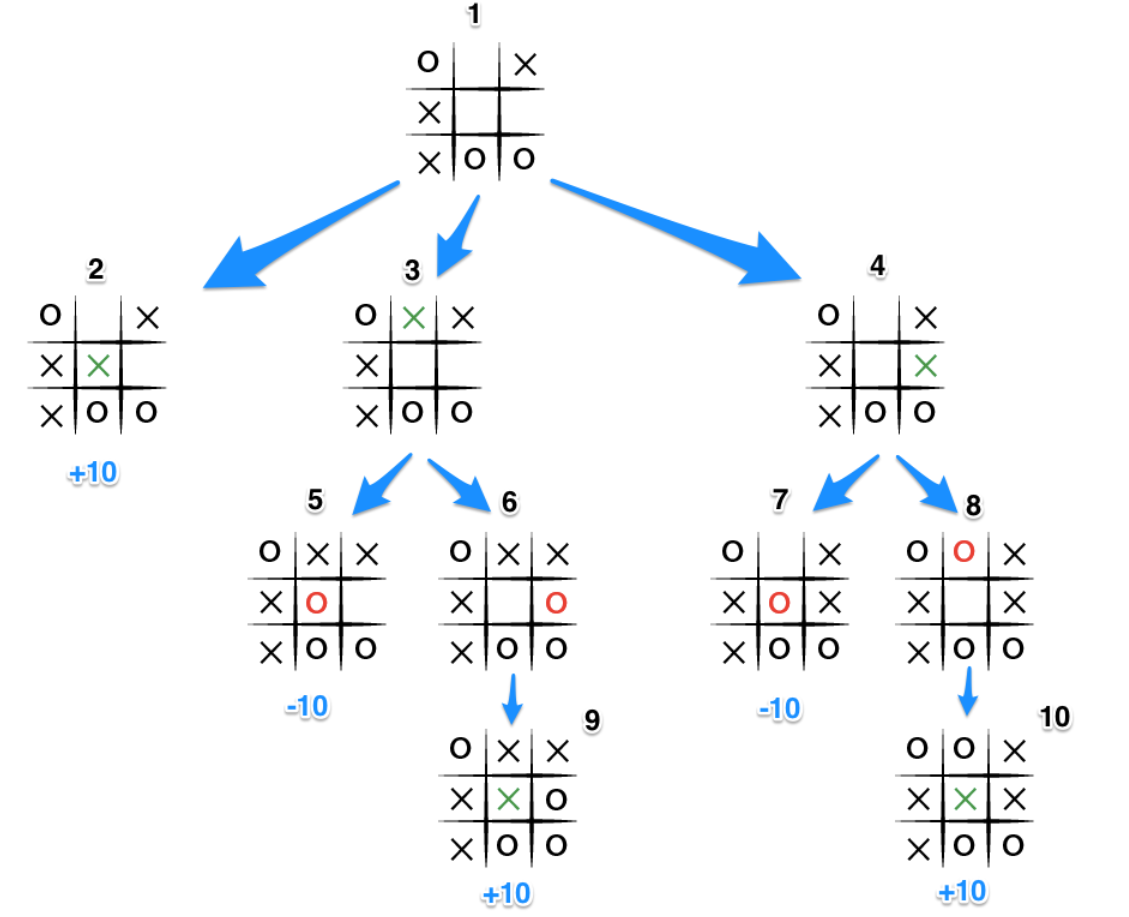
But, there is one flaw in the algorithm, it doesn't respect the matter of making the move immediately. It does know that X may ultimately lose or win in the situation, but doesn't always make the correct move to maximise the score. So, how do we fix that?
- The Answer : Depth
The key improvement to this algorithm, such that, no matter the board arrangement, the perfect player will play perfectly unto its demise, is to take the "depth" or number of turns till the end of the game into account. Basically the perfect player should play perfectly, but prolong the game as much as possible.
In order to achieve this we will subtract the depth, that is the number of turns, or recursions, from the end game score, the more turns the lower the score, the fewer turns the higher the score.
This is how the game flow looks like now :
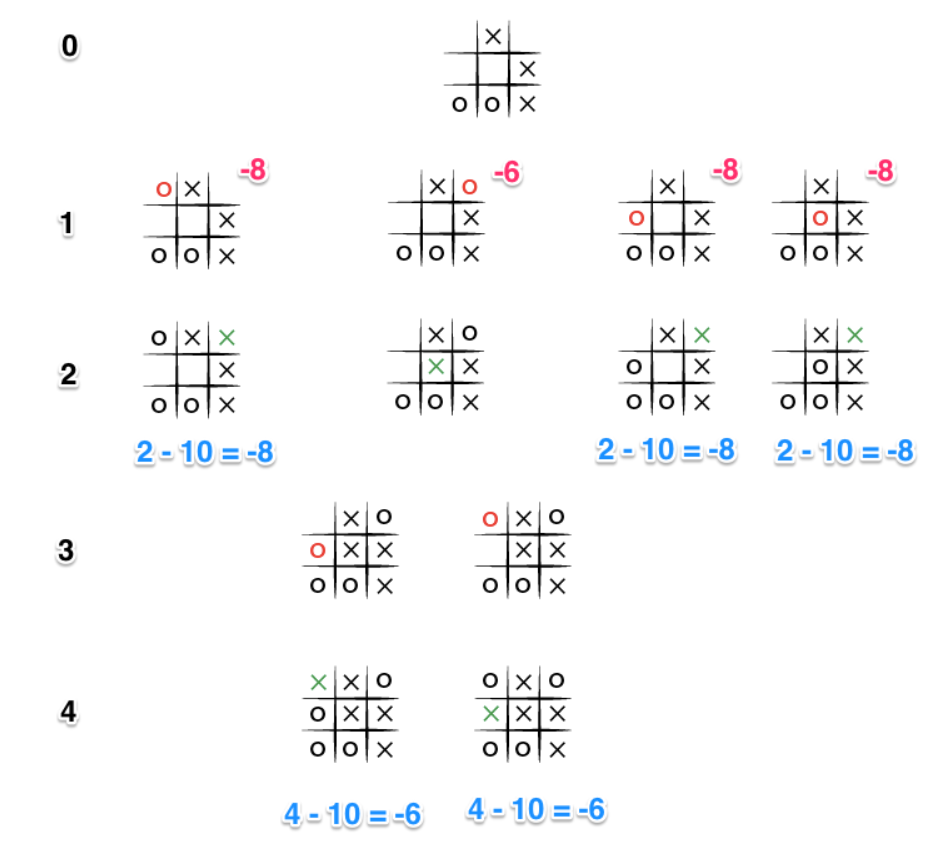
Algorithm
def scoring (game, depth):
@player
if game.win:
return 10 - depth
@opponent
else if game.win :
return depth - 10
else :
return 0
# end of function scoring
def minimax(game, depth)
if end_game :
return score(game)
depth += 1
scores = [] # an array of scores
moves = [] # an array of moves
# Populate the scores array, recursing as needed
game.get_available_moves.each do |move|
possible_game = game.get_new_state(move)
scores.push minimax(possible_game, depth)
moves.push move
end
# Do the min or the max calculation
if game.active_turn == @player
# This is the max calculation
max_score_index = scores.each_with_index.max[1]
@choice = moves[max_score_index]
return scores[max_score_index]
else
# This is the min calculation
min_score_index = scores.each_with_index.min[1]
@choice = moves[min_score_index]
return scores[min_score_index]
end
end
Complexity
- Worst case Performance :
O(|E|) = O(b^d) - Worst case space complexity :
O(|V|) = O(b * d)
Implementations
- Next Best Move Guesser- Python
Next Best Move Guesser- Python
from __future__ import print_function
class move:
def __init__(self,row,col):
self.row=row
self.col=col
human,pc='o','x'
board=[]
def isMovesLeft():
for i in range(3):
for j in range(3):
if (board[i][j]=='_'):
return True
return False
def evaluate(b):
for row in range(3):
if (b[row][0]==b[row][1] and b[row][1]==b[row][2]):
if (b[row][0]==pc):
return +10
elif (b[row][0]==human):
return -b10
for col in range(3):
if (b[0][col]==b[1][col] and b[1][col]==b[2][col]):
if (b[0][col]==pc):
return +10
elif (b[0][col]==human):
return -10
if (b[0][0]==b[1][1] and b[1][1]==b[2][2]):
if (b[0][0]==pc):
return 10
elif (b[0][0]==human):
return -10
if (b[0][2]==b[1][1] and b[1][1]==b[2][0]):
if (b[0][2]==pc):
return 10
elif (b[0][2]==human):
return -10
# Else if none of them have won then return 0
return 0;
def minimax(depth=1,chance=human): #initial after x places then chance of o goes
score=evaluate(board)
if (score == 10) or (score == -10):
return score-depth
if(isMovesLeft()==False): #draw
return 0-depth
if(chance is pc):
bestpc=-1000
for i in range(3):
for j in range(3):
if board[i][j] is '_':
board[i][j]=pc
bestpc=max(bestpc,minimax(depth+1,human))
board[i][j]="_"
return bestpc
else:
besth=1000
for i in range(3):
for j in range(3):
if board[i][j] is '_':
board[i][j]=human
besth=min(besth,minimax(depth+1,pc))
board[i][j]="_"
return besth
def findBestMove(board):
best=-1000
bmove=move(-1,-1)
for i in range(3):
for j in range(3):
if board[i][j] is "_":
board[i][j]=pc
temp=minimax()
board[i][j]="_"
if temp>best:
bmove.row,bmove.col=i,j
best=temp
print ('best',best,sep=' ')
return bmove
def main():
board.append(['x','x','o'])
board.append(['o','_','_'])
board.append(['x','_','o'])
bestmove=findBestMove(board)
print (bestmove.row,bestmove.col,sep=' ')
board[bestmove.row][bestmove.col] = pc
if __name__=="__main__":
main()
Applications
Minimax (now and again MinMax or MM) is a choice administer utilized as a part of choice theory, game theory, insights and reasoning for limiting the conceivable damage for a most pessimistic scenario (misere gameplay) situation. When managing picks up, it is alluded to as "maximin"— to augment the base pick up.
Initially defined for two-player zero-total game theory, covering both the situations where players take exchange moves and those where they make concurrent moves, it has likewise been reached out to more perplexing games and to general basic leadership within the sight of vulnerability.
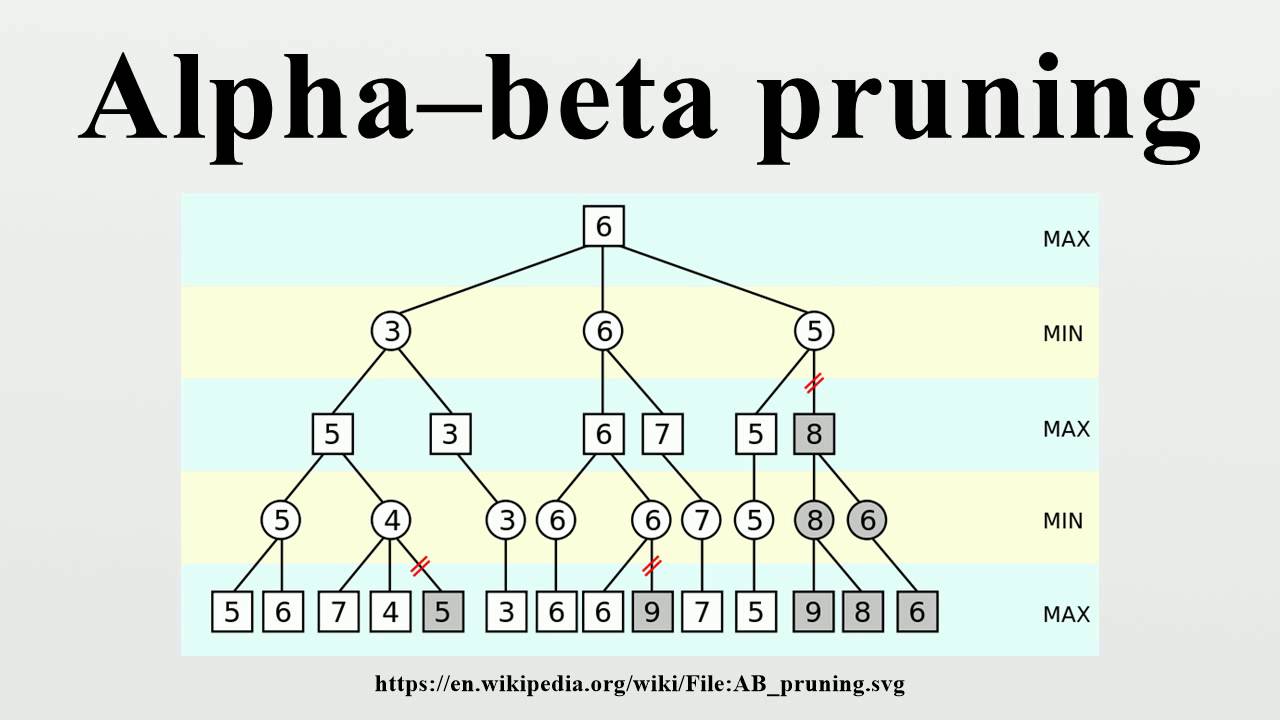
It can be further optimized with alpha-beta pruning and hash maps but those are for future references!
Questions
Which is the element which makes our minimax program smarter in tic-tac-toe?
Which is an optimising utlility in this Minimax theorem?
Further Reading
-
Coin Cidence Equality using Minimax: Research Paper by Xie Pin Ding
-
Minimax application in differential equations by CBMS
