Zobrist Hashing

Reading time: 15 minutes | Coding time: 5 minutes

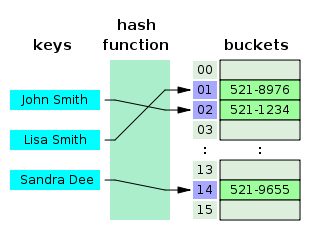
Zobrist hashing (additionally alluded to as Zobrist keys or Zobrist marks ) is a hash function development utilized as a part of computer programs that play unique board games, for example, chess and Go, to execute transposition tables, an exceptional sort of hash table that is listed by a board position and used to abstain from examining a similar position more than once. Zobrist hashing is named for its creator, Albert Lindsey Zobrist.

The idea behind Zobrist Hashing is that for a given board state, if there is a piece on a given cell, we use the random number of that piece from the corresponding cell in the table.

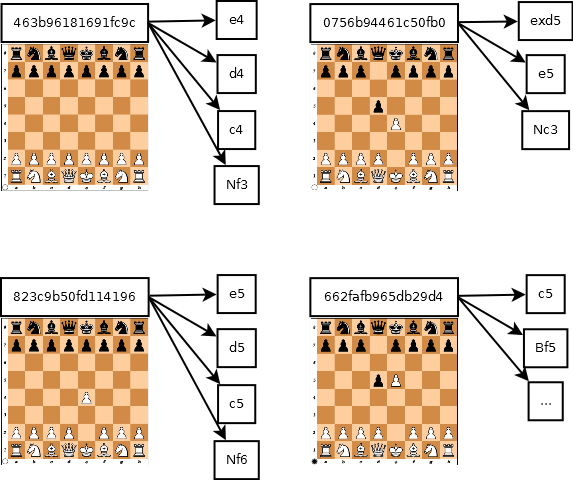
If more bits are there in the random number the lesser chance of a hash collision. Therefore 64 bit numbers are commonly used as the standard and it is highly unlikely for a hash collision to occur with such large numbers. The table has to be initialized only once during the programs execution.

Also the reason why Zobrist Hashing is widely used in board games is because when a player makes a move, it is not necessary to recalculate the hash value from scratch. Due to the nature of XOR operation we can simply use few XOR operations to recalculate the hash value.

Algorithm

Note :

• We don't really need Zobrist hashing in the game of tic-tac toe , alpha beta pruning does optimisation fine for that game.
• You won't be encountering this algorithm until and unless you are facing a really large board. Some thing like 8x8 (chess) or 16x16 (ultimate tic-tac-toe)

A matrix intialised with random numbers in the beginning
Table[number_of_board_cells][number_of_pieces]

def zobristHash(board):
    ''' returns hash according to current board config'''
    hash = 0
    for each cell on board : 
        if cell is not empty:
            piece = board[cell]
            hash ^= table[cell][piece]
    return hash

Complexity

• Worst case Performance : O(N)
• Worst case space complexity : O(|V|) = O(b * d)

Implementations

Hash Mapping in chess-Python

Hash Mapping in tic tac toe-Python

import random
zobTable = [[[random.randint(1,2**64 - 1) for i in range(12)]for j in range(8)]for k in range(8)]


'''for i in zobTable:
    for j in i:
        for k in j:
            print k,
        print 

'''

def indexing(piece):
    ''' mapping each piece to a particular number'''
    if (piece=='P'):
        return 0
    if (piece=='N'):
        return 1
    if (piece=='B'):
        return 2
    if (piece=='R'):
        return 3
    if (piece=='Q'):
        return 4
    if (piece=='K'):
        return 5
    if (piece=='p'):
        return 6
    if (piece=='n'):
        return 7
    if (piece=='b'):
        return 8
    if (piece=='r'):
        return 9
    if (piece=='q'):
        return 10
    if (piece=='k'):
        return 11
    else:
        return -1

def computeHash(board):
    h = 0
    for i in range(8):
        for j in range(8):
           # print board[i][j]
            if board[i][j] != '-':
                piece = indexing(board[i][j])
                h ^= zobTable[i][j][piece]
    return h
def main():
    # Upper Case are white pieces
    # Lower Case are black pieces

    # a [8][8] format board
    board = [
        ['-', '-', '-', 'K', '-', '-', '-', '-'],
        ['-', 'R', '-', '-', '-', '-', 'Q', '-'],
        ['-', '-', '-', '-', '-', '-', '-', '-'],
        ['-', 'P', '-', '-', '-', '-', 'p', '-'],
        ['-', '-', '-', '-', '-', 'p', '-', '-'],
        ['-', '-', '-', '-', '-', '-', '-', '-'],
        ['p', '-', '-', '-', 'b', '-', '-', 'q'],
        ['-', '-', '-', '-', 'n', '-', '-', 'k']
    ]

    hashValue = computeHash(board)
    print "Current Board is :"
    for i in board:
        for j in i:
            print j,
        print

    print "\nThe Current hash is : ",hashValue,"\n"

    # an exaple of channge in game state and how it affects the hashes

    # move white Rook to at a new postion in right
    piece = board[1][1]

    board[1][1] = '-'
    hashValue ^= zobTable[1][1][indexing(piece)]

    board[3][1] = piece
    hashValue ^= zobTable[3][1][indexing(piece)]
    print "The new board is :"
    for i in board:
        for j in i:
            print j,
        print

    print "\nHash after the move is : ",hashValue,"\n"

if __name__ == "__main__":
    main()

Python

import random
zobTable = [[[random.randint(1,2**10 - 1) for i in range(2)]for j in range(3)]for k in range(3)]

def indexing(piece):
    ''' mapping X and O to a particular number'''
    if (piece=='X'):
        return 0
    if (piece=='O'):
        return 1
    else:
        return -1
def computeHash(board):
    h = 0
    for i in range(3):
        for j in range(3):
            if board[i][j] != '-':
                piece = indexing(board[i][j])
                h ^= zobTable[i][j][piece]
    return h

def main():
    # X is player one and O is player 2
    # a [3][3] format board
    board = [
        ['-', 'O', 'X'],
        ['-', 'X', '-'],
        ['O', '-', 'O'],
    ]

    hashValue = computeHash(board)
    print "Current Board is :"
    for i in board:
        for j in i:
            print j,
        print

    print "\nThe Current hash is : ",hashValue,"\n"

    # an exaple of channge in game state and how it affects the hashes

    # Add X at [2][1] to disrupt the O's winning strategy

    piece = 'X'

    board[2][1] = piece
    hashValue ^= zobTable[2][1][indexing(piece)]
    print "The new board is :"
    for i in board:
        for j in i:
            print j,
        print

    print "\nHash after the move is : ",hashValue,"\n"

if __name__ == "__main__":
    main()

Applications

As it is evident, it is a major feature used in two player games like chess and go. Just like standard hashes , it can be a great tool for graph traversals along with insertion and deletion.

The same method has been used to recognize substitutional alloy configurations during Monte Carlo simulations in order to prevent wasting computational effort on states that have already been calculated !

Further Reading

• Zobrist Hashing for parallel-first best searches by AAAI Publications