
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time:
Like we discussed in earlier article, a hard coded AI can be used to create an intelligent opponent which you can challenge to a game of classical tic-tac-toe!
But, that algorithm could still be optimised further. But how do we achieve that? The Alpha Beta Pruning is a search algorithm that tries to diminish the quantity of hubs that are assessed by the minimax algorithm in its search tree. It is an antagonistic search algorithm utilized usually for machine playing of two-player recreations (Tic-tac-toe, Chess, Go, and so forth.).
It stops totally assessing a move when no less than one probability has been observed that ends up being more regrettable than a formerly analyzed move. Such moves require not be assessed further. At the point when connected to a standard minimax tree, it restores an indistinguishable move from minimax would, however prunes away branches that can't in any way, shape or form impact an official conclusion!
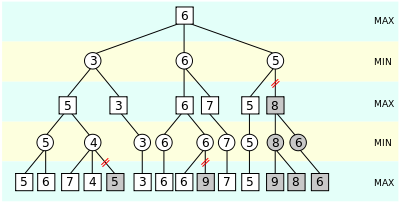
You must be thinking what does this figure really signifies. Well, it shows how the alogorithm ignores the sub trees which are not really desireable in our game moves. The algorithm keeps up two qualities, alpha and beta, which speak to the base score that the expanding player is guaranteed of and the greatest score that the limiting player is guaranteed of separately. At first alpha is negative infinity and beta is sure infinity, i.e. the two players begin with their most exceedingly terrible conceivable score. At whatever point the most extreme score that the limiting player(beta) is guaranteed of turns out to be not as much as the base score that the expanding player(alpha) is guaranteed of (i.e. beta <= alpha), the augmenting player require not consider the relatives of this hub as they will never be come to in genuine play.
Algorithm
Note :
-
Alpha Beta Pruning is not a new algorithm but actually an optimization!
-
Alpha is the best value that the maximizer currently can guarantee at that level or above.
-
Beta is the best value that the minimizer currently can guarantee at that level or above.
And ofcourse, we are using Tic Tac Toe as our reference example!
def minimax(depth, player, alpha, beta)
if gameover or depth == 0
return calculated_score
end
children = all legal moves for player
if player is AI (maximizing player)
for each child
score = minimax(depth - 1, opponent, alpha, beta)
if (score > alpha)
alpha = score
end
if alpha >= beta
break
end
return alpha
end
else #player is minimizing player
best_score = +infinity
for each child
score = minimax(depth - 1, player, alpha, beta)
if (score < beta)
beta = score
end
if alpha >= beta
break
end
return beta
end
end
end
#then you would call it like
minimax(2, computer, -inf, +inf)
Complexity
- Worst case Performance :
O(|E|) = O(b^(d/2)) - Worst case space complexity :
O(|V|) = O(b * d)
Implementations
- Next Best Move Guesser- Python
Interactive console game- Python
import numpy as np
import sys
from copy import copy
rows = 3
cols = 3
board = np.zeros((rows,cols))
inf = float("inf")
neg_inf = float("-inf")
def printBoard():
for i in range(rows):
for j in range(cols):
if board[i, j] == 0:
sys.stdout.write(' _ ')
elif board[i, j] == 1:
sys.stdout.write(' X ')
else:
sys.stdout.write(' O ')
print ''
# The heuristic function which will be evaluating board's position for each of the winning POS
heuristicTable = np.zeros((rows+1, cols+1))
numberOfWinningPositions = rows + cols + 2
for index in range(rows+1):
heuristicTable[index, 0] = 10**index
heuristicTable[0, index] =-10**index
winningArray = np.array([[0, 1, 2], [3, 4, 5], [6, 7, 8], [0, 3, 6], [1, 4, 7], [2, 5, 8], [0, 4, 8], [2, 4, 6]])
def utilityOfState(state):
stateCopy = copy(state.ravel())
heuristic = 0
for i in range(numberOfWinningPositions):
maxp = 0
minp = 0
for j in range(rows):
if stateCopy[winningArray[i,j]] == 2:
maxp += 1
elif stateCopy[winningArray[i,j]] == 1:
minp += 1
heuristic += heuristicTable[maxp][minp]
return heuristic
def minimax(state,alpha,beta,maximizing,depth,maxp,minp):
if depth==0:
return utilityOfState(state),state
rowsLeft,columnsLeft=np.where(state==0)
returnState=copy(state)
if rowsLeft.shape[0]==0:
return utilityOfState(state),returnState
if maximizing==True:
utility=neg_inf
for i in range(0,rowsLeft.shape[0]):
nextState=copy(state)
nextState[rowsLeft[i],columnsLeft[i]]=maxp
#print 'in max currently the Nextstate is ',nextState,'\n\n'
Nutility,Nstate=minimax(nextState,alpha,beta,False,depth-1,maxp,minp)
if Nutility > utility:
utility=Nutility
returnState=copy(nextState)
if utility>alpha:
alpha=utility
if alpha >=beta :
#print 'pruned'
break;
#print 'for max the best move is with utility ',utility,' n state ',returnState
return utility,returnState
else:
utility=inf
for i in range(0,rowsLeft.shape[0]):
nextState=copy(state)
nextState[rowsLeft[i],columnsLeft[i]]=minp
#print 'in min currently the Nextstate is ',nextState,'\n\n'
Nutility,Nstate=minimax(nextState,alpha,beta,True,depth-1,maxp,minp)
if Nutility < utility:
utility=Nutility
returnState=copy(nextState)
if utility< beta:
beta=utility
if alpha >=beta :
#print 'pruned'
break;
return utility,returnState
def checkGameOver(state):
stateCopy=copy(state)
value=utilityOfState(stateCopy)
if value >=1000:
return 1
return -1
def main():
num=input('enter player num (1st or 2nd) ')
value=0
global board
for turn in range(0,rows*cols):
if (turn+num)%2==1: #make the player go first, and make the user player as 'X'
r,c=[int(x) for x in raw_input('Enter your move ').split(' ')]
board[r-1,c-1]=1
printBoard()
value=checkGameOver(board)
if value==1:
print 'U win.Game Over'
sys.exit()
print '\n'
else: #its the computer's turn make the PC always put a circle'
#right now we know the state if the board was filled by the other player
state=copy(board)
value,nextState=minimax(state,neg_inf,inf,True,2,2,1)
board=copy(nextState)
printBoard()
print '\n'
value=checkGameOver(board)
if value==1:
print 'PC wins.Game Over'
sys.exit()
print 'Its a draw'
if __name__ == "__main__":
main()
Applications
Its major applications are in game of chess. Stockfish (chess) is a C++ open source chess program that implements the Alpha Beta pruning algorithm. Stockfish is a mature implementation that is rated as one of the strongest chess engines available today as evidenced by it winning the Top Chess Engine Championship in 2016 and 2017.
One more interesting thing to notice is that implementations of alpha-beta pruning can often be delineated by whether they are "fail-soft," or "fail-hard." The pseudo-code illustrates the fail-soft variation. With fail-soft alpha-beta, the alphabeta function may return values (v) that exceed (v < α or v > β) the α and β bounds set by its function call arguments. In comparison, fail-hard alpha-beta limits its function return value into the inclusive range of α and β.
Questions
What is the depth of a standard tic-tac-tow game?
Further Reading
-
Application of this pruning in Negamax algo: Research Paper by Ashraf M. Abdelbar
-
Detailed semantics by Donald E. Knuth and Ronald W. Moore
