
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we have covered the concept of how Backtracking help us to solve Game Tree. We will solve the Game Tree Problem by making use of the Minimax Algorithm. We have presented the Time and Space Complexity for various cases.
Table of contents:
- Introduction
- Solving Game Tree
- Time and Space Complexity
- Game tree of other games
- Conclusion
Introduction
Searching through Game Tree is the core of board-game artificial intelligence. Consider how humans play a game of strategy. A possible move for our next turn is the first thing we consider. We need to think about how our opponent will respond, then figure out how we would respond to that. We try to read out the variation and see if it's a good result. We backtrack and look at a different variation to see if it was better. This is a description of how the tree-search algorithms are used in the game AI. Humans can only keep a few changes in their heads at a time, while computers can juggle millions. Humans use their intuition to make up for their lack of computing power. Chess and Go players who are experienced can spot a few moves ahead that are worth looking into.
The course of the game is determined by the players decisions in a deterministic game. Rolling dice or shuffling cards are examples of randomness involved in a non-deterministic game.
The full game state can be seen by both players at all times in perfect information games. Everyone has their cards visible on the table or the board. Each player can only see a small part of the game state in hidden information games. In card games, players are dealt a few cards and can't see what the other players are holding. Hidden information games appeal to players because they have to guess what the other players know based on their decisions.
Solving Game Tree
To program a computer to play a game, we have to consider how humans would make a similar decision. The strategy call minimaxing can be applied. You are trying to maximize your score while your opponent is trying to reduce it. Let's see how it works.
Steps
- The game is played by two players, Max and Min in the Minimax algorithm.
- A deep-first search is performed for the exploration of the entire game tree.
- At the terminal node, if it is Max Player turn, the player will chose the action that lead to the maximum benefit.
- The algorithm will then backtrack and it is Min Player turn, the player will chose the action that lead to the minimum benefit.
Let's take a closer look at the algorithm.
Pseudocode
minimax(position, maximizingPlayer)
if depth == 0
return static_evaluation_of_position
else
for each child of position
depth = get_depth(child)
key, value = minimax(child)
leaf_data_dict[key] = value
return compare_node(leaf_data_dict, depth)
compare_node(leaf_data_dict, depth)
if depth is even
mini_max_eval = min(leaf_data_dict)
else
min_max_eval = max(leaf_data_dict)
return mini_max_eval
Implementation
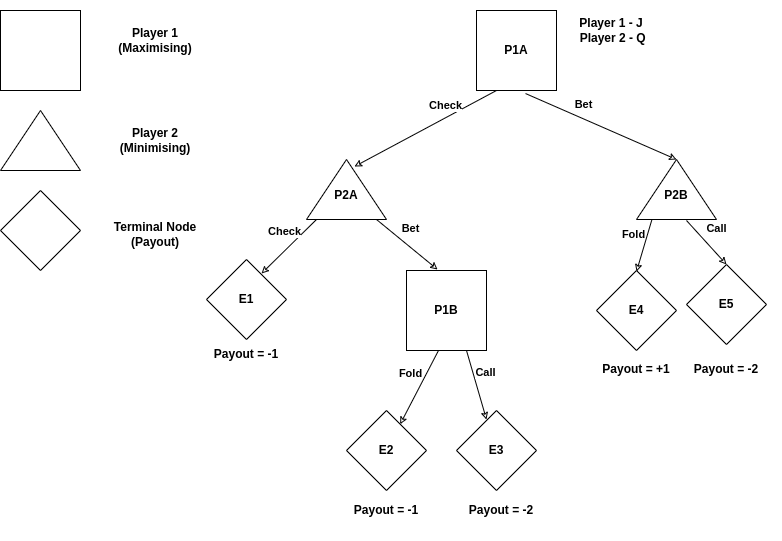
To illustrate how this algorithm work in actual game, let say there is only 3 cards involved, KQJ, whereby the ranking of K > Q and Q > J. At the beginning ot the game, each player put in an ante bet of 1 unit. Player 1 (Maximising) draws the card J. For the purpose of this example, let assume Player 1 happened to see that Player 2 draw the card Q. At showdown, Player 1 would lose to Player 2. However, Player 1 could bluff his way by betting in hope that Player 2 will fold. However he will risk 2 units instead of 1 units. Minimax algorithm could help Player 1 find the optimal path to take.
We import the treelib module to allow us to use the tree data structure. Next the class TheNode stores additional information about the node in the game tree, such as the label, unique idenitifier ID, action for player to take and the static evaluation (value).
The add_node() function specify the node label, identifier, additional data stored in the object gt_node and the parent id of the node(if any). The create_tree() function call the add_node() function to generate the game tree.
import treelib as tl
class TheNode(object):
def __init__(self, label, id, action, eval):
self.label = label
self.id = id
self.action = action
self.eval = eval
def add_node(label, id, parent=None, action=None, eval=0):
gt_node = TheNode(label, id, action, eval)
tree.create_node(tag=label, identifier=id, data=gt_node, parent=parent)
def create_tree():
add_node("P1A", "p1a", None, "Gametree Decision")
add_node("P2A", "p2a", "p1a", "CHECK")
add_node("E1", "e1", "p2a", "CHECK", -1)
add_node("P1B", "p1b", "p2a", "BET")
add_node("E2", "e2", "p1b", "FOLD", -1)
add_node("E3", "e3", "p1b", "CALL", -2)
add_node("P2B", "p2b", "p1a", "BET")
add_node("E4", "e4", "p2b", "FOLD",1)
add_node("E5", "e5", "p2b", "CALL",-2)
The minimax() function is a recursive function that takes in the node_id value, which is the position to start evaluating the game tree from. First we declare the base case scenario, if the node is the leaf node, the function will return the static evaluation of the node (payout value).
Otherwise, the function will performed a depth first search of the game tree. It will loop through every child nodes and perform a minimax() function on the child nodes. The payout value and the node label will be stored in the dictionary leaf_data. Next it will called the compare_node() to perform an comparison of the payout value.
def minimax(node_id):
# base case, if no sub nodes, just return the value
game_node = tree.get_node(node_id)
if game_node.is_leaf():
return [], game_node.data.eval
else:
leaf_data = {}
key = []
child_list = tree.children(node_id)
for child in child_list:
depth = tree.depth(child)
key, value = minimax(child.identifier)
#add eval data to dictionary
if child.is_leaf():
leaf_data[child.data.label] = child.data.eval
else:
# key, value = eval
leaf_data[key[0]] = value
return compare_node(leaf_data, key, depth)
In the compare_node() function, if the depth where the node is located at is even, it will return the Min value and label of the leaf_data dictionary, If the depth is odd, it will return the Max value and label of the leaf_data dictionary.
def compare_node(leaf_data, key, depth):
if (depth % 2) == 0:
key.insert(0, min(leaf_data, key=leaf_data.get))
mini_max_eval=leaf_data[min(leaf_data, key=leaf_data.get)]
print(f"[Minimize] lowest of {leaf_data}")
print(f"Choice selected will be {key[0]} : {mini_max_eval}")
else:
key.insert(0, max(leaf_data, key=leaf_data.get))
mini_max_eval=leaf_data[max(leaf_data, key=leaf_data.get)]
print(f"[Maximize] highest of {leaf_data}")
print(f"Choice selected will be {key[0]} : {mini_max_eval}")
print("=============================================")
return key, mini_max_eval
The display_result function will print out the decision path taken to reach the optimal result.
def display_result(choice):
solution = []
for node in tree.rsearch(choice):
solution.insert(0, tree[node].data.action + " - " + tree[node].tag)
print (f"\n{solution}")
Below is the driver code needed to create the game tree and run the evaluation to determine the optimal decision for Player 1 to take.
if __name__ == '__main__':
tree = tl.Tree()
create_tree()
# set key to True so that Tree is printed in the order it is inserted and not sorted by alphabetical order
tree.show(key = lambda x : True, line_type="ascii-em")
node_id = "p1a"
eval = minimax(node_id)
choice = eval[0][0].lower()
display_result(choice)
Once we run the code, we should see the following output. From the result, we can see that Player 1 should avoid bluffing and risking losing 2 units. The optimal decision taken will result in the loss of 1 unit.
P1A
╠══ P2A
║ ╠══ E1
║ ╚══ P1B
║ ╠══ E2
║ ╚══ E3
╚══ P2B
╠══ E4
╚══ E5
[Maximize] highest of {'E2': -1, 'E3': -2}
Choice selected will be E2 : -1
=============================================
[Minimize] lowest of {'E1': -1, 'E2': -1}
Choice selected will be E1 : -1
=============================================
[Minimize] lowest of {'E4': 1, 'E5': -2}
Choice selected will be E5 : -2
=============================================
[Maximize] highest of {'E1': -1, 'E5': -2}
Choice selected will be E1 : -1
=============================================
['Gametree Decision - P1A', 'CHECK - P2A', 'CHECK - E1']
Here is the entire code block for reference
import treelib as tl
class TheNode(object):
def __init__(self, label, id, action, eval):
self.label = label
self.id = id
self.action = action
self.eval = eval
def add_node(label, id, parent=None, action=None, eval=0):
gt_node = TheNode(label, id, action, eval)
tree.create_node(tag=label, identifier=id, data=gt_node, parent=parent)
def create_tree():
add_node("P1A", "p1a", None, "Gametree Decision")
add_node("P2A", "p2a", "p1a", "CHECK")
add_node("E1", "e1", "p2a", "CHECK", -1)
add_node("P1B", "p1b", "p2a", "BET")
add_node("E2", "e2", "p1b", "FOLD", -1)
add_node("E3", "e3", "p1b", "CALL", -2)
add_node("P2B", "p2b", "p1a", "BET")
add_node("E4", "e4", "p2b", "FOLD",1)
add_node("E5", "e5", "p2b", "CALL",-2)
def minimax(node_id):
# base case, if no sub nodes, just return the value
game_node = tree.get_node(node_id)
if game_node.is_leaf():
return [], game_node.data.eval
else:
leaf_data = {}
key = []
child_list = tree.children(node_id)
for child in child_list:
depth = tree.depth(child)
key, value = minimax(child.identifier)
#add eval data to dictionary
if child.is_leaf():
leaf_data[child.data.label] = child.data.eval
else:
# key, value = eval
leaf_data[key[0]] = value
return compare_node(leaf_data, key, depth)
def compare_node(leaf_data, key, depth):
if (depth % 2) == 0:
key.insert(0, min(leaf_data, key=leaf_data.get))
mini_max_eval=leaf_data[min(leaf_data, key=leaf_data.get)]
print(f"[Minimize] lowest of {leaf_data}")
print(f"Choice selected will be {key[0]} : {mini_max_eval}")
else:
key.insert(0, max(leaf_data, key=leaf_data.get))
mini_max_eval=leaf_data[max(leaf_data, key=leaf_data.get)]
print(f"[Maximize] highest of {leaf_data}")
print(f"Choice selected will be {key[0]} : {mini_max_eval}")
print("=============================================")
return key, mini_max_eval
def display_result(choice):
solution = []
for node in tree.rsearch(choice):
solution.insert(0, tree[node].data.action + " - " + tree[node].tag)
print (f"\n{solution}")
if __name__ == '__main__':
tree = tl.Tree()
create_tree()
# set key to True so that Tree is printed in the order it is inserted and not sorted by alphabetical order
tree.show(key = lambda x : True, line_type="ascii-em")
node_id = "p1a"
eval = minimax(node_id)
choice = eval[0][0].lower()
display_result(choice)
Time and Space Complexity
Time Complexity: O(b^d), where b refer to the branching factor. In this example, our branching factor is 2, at each node is there is 2 different decision to choose form. d refer to the depth of the game tree. In this example, the depth of the game tree is 3.
Space Complexity: O(b*d)
Game tree of other games
Tic-Tac-Toe
- The goal of the game is to get three in a row on a 3 x 3 board.
- The first and second players are known as
XandO. - The players take turn to place Xs and Os on the game board until the one player has three in a row or all nine squares are filled.
- In the event that no one has three in a row, the game reach stalemate and the result is a draw.
| Tic-Tac-Toe Game Tree |
|---|
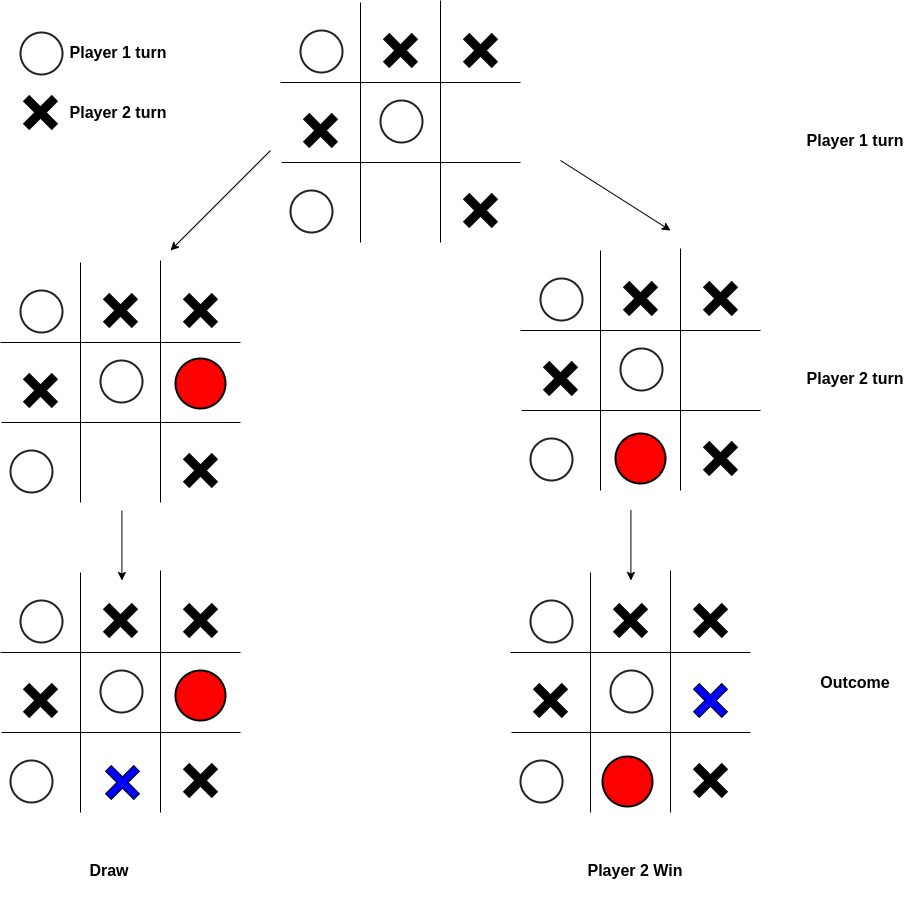 |
Connect Four
- Just like tic tac toe, you need to connect four colored checker pieces in a row to win Connect Four.
- This can be done in three different ways, horizontally, vertically or diagonally.
- Each player will drop one piece of checker at a time.
- You can either build your row or stop your opponent from getting four in a row.
| Connect Four Game Tree |
|---|
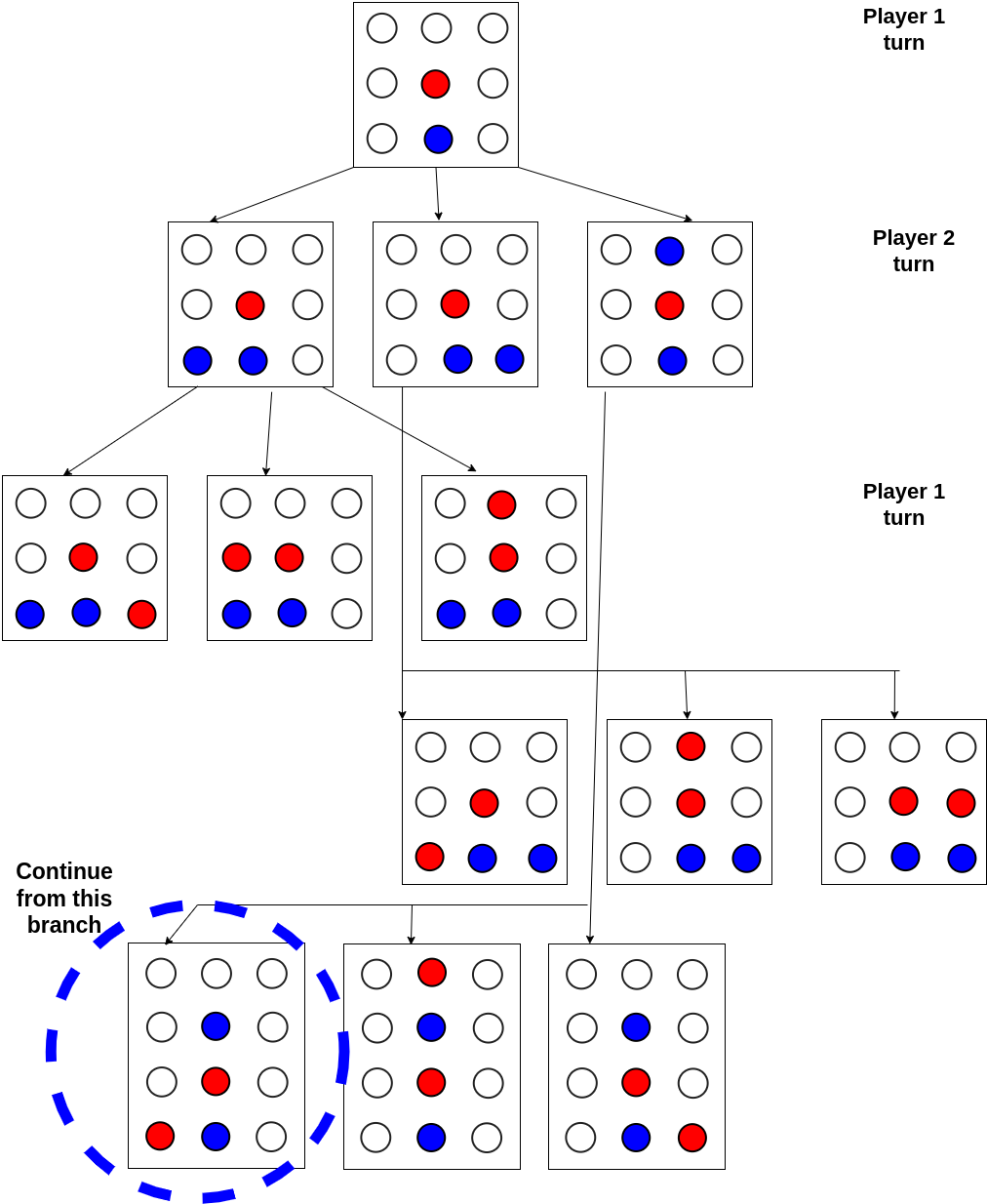 |
| Connect Four Game Tree |
|---|
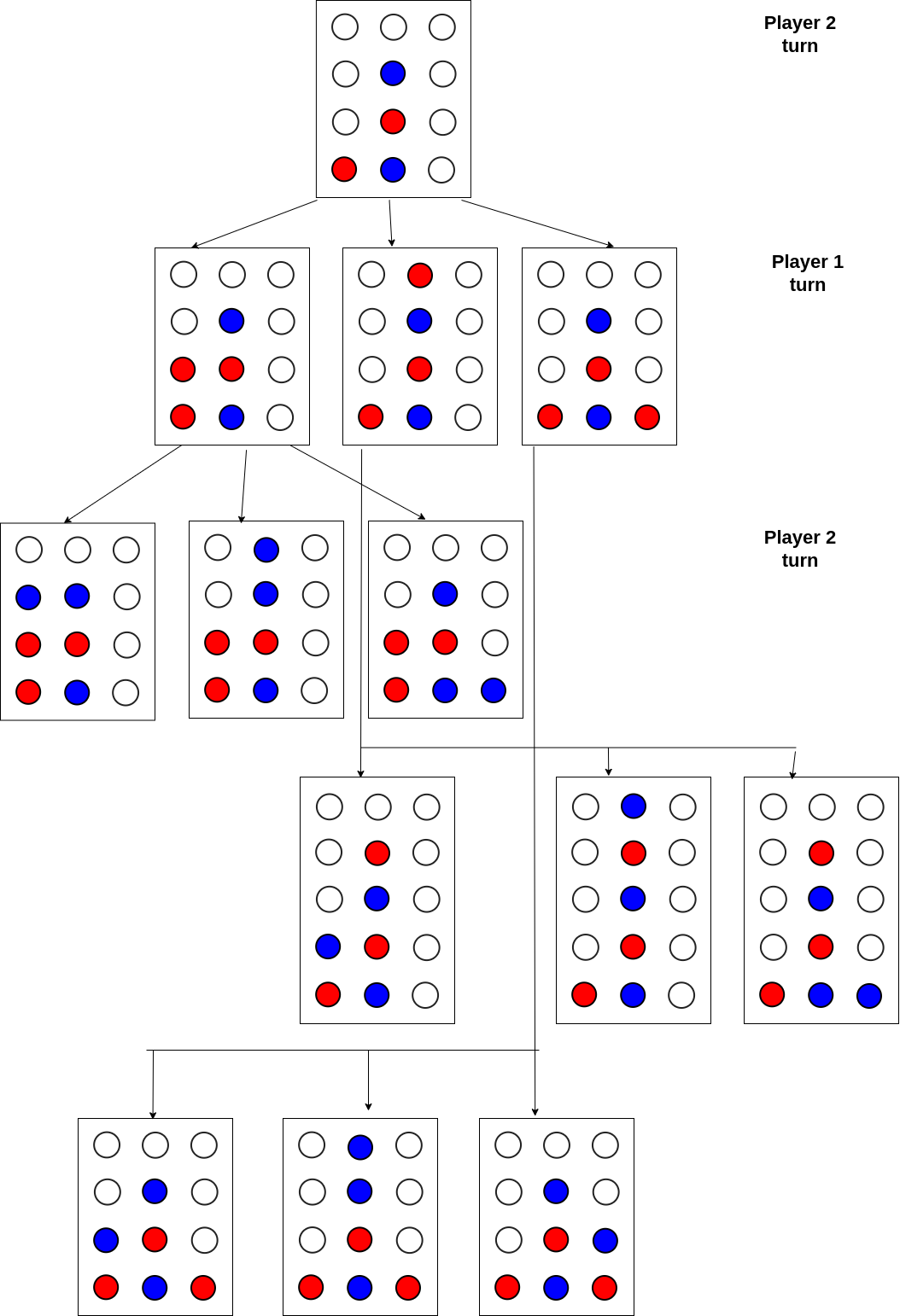 |
Conclusion
Minimax algorithm can be used to solve game tree of deterministic, perfect information games such as Chess and Checkers.
Consider using the counterfactual regret minimization algorithm in games like rock-paper-scissors and Poker which are non-deterministic and hidden information in nature.
With this article at OpenGenus, you must have the complete idea of how Backtracking help us to solve Game Tree.
