Nimber Arithmetic : A deeper dive in Nim

Reading time: 25 minutes | Coding time: 10 minutes

Algorithm

We will be discussing the nim-addition and nim-multiplication in deeper context with how they are implemented in Combinatory Game Theory (in Applications). But before we begin our journey, allow me to introduce you to 2 type of impartial game positions :

• A Game is in P-Position if the Player who just took the current turn wins.
• A Game is in N-Position if the Player after the player who took the current turn wins.

Nim addition

That being said, let's now discuss nim-addition

Nimber addition (also known as nim-addition) can be used to calculate the size of a single nim heap equivalent to a collection of nim heaps. It is defined recursively by:

$$\alpha \oplus \beta = mex ( \{ \alpha^, \oplus \beta : \alpha^, < \alpha \} \bigcup \{ \alpha \oplus \beta^, : \beta^, < \beta \} ) $$

For finite ordinals, the nim-sum is easily evaluated on a computer by taking the bitwise exclusive or (XOR, denoted by ⊕) of the corresponding numbers.

The key operation in the solution to Nim is binary addition without carrying.To add two numbers in this manner, first write out their binary expansions,and then take the exclusive or (XOR) of the two numbers bit by bit:

In the XOR operation, 1 + 1 = 0 = 0 + 0, 1 + 0 = 1 = 1 + 0. Another way to look at it is that if you are adding an odd number of ones the answer is 1, an even number of ones gives 0. We will write this kind of addition of two numbers x and y as x ⊕ y. But, in practical game, you'd most probably start off with 2 or more than 2 heaps , what then?

heaps = [] //Array of numbers representing objects in heaps
nimSum = 0
for (int i = 0 ; i < len(heaps); i++){
    nimSum = nimSum ^ heaps[i]
}
print (nimSum)

This Algorithm should work fine in all cases. Given below is one nim-addition matrix:

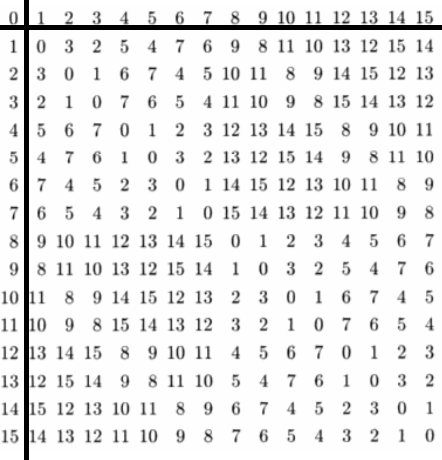
Nim multiplication

Now, moving on to nim-multiplication:

Nimber multiplication is defined recursively by

$$\alpha * \beta = mex ( \{ \alpha^, \beta \oplus \alpha \beta^, \oplus \alpha^, \beta^, : \alpha^, < \alpha , \beta^, < \beta \} ) $$

First of all, let me make it clear that this method is not really famous as the latter one with not many applications, neverthless, to give you a basic idea of it's non intutiveness I would like you to have a look at this python snippet :

f = lambda x,y:min(set(range(x*y+1))-{f(i%x,i/x)^f(x,i/x)^f(i%x,y)for i in range(x*y)})

which implements the recursive multiplication like this :

// Here * denotes nim multiplication
6 * 13
= (4 + 2) * (8 + 4 + 1)
= (4 + 2) * ((4 * 2) + 4 + 1)
= (4 * 4 * 2) + (4 * 2 * 2) + (4 * 4) + (4 * 2) + (4 * 1) + (2 * 1)
= (6 * 2) + (4 * 3) + 6 + 8 + 4 + 2
= ((4 + 2) * 2) + 12 + 6 + 8 + 4 + 2
= (4 * 2) + (2 * 2) + 12 + 6 + 8 + 4 + 2
= 8 + 3 + 12 + 6 + 8 + 4 + 2
= 15

Complexity

• For Nim Addition: O(N) {where N is number of heaps}
• For Nim Multiplication: Exponential Function Similar to the recursive definition

Implementations

• Python: Nimber Matrix Display
• Python: Win or Lose

    def get_matrix(n):
    main_matrix = [[0 for i in range(n)] for j in range(n)]
    for i in range(n):
        main_matrix[0][i] = i
        main_matrix[i][0] = i
    for i in range(1,n):
        for j in range(1,n):
            #print(" Performing {}^{} at ({},{})".format(x[0][j],x[i][0],i,j))
            main_matrix[i][j] = main_matrix[0][j]^main_matrix[i][0]
    return main_matrix
def get_nimber(matrix):
    for i in range(1,len(matrix[0])):
        for j in range(1,len(matrix[0])):
            if matrix[i][j] > (max(matrix[0])/2):
                matrix[i][j] = "."
            else:
                matrix[i][j] = "-"
    for i in range(len(matrix[0])):
        print(*matrix[i])
my_matrix = get_matrix(16)
get_nimber(my_matrix)
   

    import functools
    MISERE = 'misere'
    NORMAL = 'normal'
    def nim(heaps, game_type):
        """
        Computes next move for Nim, for both game types normal and misere.
        Assumption : Both players involved would play without making mistakes.
        if there is a winning move:
            return tuple(heap_index, amount_to_remove)
        else:
            return "You will lose :("
        """
        print(game_type, heaps, end=' ')
        is_misere = game_type == MISERE
        endgame_reached = False
        count_non_0_1 = sum(1 for x in heaps if x > 1)
        endgame_reached = (count_non_0_1 <= 1)
        # nim sum will give the correct end-game move for normal play but
        # misere requires the last move be forced onto the opponent
        if is_misere and endgame_reached:
            moves_left = sum(1 for x in heaps if x > 0)
            is_odd = (moves_left % 2 == 1)
            sizeof_max = max(heaps)
            index_of_max = heaps.index(sizeof_max)
            if sizeof_max == 1 and is_odd:
                return "You will lose :("
            # reduce the game to an odd number of 1's
            return index_of_max, sizeof_max - int(is_odd)
        nim_sum = functools.reduce(lambda x, y: x ^ y, heaps)
        if nim_sum == 0:
            return "You will lose :("
        # Calc which move to make
        for index, heap in enumerate(heaps):
            target_size = heap ^ nim_sum
            if target_size < heap:
                amount_to_remove = heap - target_size
                return index, amount_to_remove
    if __name__ == "__main__":
        import doctest
        doctest.testmod()       
   

Applications in Game of Nim

Now, about the applications of the above discussed two arithmetic sequences. We can use Nimber Addition to solve the famous game of Nim, So, how do we do it?

Notice that if we take the sum of all the nim-heaps, at the end the nimsum of all the heaps is equal to 0 (since adding 0 together any number of times gives 0). But there are other times that the nim-sum can be 0. Note that any x⊕x = 0, since any number XORed with itself is 0.

So, the winning strategy is easily :

• Whenever possible, reduce the heaps to two non-zero heaps containing the same number of coins each. This obviously has a nim-sum of 0.Now just mimic your opponent’s move each time on the opposite heap to keep the two heaps equal until you are able to take the final coin.

• Since doing binary addition is kind of hard to do in your head for large numbers, a more feasible strategy is often needed. An easy way to think about making the nim-sum 0 is to always leave even subpiles of the powers of 2, starting with the largest power possible, where a subpile is a pile group of coins within a nim-heap. So for example, leave an even number of subpiles of 2, 4, 8, 16, etc. Any time there are an
  even number of piles of each power of 2, the nim-sum must be 0.

Now, if we look at the major application of Nim multiplication, it can be seen in this fun problem of Seating the first few Billion Knights

The odd Knight of the round table problem asks for a consistent placement of the n^th Knight in the row at an odd root of unity, compatible with the two different realizations of the algebraic closure of the field with two elements.

The first identifies the multiplicative group of its non-zero elements with the group of all odd complex roots of unity, under complex multiplication. The second uses Conway’s ‘simplicity rules’ in ONAG to define an addition and multiplication on the set of all ordinal numbers.

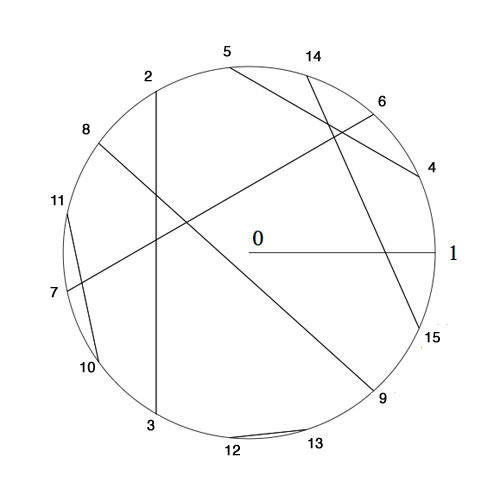
Here’s the seating arrangement for the first 15 knights. Conway proved that all finite ordinals smaller than 2²ⁱ form a subfield of F₂. The first non-trivial one being {0,1,2,3} with smallest multiplicative generator 2, whence we place Knight 2 at e^2iπ/3 and as 2²=3 (using 0 index of the {0,1,2,3}) we know where to place the third Knight.

The multiplicative algorithm utilized in a 2.4Ghz 2Gb MacBook with Sage 4.6 (According to the source documentation) is :

sage: R.< x,y,z,t,u >=GF(2)[]

sage: S.< a,b,c,d,e > =
R.quotient((x^2+x+1,y^2+y+x,z^2+z+x*y,t^2+t+x*y*z,u^2+u+x*y*z*t))

sage: (c*e+b*e+a*b*c*d+b*c*d+a*b*d+a+1)^65537
c^2 + b*d + a + 1

This utilizes Multiplicative Nimber to a certain extent!

Questions

Further Reading

• Detailed Article on Impartial Games:Reaserch Paper by MIT