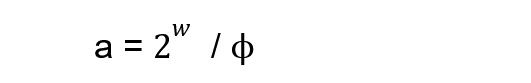Fibonacci Hashing

Table of Contents:

1. Introduction
2. Fibonacci Hashing
3. Code Implementation
4. Time Complexity
5. Comparisons
6. Applications

Reading time: 20 minutes

Introduction

In this article an underlooked kind of hash function is to be discussed, the Fibonacci Hashing. It is another form of multiplicative hashing function that is related to the golden ratio. This can be used as an alternative to other hashing functions; it's faster than sequential and binary searching. We will discuss how it works and implemented.

Fibonacci Hashing

First a brief refresher of hashing, it is one of the common searching algorithms. It uses hash tables which are data structures used to map keys to values. Using hash functions, hash values will be computed that are unique to each input. Then, each hash value is evenly spread across a hash table. There are different hash functions like division, mid square, folding and multiplication methods.

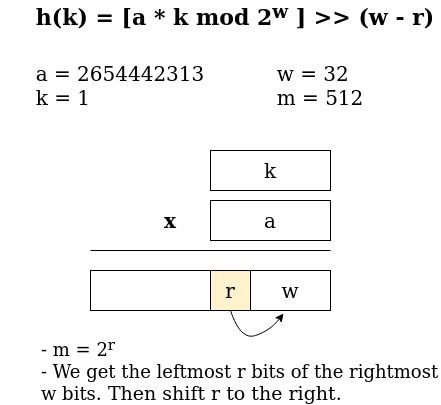
Fibonacci hashing is just another form of multiplicative hashing. In a multiplicative hashing function it uses the formula:

Where :
a = real number
w = word bit size
k = integer hash code
m = table size
m = 2^r

In fibonacci hashing instead of using a random integer as a it instead uses the golden ratio to divide 2^w.

where Φ = 1.618

For example, we have a hashtable with 512 slots and a hash value with 32 bit size word. Our value for a will be 2³² / Φ = 2654442313. The next process will be further discussed in the figure below

Let us try to implement this in C++ and see the results.

Code Implementation

   hash(int x) {
   // the value for a using golden ratio
   const std::uint32_t hash = 2654442313;
   const std::uint32_t y = x;
   // look at the top 3 bits of the hash value
   return (y * hash) >> (29);
   }

   int main() {

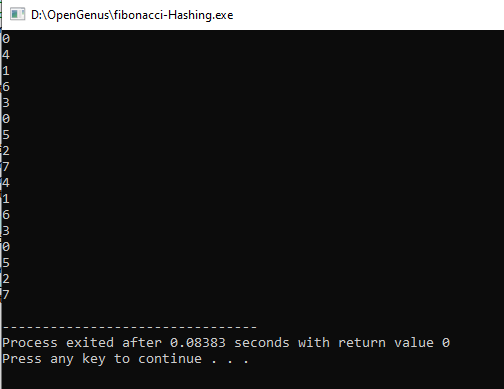
       for(int x=0; x<17; x++)  
       cout<<hash(x)<<endl;
       return 0;
   }

Output:

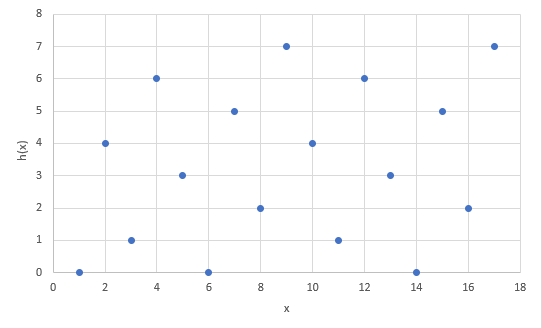
The output shows the top bits of each hash value so we can see the pattern of how fibonacci hashing works. Based on the results we can see that each value is evenly distributed. if we map this in a plot we can see the pattern.

Using the golden ratio in implementing multuplicative hashing helps in making consecutive keys distributed randomly but evenly.

Fibonacci hashing implements a faster hashing method and it produces a mixed up input patterns. However, it can cause high probability of collisions. One study implemented fibonacci hashing in a fast retrieval algorithm for fingerprint systems read it here. Fibonacci hashing is a good technique for storing large values in small spaces because it makes most of the space in a hash table.

Comparisons

There are other functions like Division method where h(k) = k mod m. This method can also be fast but is only best suited if m is prime and not too close to the power of 2. It will have problems if there are common factors between m and k and a table size with a power of two, it will be inefficient because it will only occupy/use half the table.

In comparison with multiplicative hashing using the golden ratio (h(k) = [ a*k mod 2^w] >> (w-r)), it works well with any table size. Using the golden ratio we already got the ideal value for a, therefore we already get an ideal value that will distribute consecutive keys evenly in the hash table.

Complexity

Space complexity: Θ(2m)
where m is the size of the table/list

Time complexity:

Depending on the probability of collisions, if less, then it will have average of Θ(1)
We should also consider the size of the table. if the the table is large then it will have less collisions, if small then there is a larger probability for collisions.

Applications

One study implemented fibonacci hashing in a fast retrieval algorithm for fingerprint systems read it here. Fibonacci hashing is a good technique for storing large values in small spaces because it makes most of the space in a hash table.

Fibonacci hashing is also used in a bioinformatics study. It was used for a protein family identification where each amino acid code is assigned to the Fibonacci numbers based on integer representations. read it here.