Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 15 minutes
It is a well-known fact that computers do not interpret numbers and other data like we do. They understand only binary, which is a dual system composed only of 0s and 1s. Programming languages provide an interface between the programmer and the system, converting whatever data we deal with into binary so that it can be processed by the computer, and then converting the result back into a form we can understand (usually decimal (base10) but also sometimes octal (base8) or hex (base16)).
In addition, most languages provide bitwise operators that allow you to perform certain operations at bit level. These operators and the supported operations are as follows:
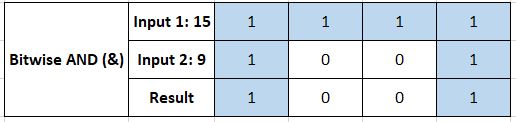
Bitwise AND (&)
This operator preforms a binary AND operation between the two operands. This means it compares the bits individually, the resultant bit mapping to 1 or true only if both bits fed to it are 1 as well.
Truth table:
| A | B | A & B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
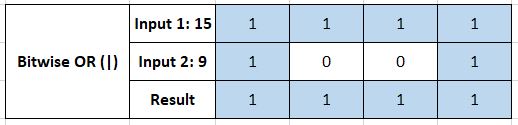
Bitwise OR (|)
This operator preforms a binary OR operation; the resultant bit mapping to 1 if one or more of the inputs to it is 1.
Truth table:
| A | B | A OR B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
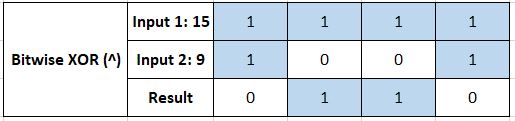
Bitwise XOR (^)
Performs the exclusive-OR or XOR operation; the resultant bit maps to 1 if both inputs have even number of ones (i.e. 0-1 or 1-0) but 0 otherwise.
Truth table:
| A | B | A ^ B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Bitwise Unary NOT (~)
Performs complementation or negation operation; inverts all the bits of the number, i.e. 0->1 and 1->0.
Truth table:
| A | ~ A |
|---|---|
| 0 | 1 |
| 1 | 0 |
Left Shift (<<)
Performs a shift or rotation by a specified number of positions. Every bit is moved left n positions. Further, the MSB (Most Significant Bit) is shifted to the LSB (Least Significant Bit) for every rotation. It is the equivalent of multiplying the number by 2 n times.
Truth table:
| A | A << 1 | A << 2 |
|---|---|---|
| 00010010 | 00100100 | 01001000 |
| 00111101 | 01111010 | 11110100 |
Right Shift (>>)
Every bit is moved right n positions. Further, in case of signed 2's complement numbers, the sign bit is moved into the MSB position. It is the equivalent of dividing the number by 2 n times.
| A | A >> 1 | A >> 2 |
|---|---|---|
| 00010010 | 00001001 | 00000100 |
| 00111101 | 00011110 | 00001111 |