Learn how to traverse a Binary Tree (Inorder , Preorder , Postorder)

Reading time: 35 minutes | Coding time: 5 minutes

In linear data structures like arrays and linked lists, we could traverse them in one way but in tree data structures like binary tree, we could traverse them in different ways. like:

1. depth first traversals
2. Breadth first traversals

• Depth first traversals of Binary tree:
  1. Inorder traversal
  2. Preorder traversal
  3. Postorder traversal

In this article we will learn three Depth first traversals namely inorder, preorder and postorder and their use. These three types of traversals generally used in different types of binary tree.

In summary:

• Inorder: left, root, right
• Preorder: root, left, right
• Postorder: left, right, root

Inorder Traversal

• In Inorder traversal we traverse from left-root-right.
• In this traversal left subtree visited first then the root and later the right subtree.
• remember that every node may represent a subtree itself.

Algorithm

Until all nodes are traversed

1. Recursively Traverse the left subtree
2. Visit the Root.
3. Recursively Traverse the right subtree.

Example of inorder traversal

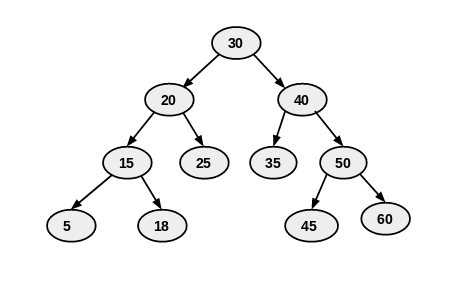
• we start recursive call from 30(root) then move to 20 (20 also have sub tree so apply in order on it),15 and 5.
• 5 have no child .so print 5 then move to it's parent node which is 15 print and then move to 15's right node which is 18.
• 18 have no child print 18 and move to 20 .print 20 then move it right node which is 25 .25 have no subtree so print 25.
• print root node 30 .
• now recursively traverse to right subtree of root node . so move to 40. 40 have subtree so traverse to left subtree of 40.
• left subtree of 40 have only one node which is 35. 35 had no further subtree so print 35. move to 40 and print 40.
• traverse to right subtree of 40. so move to 50 now have subtree so traverse to left subtree of 50 .move to 45 , 45 have no further subtree so print 45.
• move to 50 and print 50. now traverse to right subtree of 50 hence move to 60 and print 60.
• our final output is {5 , 15 , 18 , 20 , 25 , 30 , 35 , 40 , 45 , 50 , 60}

Application of inorder traversal

• In-order traversal is used to retrives data of binary search tree in sorted order.

Implementation of inorder traversal

class node:
    def __init__(self,key) :
        self.right=None
        self.left=None
        self.key=key
def Inorder(root): 
    if root: 
        Inorder(root.left) 
        print(root.key,end=" ")
        Inorder(root.right) 
root=node(30)
root.left=node(20)
root.right=node(40)
root.left.left=node(15)
root.left.right=node(25)       
Inorder(root)
print()

Preorder Traversal

• In Preorder traversal we traverse from root-left-right.
• In this traversal root visited first then the left subtree and later the right subtree.
• remember that every node may represent a subtree itself.

Algorithm of preorder traversal

Until all nodes are traversed

1. Visit the Root
2. Recursively Traverse the left subtree
3. Recursively Traverse the right subtree

Example of preorder traversal

• Start with root node 30 .print 30 and recursively traverse the left subtree.
• next node is 20. now 20 have subtree so print 20 and traverse to left subtree of 20 .
• next node is 15 and 15 have subtree so print 15 and traverse to left subtree of 15.
• 5 is next node and 5 have no subtree so print 5 and traverse to right subtree of 15.
• next node is 18 and 18 have no child so print 18 and traverse to right subtree of 20.
• 25 is right subtree of 20 .25 have no child so print 25 and start traverse to right subtree of 30.
• next node is 40. node 40 have subtree so print 40 and then traverse to left subtree of 40.
• next node is 35. 35 have no subtree so print 35 and then traverse to right subtree of 40.
• next node is 50. 50 have subtree so print 50 and traverse to left subtree of 50.
• next node is 45. 45 have no subtree so print 45 and then print 60(right subtree) of 50.
• our final output is {30 , 20 , 15 , 5 , 18 , 25 , 40 , 35 , 50 , 45 , 60}

Application of preorder traversal

• Preorder traversal is used to create a copy of the tree.
• Preorder traversal is also used to get prefix expression of an expression tree.

Implementation of preorder traversal

class node:
    def __init__(self,key) :
        self.right=None
        self.left=None
        self.key=key
def Preorder(root) :
    if root :
        print(root.key,end=" ")    
        Preorder(root.left) 
        Preorder(root.right)                 
root=node(30)
root.left=node(20)
root.right=node(40)
root.left.left=node(15)
root.left.right=node(25)       
Preorder(root)
print()

Postorder Traversal

• In Preorder traversal we traverse from left-right-root.
• In this traversal left subtree visited first then the right subtree and later the root.
• remember that every node may represent a subtree itself.

Algorithm of postorder traversal

Until all nodes are traversed

1. Recursively Traverse the left subtree
2. Recursively Traverse the right subtree.
3. Visit the Root.

Example of postorder traversal

• We start from 30, and following Post-order traversal, we first visit the left subtree 20. 20 is also traversed post-order.
• 15 is left subtree of 20 .15 is also traversed post order.
• 5 is left subtree of 15. 5 have no subtree so print 5 and traverse to right subtree of 15 .
• 18 is right subtree of 15. 18 have no subtree so print 18 and then print 15. post order traversal for 15 is finished.
• next move to right subtree of 20.
• 25 is right subtree of 20. 25 have no subtree so print 25 and then print 20. post order traversal for 20 is finished.
• next visit the right subtree of 30 which is 40 .40 is also traversed post-order(40 have subtree).
• 35 is left subtree of 40. 35 have no more subtree so print 35 and traverse to right subtree of 40.
• 50 is right subtree of 40. 50 should also traversed post order.
• 45 is left subtree of 50. 45 have no more subtree so print 45 and then print 60 which is right subtree of 50.
• next print 50 . post order traversal for 50 is finished.
• now print 40 ,and post order traversal for 40 is finished.
• print 30. post order traversal for 30 is finished.
• our final output is {5 , 18 , 15 , 25 , 20 , 35 , 45 , 60 , 50 , 40 , 30}

Application of postorder traversal

• Postorder traversal is used to delete the tree.
• Postorder traversal is also used to get the postfix expression of an expression tree.

Implementation of postorder traversal

class node:
    def __init__(self,key) :
        self.right=None
        self.left=None
        self.key=key
def Postorder(root) :
    if root :
        Postorder(root.left) 
        Postorder(root.right)
        print(root.key,end=" ")                     
root=node(30)
root.left=node(20)
root.right=node(40)
root.left.left=node(15)
root.left.right=node(25)       
Postorder(root)
print()

Summary

Time complexity for all three traversals (Inorder,Preorder,Postorder) is O(n) so it depends on the problem which traversal should be chosen.

In summary:

• Inorder: left, root, right
• Preorder: root, left, right
• Postorder: left, right, root