Van Emde Boas tree

Reading time: 30 minutes | Coding time: 15 minutes

Van Emde Boas tree is an associated array implemented through a multiway tree structure.

It is expected to perform five operations:

• find(k): Find the key k and the value it points to.
• predecessor(k): Return the largest key in domain less than or equal to k.
• successor(k): Return the smallest key in domain less greater or equal to k.
• insert(k): Insert a key k into the tree.
• delete(k): Delete the key k from tree.

Van Emde Boas tree or vEB stores the keys in a bounded universe and performs above operations in double logarithmic time complexity with respect to universe size.
vEB tree's other than being able to solve predecessor problem extremely fast, can also be used as an implementation of priority queue (which is faster than a heap implementation).

vEB tree for a universe U containing [0 ... U-1] is implemented by dividing the universe into √U vEB trees, where the i^th subtree would be responsible for universe of size √U containing the keys [(i)√U ... (i+1)√U-1]. The data structure is implemented recursively, where it shrinks by a factor of √U at every level.

The vEB tree is a modification of proto-vEB structure. A vEB tree stores following information:

• children array of size √U that points to children vEB trees. child i points to vEB tree responsible for the range
  [(i)√U ... (i+1)√U-1].
• min to store minimum element in the universe of the tree.
• max to store maximum element in the universe of the tree.
• summary, an auxillary vEB tree to keep track of which subtree/child is empty.
• A variable u to keep track of universe size.

When tree is empty, min and max are both NULL.
The element stored in min does not appear in any children trees, it is only stored at min, while element stored at max does.
When the universe size is 2, vEB does not need an array. It can just store the values in min and max attributes.
At the base level, a vEB tree is just a direct-addressing with added attributes.

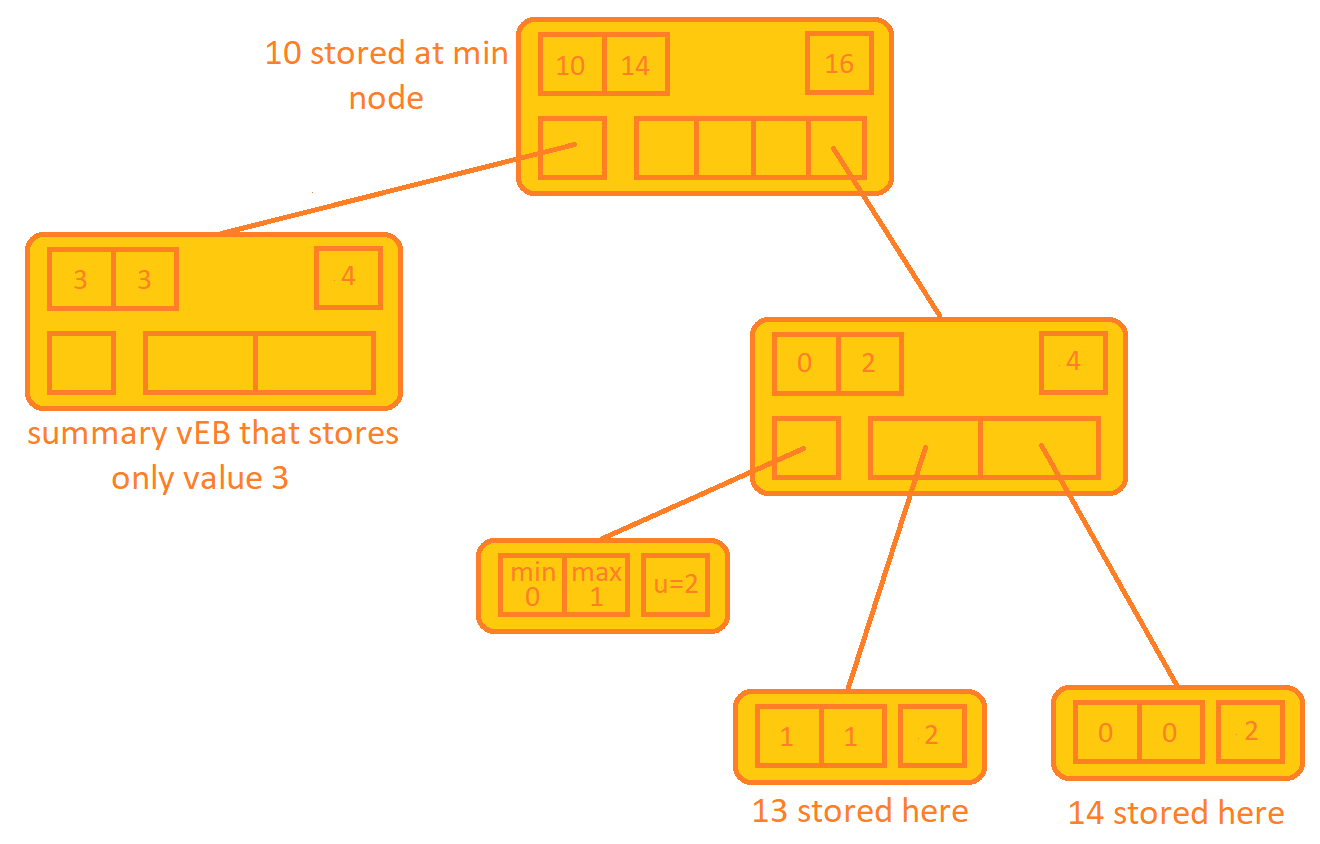
A vEB tree can ve represented as:

A vEB that stores values 10, 12, 13, 14.

Algorithm

• Because of the way tree is indexed, a key k belongs to any one of √U subtrees. Three function are used:

high(k, U) = floor(k/√U)

low(k, U) = k mod(√U)

index(k, k', U) = k√U + k'

The function high tells what subtree k belongs to
low tells the position of k in that subtree
The function index tells what is the actual key given the subtree number and position in the subtree.
The value of U is the universe size of tree in which the function is called. Also, it should be noted that universe size must be of form 2^2x.

Successor operation

• successor(T, k): This is a recursive funtion where T is the vEB tree to find the successor of k in T. The algorithm will be similar for predecessor.

function successor(T, k):
    if k < T.min:
        return T.min
    else if k > T.max:
        return T.u
        # universe size used as null value
    
    i = high(k, T.u)   # subtree index
    j = low(k, T.u)  # key for the subtree
    if j < T.children[i].max:
        return k - j + successor(T.children[i], j)
    # otherwise find next subtree for successor
    return k - j + T.children[successor(T.summary, i)].min

predecessor function is implmented similarly.

Insert operation

• insert(k):

function insert(T, k):
    # if tree is empty, i.e. first insertion
    if T.min > T.max:
        T.min = k
        T.max = k
        return
    
    # if key is new T.min, instead of k insert old T.min in subtrees
    # set k as new T.min
    if k < T.min:
        swap(k, T.min)
    
    # since T.max is also stored in subtrees, no need to swap
    if k > T.max:
        T.max = k
    
    # if at lowest vEB, i.e. the leaf tree
    if T.u == 2:
        # note that k can be 0 or 1
        T.max = k
        return
    i = high(k, T.u)   # subtree index
    j = low(k, T.u)  # key for the subtree
    insert(children[i], j)
    
    # if the recursive insertion created a new subtree, add it to summary vEB
    if children[i].max == children[i].min:
        insert(T.summary, i)

Delete operation

• delete(k):

function delete(T, k):
    # if only one element in tree
    if T.min == T.max:
        T.min = inf
        T.max = -inf
        return

    # if k is T.min, assign new value to it and return since min is not
    # stored in children
    if k == T.min:
        i = T.summary.min   # index of first subtree
        T.min = index(i, T.children[i].min, T.u)  # declared above
        return

    i = high(k, T.u)   # index of subtree that contains k
    j = low(k, T.u)  # key for the subtree
    
    # if last subtree
    if u == 2:
        if k == 1:
            if min == 1:
                min = T.u
                max = -1
            else if min == 0:
                max = 0
        else:    
            # i.e. k == 0
            if max == 0:
                min = T.u
                max = -1
            else if max == 1
                min = 1
        return
    
    delete(T.children[i], j)

    if T.children[i] is empty:
        delete(T.summary, i)

    # if deleted element was T.max
    if k == T.max:
        # if no subtrees exist, tree just has one element stored at t.min
        if T.summary is empty:
            T.max = T.min
        else:
            # else find new max element
            i = T.summary.max   # index of last subtree
            T.max = index(i, T.children[i].max, T.u)

Complexity

• Time complexity:
  1. Find: O(log₂log₂U)
  2. Successor, Predecessor: O(log₂log₂U)
  3. Insert: O(log₂log₂U)
  4. Delete: O(log₂log₂U)
• Space complexity: O(U)

Where U is universe size.

Implementations

C++ 11

/* 
 * Code for van emde boas tree. Try to implement function for predecessor as
 * an exercise.
 */

#include <cmath>
#include <iostream>
#include <vector>

class vEB
{
    int u;
    int min;
    int max;
    vEB *summary;
    std::vector<vEB *> children;

    int high(int k){
        int x = std::ceil(std::sqrt(u));
        return std::floor(k / x);
    }

    int low(int k){
        int x = std::ceil(std::sqrt(u));
        return k % x;
    }

    int index(int k, int kk){
        return (k * (int)std::sqrt(u)) + kk;
    }

public:

    vEB(int U){
        // u = std::pow(std::sqrt(U), 2);
        u = U;
        min = U;
        max = -1;
        
        if (u <= 2){
            summary = nullptr;
            children = std::vector<vEB *> (0, nullptr);
        }
        else{
            int children_count = std::ceil(std::sqrt(u));
            int children_size = std::ceil(u / std::sqrt(u));

            summary = new vEB(children_count);
            children = std::vector<vEB *> (children_count, nullptr);
            for(int i = 0; i < children_count; ++i){
                children[i] = new vEB(children_count);
            }
        }
    }

    void insert(int k){
        if(min > max){
            min = max = k;
            return;
        }

        if(k < min){
            int temp;
            temp = min;
            min = k;
            k = temp;
        }

        if(k > max)
            max = k;
        
        if(u == 2){
            max = k;
            return;
        }

        int i = high(k);
        int j = low(k);

        children[i]->insert(j);

        if(children[i]->max == children[i]->min)
            summary->insert(i);
    }

    void remove(int k){
        if(min > max)
            return;

        if(min == max){
            min = u;
            max = -1;
            return;
        }

        if(u == 2){
            if(k == 1){
                if(min == 1){
                    min = u;
                    max = -1;
                }
                else if(min == 0)
                    max = 0;
            }
            else
                if(max == 0){
                    min = u;
                    max = -1;
                }
                else if(max == 1)
                    min = 1;
            return;
        }

        if(k == min){
            int i = summary->min;
            min = index(i, children[i]->min);
            return;
        }

        int i = high(k);
        int j = low(k);

        children[i]->remove(j);

        if(children[i]->min > children[i]->max){
            summary->remove(i);
        }

        if(k == max){
            if(summary->min > summary->max){
                max = min;
            }
            else{
                i = summary->min;
                max = index(i, children[i]->max);
            }
        }
    }

    int getMin(){
        return min;
    }
    int getMax(){
        return max;
    }

    int universe(){
        return u;
    }

    int successor(int k){
        if(k <= min)
            return min;
        else if(k > max)
            return u;
        
        int i = high(k);
        int j = low(k);

        if(j <= children[i]->max){
            int res = children[i]->successor(j);
            if(res >= (u / (int)std::sqrt(u)))
                return u;
            return k - j + res;
        }
        else{
            int res = children[summary->successor(i)]->min;
            if(res >= children[summary->min]->u)
                return u;
            return index(summary->successor(i), res);
        }
    }
};

int main(){
    vEB tree(1 << 4);
    std::cout << "Insert 12, 10, 13, 14\n";
    tree.insert(12);
    tree.insert(10);
    tree.insert(13);
    tree.insert(14);
    std::cout << "Successor of 2 is\n";
    std::cout << tree.successor(2) << '\n';
    tree.remove(13);
    std::cout << "Removing 13. Now successor of 13 is\n";
    std::cout << tree.successor(13) << '\n';
    tree.remove(14);
    std::cout << "Removing 14. Now successor of 13 is\n";
    std::cout << tree.successor(13) << '\n';
    std::cout << "16, which is universe size, means no successor.\n";

    return 0;
}

Applications

• vEB trees were made specefically to solve predecessor problem in double logarithmic time.
• vEB trees can be used as extremely fast priority queues and find uses in routing applications.
• If universe size is reasonable, vEB trees are basically faster binary search trees.

References/ Further reading

• CLRS chapter 20 to know more about vEB trees and prototype structure, and motivations beind it.
• Lecture slides from stanford cs166.
• Lecture by Eric Demaine on youtube