
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 15 minutes
The Game of Life is a cellular automaton created in 1970 by the British mathematician John Horton Conway. The game is a zero-player game, where you include an initial input and watch how the board evolve through the generations and if the life will prosper or will be extinct over time.
Like a regular cellular automaton, the Game of Life works with a synchronous behavior on a 2-dimensional grid space which is governed by a simple set of rules who allows the cells to toggle between two states (live or dead). These rules recognize as neighbors the eight cells around the target cell, knowing as Moore neighborhood.
- If a dead cell has three neighbors, this cell becomes alive;
- If two or three neighbors are alive, this cell keeps alive;
- If a cell has less than two neighbors alive, this cell dies by solitude;
- If more than three neighbors are alive, this cell dies by overpopulation;
Only with these rules, we are ready to play the game. To be assured that our population stays alive we can insert as input a pattern that will not change over time. In the image below we have some samples of these static elements.
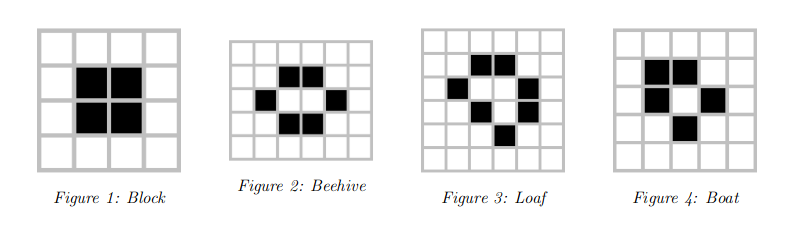
Simultaneously, we can produce structures capable of:
- change through time
- with a certain number of generations, return to your initial state.
These elements are known as oscillators. The most famous oscillators for the Game of Life are the blinker and toad shapes, illustrated below.
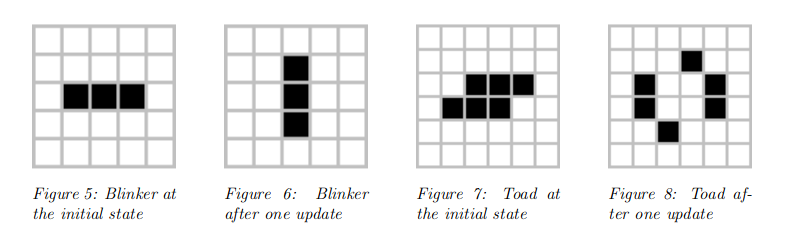
This structures can stay alive indefinitely. However, they are incapable of evolution without a kind of external interaction.
For this, we presented the third kind of shape commonly called spaceship or glider. This structure is similar to oscillators having an initial state and return to them after some number of generations. However, when a spaceship comes back to your initial shape, they are not on your initial location but slightly shifted from its original position.
That way, this kind of structure can travel through space in some defined direction.

Applications
Many mathematicians and scientist became interested in the model designed by John Conway despite the simplicity of the automaton. Since the creation, the Game of Life is used being the base to different studies who need to simulate scenarios with specified rules. Some examples of these studies are:
- Quantum mechanics;
- Music theory;
- Population studies;
References/ Further reading
Play John Conway’s Game of Life
The Game of Life and Other Cellular Automata - Mi Yu/Adam Reevesman
