
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 30 minutes
Jonh Von Neumann worked for years on a simple model for a logical cellular automaton with the purpose to build a self-replication machine. Wich logical organization an automaton will need to be able to control itself in a way that it reproduces itself? To answer that, Von Neumann thought on logical operations and states with different objectives, capable to construct and deconstruct other states for their own. This lead to Von Neumann Cellular System
Finite Automata
A Finite Automata are the base of a Turing Machine. This kind of automata operates deterministically, been represented by a set of states which follows some transition function until getting an output state. This transition from state to state occurs discreetly for each moment of time, changing to another one of the finite states.
To know what the next state, the transition function needs input data, which can be any character or symbol accepted for the function. Also, at least one output state is required since that state indicates a valid input for that automaton.
Von Neumann Cellular System
To represent a finite automaton on a cellular system, we can mark a finite area of the cellular space, specifies the states of the cells in this area and create a mechanism which simulates the automaton. The Von Neumann automaton has a total of 29 states for each cell.
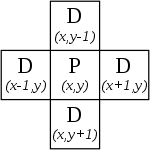
This cells can receive signals from the neighbors positioned in a 2D Cartesian grid, Von Neumann define as neighborhood (D) only the four cells who share a face with the target one (P), illustrated for the image below.
States
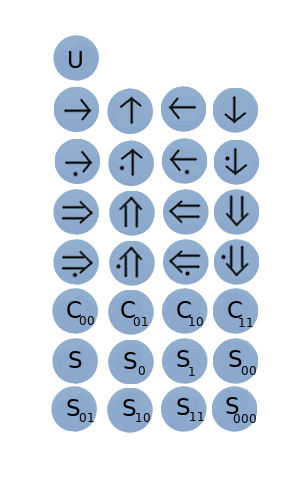
To maintain your simplicity, Von Neumann limited your automaton to only 29 states, is that the minimum to build a self-replication machine. This states can be divided into four groups:
- the blank state
- the transmission states
- the confluent states
- the transition states.
-
The blank state or unexcitable state (U) is the basic and initial state, when it is excited it will become one of the transmission states or a confluent state. If another state has been deconstructed, that cell returns to the blank state.
-
The transmission states behave like a conductor wire, where pulses and signals can move from a place to the other. They are sub-divided in ordinary transmission (represented by simple arrows in the four directions: → ↓ ← ↑) and special transmission (represented by double arrows). This separation is justified because of the deconstruct mechanism which will be discussed later. Each one of the directions has two states, the unexcited and excited one. Totalizing in all, we have 16 transmission states which transport binary pulses to the cell that it is pointing for. They can receive this signals from other transmission state or from a confluent state.
-
The confluent states (C) are four in total. This element can be used as a bridge for communication between the ordinary transmission states and the special transmission states. It also has a delay of one unit of time to receive the input and release from other states, the four Confluent States are all the combinations of 1's and 0's for two digits (C00 C01 C10, C11) representing this delay. To be excited, a confluent element has to receive a pulse from all the neighbors transmission states which are pointing at it, simulation a AND port (the transmission states simulated a OR port). After the delay, the state release the information at all the neighbors transmission states that are not pointing directly at it. Confluent states do not transmit information to another confluent state.
-
The transition states or sensitive states (S) are using to construct all the others starting from a blank state. The output state are created according to the signals that cell receive during its transition process. So, to be able to create all the nine quiescent states (C00 and the unexcited transmission states) there are eight transition states (S, S0, S00, S000, S01, S1, S10, S11)
Construction
What is the minimum number of states to build a self replication machine?
The construction mechanism starts when a blank state (U) is excited by a transmission state in your neighborhood. At this moment the cell becomes "sensitive" (S), passing through the transition states until stops in one of the ordinary or special transmission states, or in a confluent state. The chosen state is determined by the sequence of input signals that arrive on that cell. The options of that sequence can be represented by a binary tree.
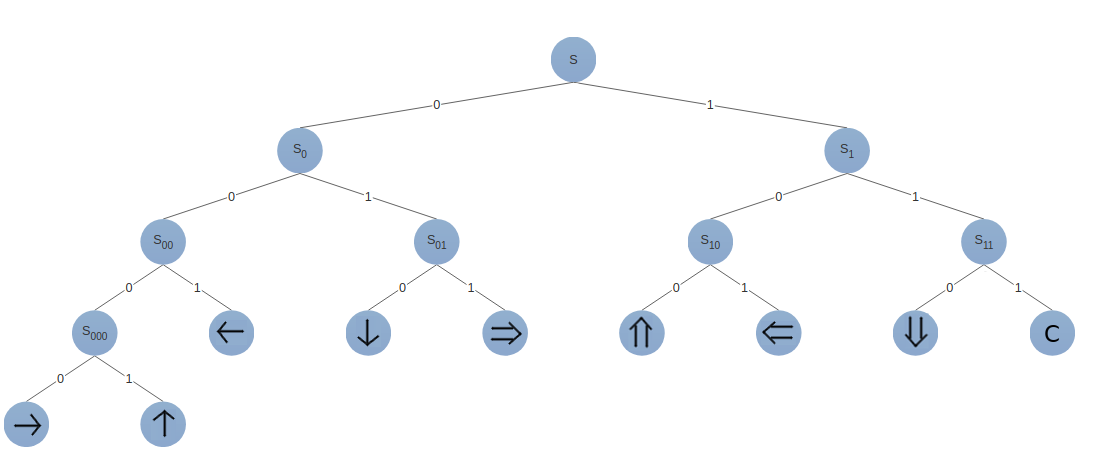
Note that one more unit of time is needed to construct the least-direction or the north-direction ordinary transmission states, the other states required just three cycles of input after the initial sensitization. Also, the "default" quiescent state in the construction is the least-direction ordinary transmission state (10000), requiring no input after the first signal.
Deconstruction
Von Neumann builds your automaton model to be able to deconstruct cells back to the blank state (U). Some additional rules determinate the situations where a cell will be destroyed.
- if a confluent state receives an input from a special transmission state that confluent state will be reduced to U.
- if an ordinary transmission state receive an input from a special transmission state that ordinary transmission state will be reduced to U.
- if a special transmission state receives an input from an ordinary transmission state that special transmission state will be reduced to U.
This deconstruction mechanism is why the Von Neumann Cellular Automaton model does not have a NOT port simulation in your states. The automata should have a quiescent state, if they have a NOT element there will be parts of the automata which will start a destruct each other.
Applications
This Von Neumann model is the original expression of cellular automaton. These mechanisms can be used to simulate real systems like:
- traffic modeling
- structural design
- fluid flow
- musical composition
