
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 30 minutes | Coding time: 15 minutes
Cohen Sutherland Algorithm is a line clipping algorithm that cuts lines to portions which are within a rectangular area. It eliminates the lines from a given set of lines and rectangle area of interest (view port) which belongs outside the area of interest and clip those lines which are partially inside the area of interest.
Example:
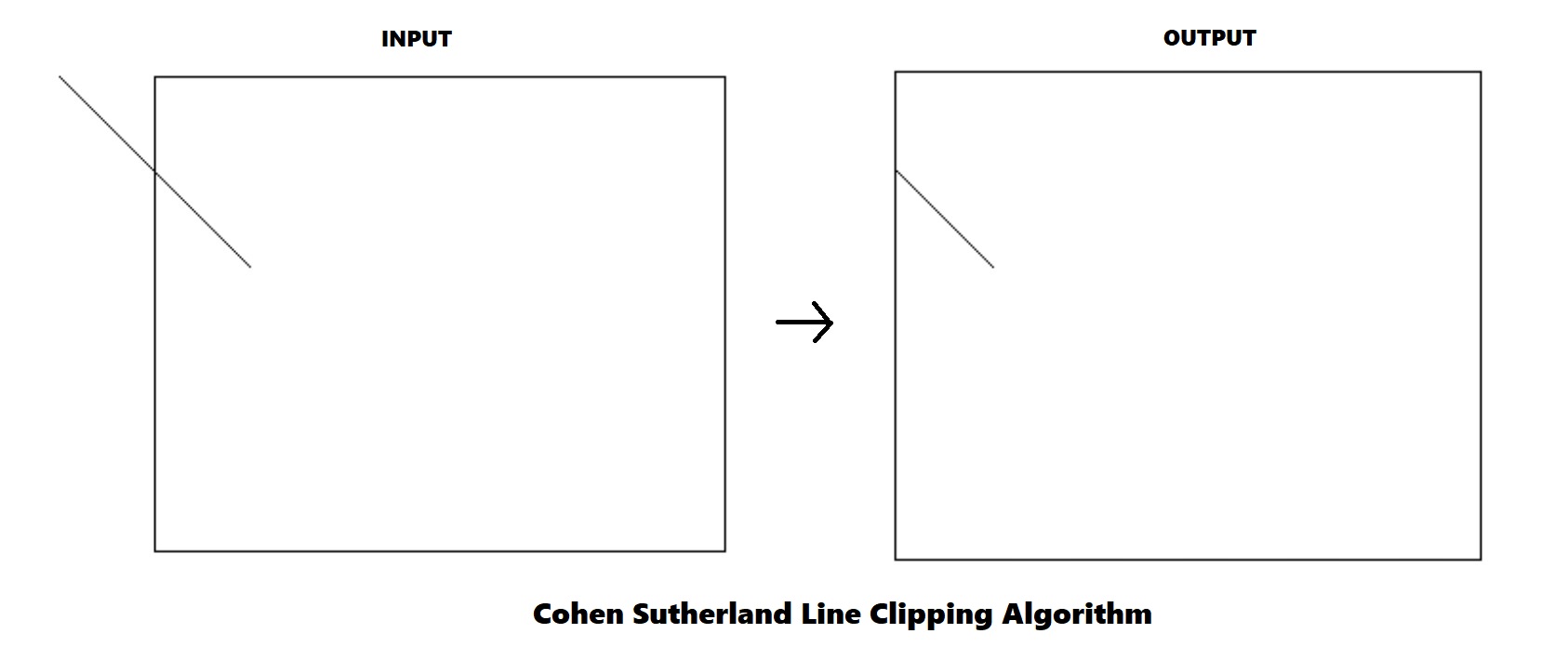
Algorithm
The algorithm divides a two-dimensional space into 9 regions (eight outside regions and one inside region) and then efficiently determines the lines and portions of lines that are visible in the central region of interest (the viewport).
Following image illustrates the 9 regions:
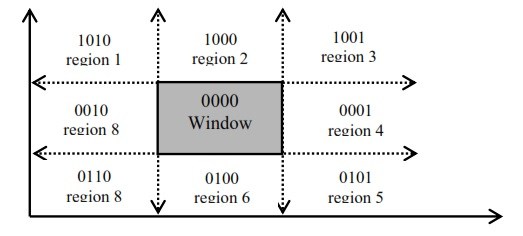
As you seen each region is denoted by a 4 bit code like 0101 for the bottom right region
Four Bit code is calculated by comparing extreme end point of given line (x,y) by four co-ordinates x_min, x_max, y_max, y_min which are the coordinates of the area of interest (0000)
Calculate the four bit code as follows:
- Set First Bit if 1 Points lies to left of window (x < x_min)
- Set Second Bit if 1 Points lies to right of window (x > x_max)
- Set Third Bit if 1 Points lies to bottom of window (y < y_min)
- Set Fourth Bit if 1 Points lies to top of window (y > y_max)

The more efficient Cohen-Sutherland Algorithm performs initial tests on a line to determine whether intersection calculations can be avoided.
Pseudocode
- Step 1 : Assign a region code for two endpoints of given line
- Step 2 : If both endpoints have a region code 0000 then given line is completely inside and we will keep this line
- Step 3 : If step 2 fails, perform the logical AND operation for both region codes.
- Step 3.1 : If the result is not 0000, then given line is completely outside.
- Step 3.2 : Else line is partially inside.
- Step 3.2.a : Choose an endpoint of the line that is outside the given rectangle.
- Step 3.2.b : Find the intersection point of the rectangular boundary (based on region code).
- Step 3.2.c : Replace endpoint with the intersection point and update the region code.
- Step 3.2.d : Repeat step 2 until we find a clipped line either trivially accepted or rejected.
- Step 4 : Repeat step 1 for all lines
What is the limitation of Cohen Sutherland algorithm?
Implementation
#include <iostream>
// Part of Cosmos by OpenGenus Foundation
class CohenSutherLandAlgo
{
private:
double x1,y1,x2,y2;
double x_max,y_max,x_min,y_min;
const int INSIDE = 0; // 0000
const int LEFT = 1; // 0001
const int RIGHT = 2; // 0010
const int BOTTOM = 4; // 0100
const int TOP = 8; // 1000
public:
CohenSutherLandAlgo()
{
x1 = 0.0;
x2 = 0.0;
y1 = 0.0;
y2 = 0.0;
}
void getCoordinates();
void getClippingRectangle();
int generateCode(double x, double y);
void cohenSutherland();
};
void CohenSutherLandAlgo::getCoordinates()
{
std::cout << "\nEnter Co-ordinates of P1(X1,Y1) of Line Segment : ";
std::cout << "\Enter X1 Co-ordinate : ";
std::cin >> x1;
std::cout << "\Enter Y1 Co-ordinate : ";
std::cin >> y1;
std::cout << "\nEnter Co-ordinates of P2(X2,Y2) of Line Segment : ";
std::cout << "\Enter X2 Co-ordinate : ";
std::cin >> x2;
std::cout << "\Enter Y2 Co-ordinate : ";
std::cin >> y2;
}
void CohenSutherLandAlgo::getClippingRectangle()
{
std::cout << "\nEnter the Co-ordinates of Interested Rectangle.";
std::cout << "\nEnter the X_MAX : ";
std::cin >> x_max;
std::cout << "\nEnter the Y_MAX : ";
std::cin >> y_max;
std::cout << "\nEnter the X_MIN : ";
std::cin >> x_min;
std::cout << "\nEnter the Y_MIN : ";
std::cin >> y_min;
}
int CohenSutherLandAlgo::generateCode(double x, double y)
{
int code = INSIDE; // intially initializing as being inside
if (x < x_min) // lies to the left of rectangle
code |= LEFT;
else if (x > x_max) // lies to the right of rectangle
code |= RIGHT;
if (y < y_min) // lies below the rectangle
code |= BOTTOM;
else if (y > y_max) // lies above the rectangle
code |= TOP;
return code;
}
void CohenSutherLandAlgo::cohenSutherland()
{
int code1 = generateCode(x1, y1); // Compute region codes for P1.
int code2 = generateCode(x2, y2); // Compute region codes for P2.
bool accept = false; // Initialize line as outside the rectangular window.
while (true)
{
if ((code1 == 0) && (code2 == 0))
{
// If both endpoints lie within rectangle.
accept = true;
break;
}
else if (code1 & code2)
{
// If both endpoints are outside rectangle,in same region.
break;
}
else
{
// Some segment of line lies within the rectangle.
int code_out;
double x, y;
// At least one endpoint lies outside the rectangle, pick it.
if (code1 != 0)
code_out = code1;
else
code_out = code2;
/*
* Find intersection point by using formulae :
y = y1 + slope * (x - x1)
x = x1 + (1 / slope) * (y - y1)
*/
if (code_out & TOP)
{
// point is above the clip rectangle
x = x1 + (x2 - x1) * (y_max - y1) / (y2 - y1);
y = y_max;
}
else if (code_out & BOTTOM)
{
// point is below the rectangle
x = x1 + (x2 - x1) * (y_min - y1) / (y2 - y1);
y = y_min;
}
else if (code_out & RIGHT)
{
// point is to the right of rectangle
y = y1 + (y2 - y1) * (x_max - x1) / (x2 - x1);
x = x_max;
}
else if (code_out & LEFT)
{
// point is to the left of rectangle
y = y1 + (y2 - y1) * (x_min - x1) / (x2 - x1);
x = x_min;
}
// Intersection point x,y is found.
// Replace point outside rectangle by intersection point.
if (code_out == code1)
{
x1 = x;
y1 = y;
code1 = generateCode(x1, y1);
}
else
{
x2 = x;
y2 = y;
code2 = generateCode(x2, y2);
}
}
}
if (accept)
{
std::cout <<"Line accepted from " <<"("<< x1 << ", "
<< y1 << ")" << " to "<< "(" << x2 << ", " << y2 << ")" << std::endl;
}
else
std::cout << "Line rejected" << std::endl;
}
int main()
{
CohenSutherLandAlgo c;
c.getCoordinates();
c.getClippingRectangle();
c.cohenSutherland();
return 0;
}
Complexity
The time and space complexity of Cohen Sutherland line clippling algorithm are:
- Worst case time complexity:
Θ(n) - Average case time complexity:
Θ(n) - Best case time complexity:
Θ(n) - Space complexity:
Θ(1)
where N is the number of lines
Further reading
For learning how to do line clipping for a ploygon area of interest, read:
- Cyrus Beck algorithm
- Sutherland Hodgman algorithm
