
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 35 minutes | Coding time: 15 minutes
Segment Tree is used to answer range queries in an array. The data structure can be extended to 2 dimensions to answer sub-matrix queries in logarithmic time. Some examples of these queries are :
- Maximum/minimum element in sub-matrix
- Sum of elements in sub-matrix
- XOR of elements is sub-matrix
The process to build a 2D segment tree is quite similar to process of building a 1D segment tree. Only difference is that every node in a 2D segment tree is a 1D segment tree in itself, so it can be called a segment tree of segment trees. 2D segment tree consumes more space than a 2D Fenwick tree so it is mostly used for cases where 2D Fenwick tree can't be used.
Building a 2D Segment Tree
A sum 2D segment tree will be considered here.
Consider the matrix:
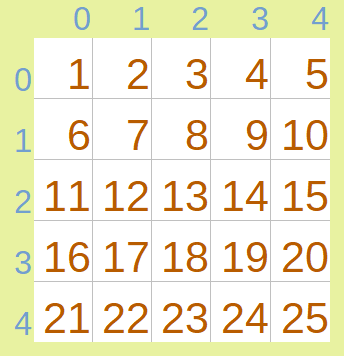
The general process while building a 2D segment tree for above 5 x 5 matrix would be :
- Start building a segment tree of segment trees either along x-axis or along y-axis of the matrix. We will build start building along y-axis. That means every node of 2D segment tree represents a segment tree of matrix elements along x-axis. Since segment tree is built in a bottom-up manner, we will first consider the leaf nodes. Each leaf nodes represents a segment tree for a row of matrix:
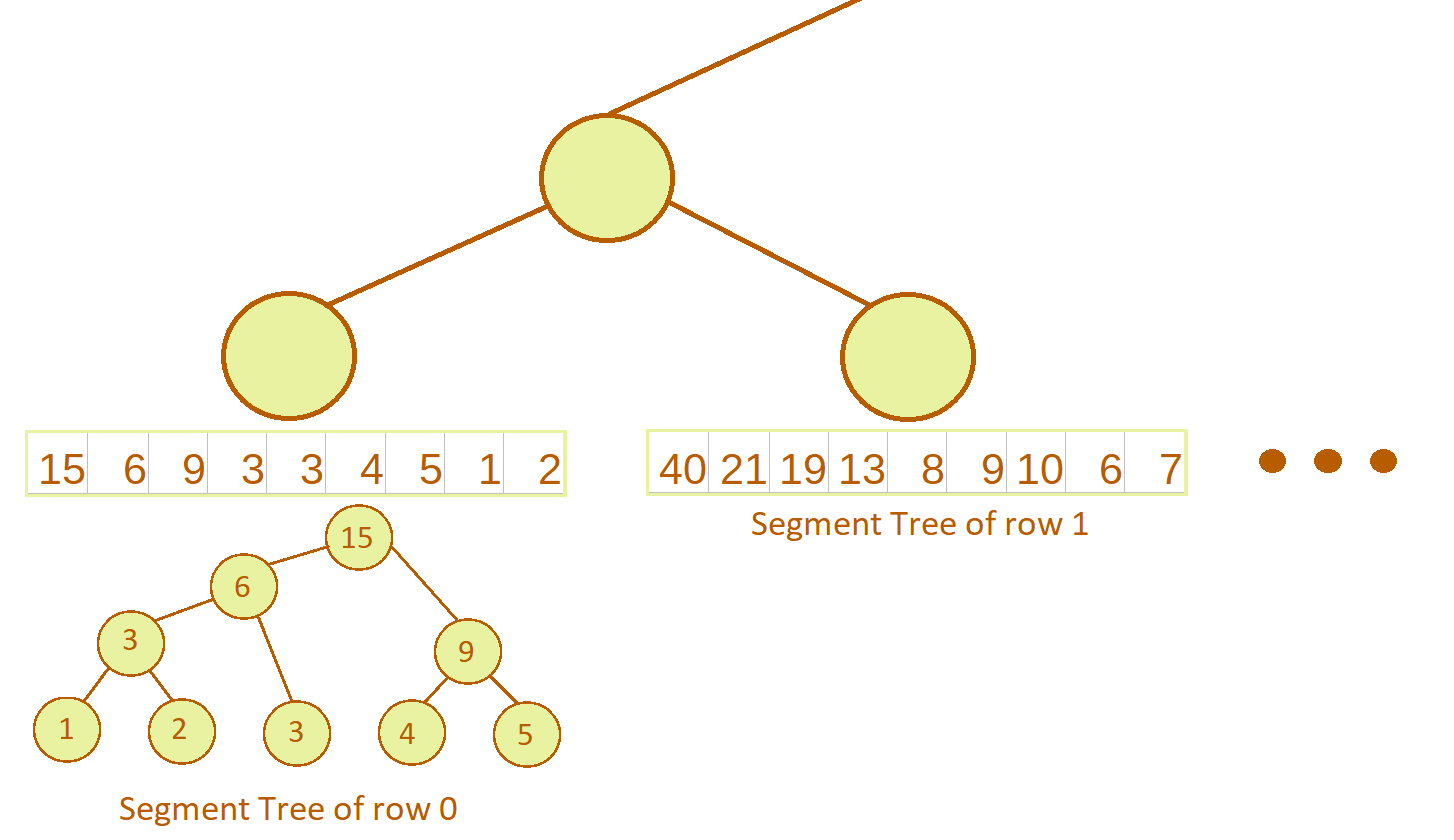
A binary tree can be physically represented as an array. The arrays shown at leaf nodes are the arrays formed from respective segment trees.
A binary tree is stored as an array in following fashion:
- The root node is taken at index 1 of a 1-indexed array, say
ar[1]. - For any node at index
x, its left child is stored at index2xand right child is stored at index2x + 1.
So root will be stored at ar[1], its left child at ar[1] and right child at ar[3] and so on.
- To build an internal node, merge the 2 children segment tree into a single segment tree. Since we are working with sum operation, merge operation is adding corresponding elements of each row. So first element will be
15 + 40 = 55, second will be6 + 21 = 27and so on:
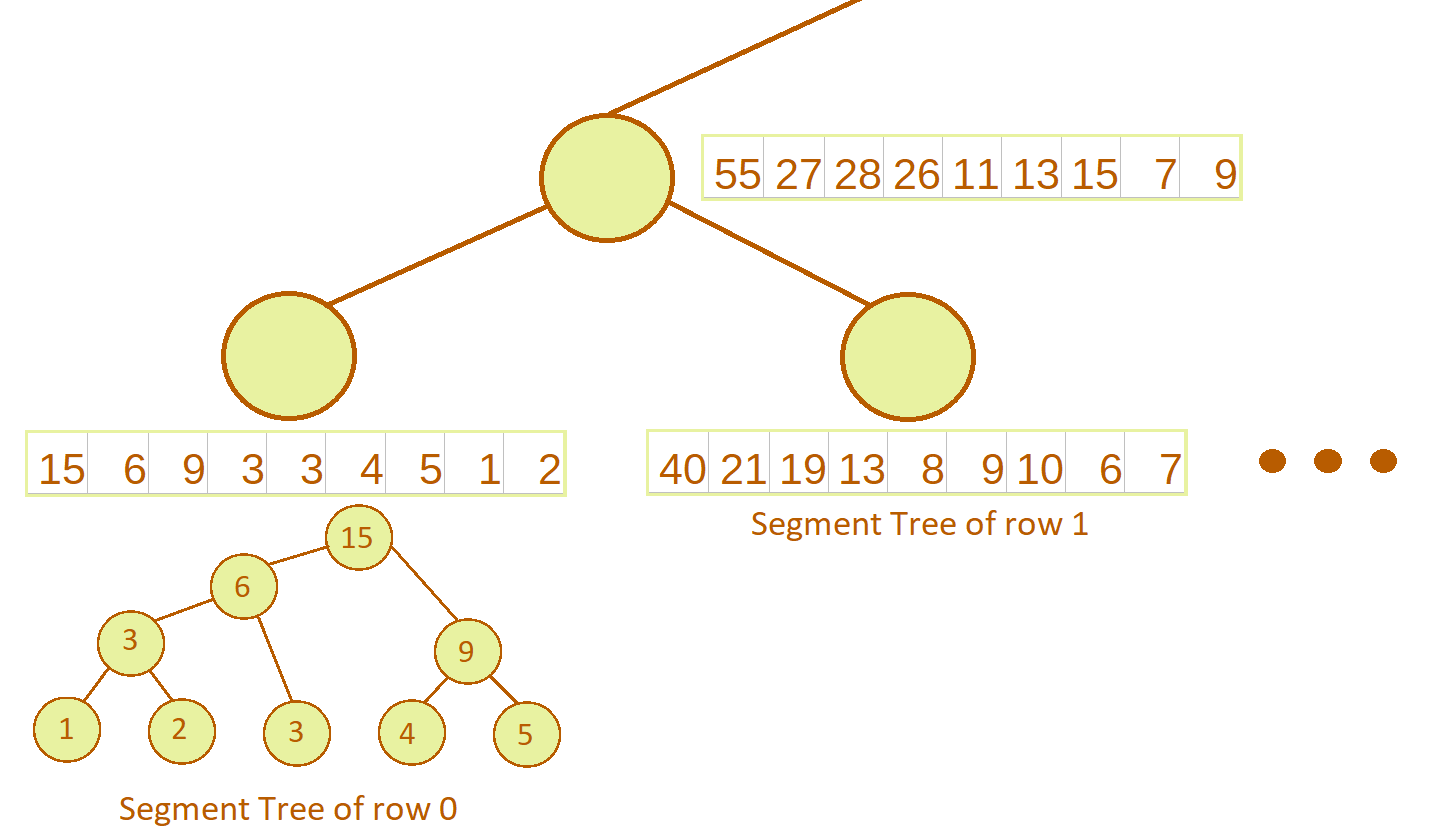
In case of max 2D segment tree, we would take maximum of corresponding elements. In reality, the new segment tree is built by calling every query on both trees and merging those values into new tree, but the method described above has same effect as it is functionally the same thing.
Querying is also modified in same way. First, the 2D segment tree is searched for the 1D segment tree that satisfies the conditions along y-axis, then the 1D segment tree is travered for the node that satisfies conditions along x-axis.
For example, given a query for sub-matrix defined by 2 points (x1, y1), (x2, y2), first 2D segment tree searches for the segment tree bound by left = x1 and right = x2. The resultant segment tree is then searches for the node that satisfies left = y1 and right = y2.
Pseudocode
First part of algorithm is for building a 1D segment tree:
- Building the segment tree.
In this implementation, the tree will be stored directly as an array:
# st is array in which the 1D segment tree is stored.
# length of st must be at-least the no of nodes in ar
# index is index of current node in st. root is st[1].
function build(st, ar, index, L, R):
if L == R:
st[index] = ar[L]
else:
mid = (L + R) / 2
# 2*index will be left child
build(st, array, 2*index, L, mid)
# 2*index + 1 will be right child
build(st, array, 2*index + 1, mid + 1, R)
# finally, add the values from two children into the parent
st[index] = st[2*index] + st[2*index + 1]
# To build the tree for some array ar, call
# build(st, ar, 1, 0, length(ar) - 1)
- Range max query (rMq) operation :
function query(st, index, L, R, start, end):
if start > R or end < L:
# -1 used as null value here
return -1
if L >= start and R <= end:
return st[index]
mid = (L + R) / 2
left = query(st, 2*index, L, mid, start, end)
right = query(st, 2*index + 1, mid + 1, R, start, end)
if left == -1:
return right
if right == -1:
return left
return left + rightSecond part of algorithm is construction of 2D segment tree:
- Building the 2D segment tree :
Since matrices are stored in memory in row major fashion, we will build 2D segment tree along y-axis.
# ST is the matrix representing 2D segment tree, with each row
# being a 1D segment tree.
# mat is the target matrix
# index is used by ST. The segment tree representing complete matrix is ST[1]
# ST must be large enough to hold all 1D segment trees.
# matrix is of size "m x n"
function build2D(ST, mat, index, L, R):
# if at leaf node, build a 1D segment tree
if L == R:
build(ST[index], mat[L], 1, 0, n - 1)
else:
mid = (L + R) / 2
# build left child segment tree
build2D(ST, mat, 2*index, L, mid)
# build right child segment tree
build2D(ST, mat, 2*index + 1, mid + 1, R)
# merge left and right children
for i = 0, i < length(ST[index]), i += 1:
ST[index][i] = ST[2*index][i] + ST[2*index + 1][i]- Querying the 2D segment tree :
# The query function accepts 4 arguments : x1, y1 as top left corner of sub-matrix
# x2, y2 as bottom right corner of sub-matrix.
function query2D(ST, index, L, R, x1, y1, x2, y2):
# in this function, we will operate only on y-axis, so will take x1
# and x2 as limits. query function of 1D segment tree will be used with
# y1 and y2
if L > x2 or R < x1:
return -1;
if L >= x1 and R <= x2:
return query(ST[index], 1, 0, n - 1, y1, y2)
mid = (L + R) / 2
# query left child. Returned value will be integer
left = query2D(ST, 2*index, L, mid, x1, y1, x2, y2)
# query right child. Returned value will be integer
right = query2D(ST, 2*index + 1, mid + 1, R, x1, y1, x2, y2)
if left == -1:
return right
if right == -1:
return left
return left + rightSize of segment tree is 2 x N - 1 where N is the size of array.
So size of 2D segment tree will be (2 x M - 1)(2 x N - 1).
Complexity
The time and space complexity of 2D segment tree are as follows:
$\bf{Space \hspace{1mm }complexity:}\hspace{1mm} O(4 * M * N)$
$\bf{Time\hspace{1mm }complexities:}$
- $\bf{Build:} \hspace{1mm} O(4 * M * N)$
- $\bf{Query:} \hspace{1mm} O(\log_2{M} * \log_2{N})$
Implementations
C++ 11
/*
* Code for 2D segment tree to calculate sum of sub-matrix
*/
#include <iostream>
#include <vector>
class SegmentTree2D{
std::vector<std::vector<int>> st; // to store 2D segment tree
std::vector<std::vector<int>> mat; // to store matrix
int m, n;
public:
SegmentTree2D(std::vector<std::vector<int>> &matrix){
mat = matrix;
m = mat.size();
n = mat[0].size();
// initialize st
st.assign(m + m, std::vector<int> (n + n, 0));
build2D(1, 0, m - 1);
}
void build(std::vector<int> &segTree, std::vector<int> &ar, int index, int L, int R){
if(L == R){
segTree[index] = ar[L];
}
else{
int mid = (L + R) / 2;
// 2*index will be left child
build(segTree, ar, 2*index, L, mid);
// 2*index + 1 will be right child
build(segTree, ar, 2*index + 1, mid + 1, R);
// finally, add the values from two children into the parent
segTree[index] = segTree[2*index] + segTree[2*index + 1];
}
}
int query(std::vector<int> &segTree, int index, int L, int R, int start, int end){
if(start > R || end < L){
// -1 used as null value here
return -1;
}
if (L >= start and R <= end)
return segTree[index];
int mid = (L + R) / 2;
int left = query(segTree, 2*index, L, mid, start, end);
int right = query(segTree, 2*index + 1, mid + 1, R, start, end);
if(left == -1)
return right;
if(right == -1)
return left;
return left + right;
}
void build2D(int index, int L, int R){
// if at leaf node, build a 1D segment tree
if(L == R)
build(st[index], mat[L], 1, 0, n - 1);
else{
int mid = (L + R) / 2;
// build left child segment tree
build2D(2*index, L, mid);
// build right child segment tree
build2D(2*index + 1, mid + 1, R);
// merge left and right children
for(int i = 0; i < st[index].size(); ++i)
st[index][i] = st[2*index][i] + st[2*index + 1][i];
}
}
int query2D(int index, int L, int R, int x1, int y1, int x2, int y2){
if(L > x2 || R < x1)
return -1;
if(L >= x1 and R <= x2)
return query(st[index], 1, 0, n - 1, y1, y2);
int mid = (L + R) / 2;
// query left child. Returned value will be integer
int left = query2D(2*index, L, mid, x1, y1, x2, y2);
// query right child. Returned value will be integer
int right = query2D(2*index + 1, mid + 1, R, x1, y1, x2, y2);
if(left == -1)
return right;
if(right == -1)
return left;
return left + right;
}
// Main query function
int query(int x1, int y1, int x2, int y2){
return query2D(1, 0, m - 1, x1, y1, x2, y2);
}
};
int main(){
std::vector<std::vector<int>> matrix = {std::vector<int>({1, 1, 2, 2}),
std::vector<int>({3, 3, 4, 4}),
std::vector<int>({5, 5, 6, 6}),
std::vector<int>({7, 7, 8, 8})};
SegmentTree2D st(matrix);
std::cout << "Matrix is\n";
for(int i = 0; i < 4; ++i){
for(int j = 0; j < 4; ++j)
std::cout << matrix[i][j] << ' ';
std::cout << '\n';
}
std::cout << "Sum of submatrix ((1, 1), (3, 3)) is " << st.query(1, 1, 3, 3) << '\n';
std::cout << "Sum of row 2 is " << st.query(2, 0, 2, 3) << '\n';
return 0;
}Applications
- Unlike 2D Fenwick Tree, it can process non-onvertible operations like
max(). - The queries can be processed in O(log2mn) time.
- Used for finding sub-matrix sum/product, sub-matrix min/max, sub-matrix xor etc.
References/ Further reading
- Quad tree is generally used in graphics applications. It that can be modified to work as segment tree for sub-matrices. Its time complexity for queries is O(log4mn). Kaidul's article on Quad tree
