
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 30 minutes | Coding time: 12 minutes
Fenwick Tree is used to answer range or interval queries in an array in logarithmic time. Fenwick tree can be generalized to multiple dimensions. 2D Fenwick tree is one such implementation used to answer sub-matrix queries, i.e. queries in 2 dimensions. Fenwick tree is considered a prerequisite to understand 2D Fenwick tree. Like 1D, 2D Fenwick tree also requires the operation to be invertible.
Since Fenwick tree stores prefix sums, 1D Fenwick tree works by processing query(m, n) as query(1, n) - query(1, m - 1). 2D Fenwick tree operates on a matrix, so query is processed differently, but the requirement is still same, i.e. operation must be invertible.
Sub-matrix sum, i.e. sum of all elements of sub-matrix is the most common implementation of 2D Fenwick trees so we will explore this case.
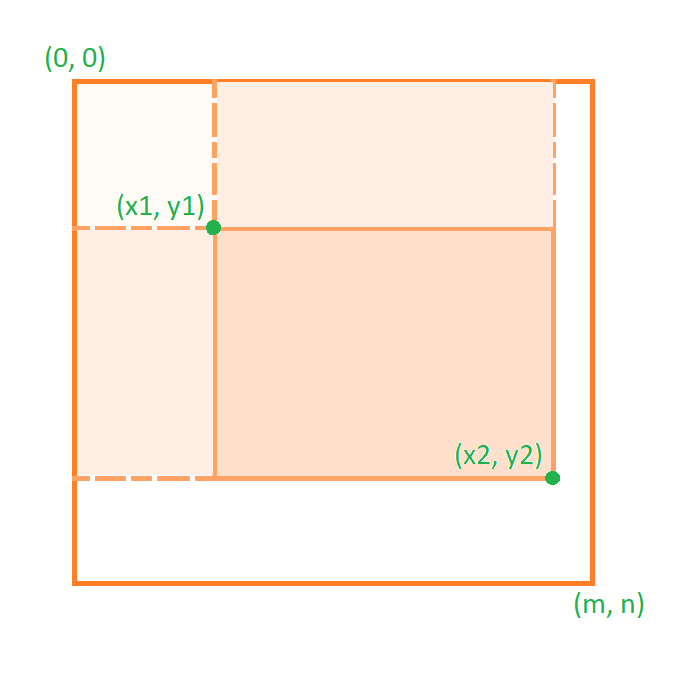
Consider the matrix shown above where we need to answer sum of sub-matrix bound by coordinates (x1, y1) and (x2, y2). It is given by:
sum((x1, y1), (x2, y2)) = sum((0, 0), (x2, y2)) - sum((0, 0), (x1 - 1, y2))
- sum((0, 0), (x2, y1 - 1)) + sum((0, 0), (x1 - 1, y1 - 1))
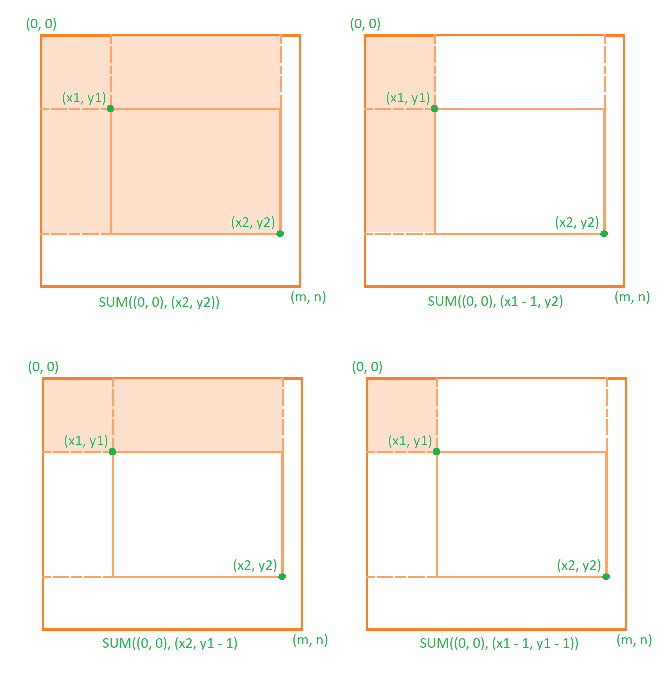
This is direct result of inclusion-exclusion principle .
If we wanted sub-matrix product, the general method would still be same:
prod((x1, y1), (x2, y2)) = prod((0, 0), (x2, y2)) * prod((0, 0), (x1 - 1, y1 - 1))
/ prod((0, 0), (x1 - 1, y2)) / prod((0, 0), (x2, y1 - 1))
Just like Fenwick tree, Least-significant-bit operation is used in 2D Fenwick tree:
int LSB(int i){
return i & (-i);
}
2D Fenwick tree is implemented as a matrix of the same size as target matrix. For a m x n matrix, 2D Fenwick tree is also stored as m x n matrix. 2D Fenwick tree is just a 2D generalization of a Fenwick tree.
Pseudocode
matrix[][]is them x nmatrix upon which 2D Fenwick tree is built.ft[][]is them x nmatrix used to store 2D Fenwick tree.- Least significant bit operation :
function LSB(i): return i & (-i)&isbitwise and. - Updating array at index x : Fenwick Tree at the start is considered to be built upon a zero matrix, so zero is stored at every position. Update is used with every element of
matrix[][]to build up the Fenwick tree. In 2D Fenwick tree, the algorithm for update is just 2-dimensional version of update used in 1D Fenwick tree. Given(x, y)as co-ordinate to be updated:
function update(x, y, value):
while x <= m:
# cannot directly use y since y becomes 0 after single loop
y' = y
while y' <= n:
ft[x][y'] = ft[x][y'] + val
y' = y' + LSB(y')
x = x + LSB(x)- Querying an interval : Algorithm for query is modified similar to update algorithm.
function query(x, y):
sum = 0
while x > 0:
# cannot directly use y since y becomes 0 after single loop
y' = y
while y > 0:
# Process appropriately
sum = sum + ft[x][y]
y' = y' + LSB(y')
x = x + LSB(x)
return sum
function Query(x1, y1, x2, y2):
return (query(x2, y2) - query(x1, y2) - query(x2, y1) + query(x1, y1))Complexity
Space complexity : O(MN)
Worst case time complexities:
- Update : O(log2(MN))
- Query : O(log2(MN))
Where the matrix is of sizeM x N
Implementations
C++ 11
// 2D fenwick tree for sub-matrix sum problem
#include <iostream>
#include <vector>
class FenwickTree{
private:
// Matrix to store the tree
std::vector<std::vector<int>> ft;
public:
// Function to get least significant bit
int LSB(int x){
return x & (-x);
}
int query(int x, int y){
int sum = 0;
for(int x_ = x; x_ > 0; x_ = x_ - LSB(x_)){
for(int y_ = y; y_ > 0; y_ = y_ - LSB(y_)){
sum = sum + ft[x_][y_];
}
}
return sum;
}
int query(int x1, int y1, int x2, int y2){
return (query(x2, y2) - query(x1 - 1, y2) - query(x2, y1 - 1) + query(x1 - 1, y1 - 1));
}
void update(int x, int y, int value){
// also update matrix[x][y] if needed.
for(int x_ = x; x_ < ft.size(); x_ = x_ + LSB(x_)){
for(int y_ = y; y_ < ft[0].size(); y_ = y_ + LSB(y_)){
ft[x_][y_] += value;
}
}
}
FenwickTree(std::vector<std::vector<int>> matrix){
int n = matrix.size();
// matrix must not be empty.
int m = matrix[0].size();
// Initialize matrix ft
ft.assign(m + 1, std::vector<int> (n + 1, 0));
for(int i = 0; i < m; ++i){
for(int j = 0; j < n; ++j)
update(i + 1, j + 1, matrix[i][j]);
}
}
};
int main(){
//sample code
std::vector<std::vector<int>> matrix = {std::vector<int>({1, 1, 2, 2}),
std::vector<int>({3, 3, 4, 4}),
std::vector<int>({5, 5, 6, 6}),
std::vector<int>({7, 7, 8, 8})};
FenwickTree ft(matrix);
std::cout << "Matrix is\n";
for(int i = 0; i < 4; ++i){
for(int j = 0; j < 4; ++j)
std::cout << matrix[i][j] << ' ';
std::cout << '\n';
}
std::cout << '\n';
std::cout << "Sum of submatrix ((2, 2), (4, 4)) is " << ft.query(2, 2, 4, 4) << '\n';
std::cout << "After changing 3 at (2, 2) to 10, matrix is\n";
matrix[2 - 1][2 - 1] += 7;
ft.update(2, 2, 7);
std::cout << "Matrix is\n";
for(int i = 0; i < 4; ++i){
for(int j = 0; j < 4; ++j)
std::cout << matrix[i][j] << ' ';
std::cout << '\n';
}
std::cout << '\n';
std::cout << "Sum of submatrix ((2, 2), (4, 4)) is " << ft.query(2, 2, 4, 4) << '\n';
return 0;
}Applications
- Is much more space efficient than 2D Segment tree or Quad tree.
- The queries can be processed in O(log2mn) time.
- Used for finding sub-matrix sum/product etc.
- Cannot be used for sub-matrix min/max.
References/ Further reading
- Try 3D Fenwick tree as an exercise.
- Paper by Pushkar Mishra.
- Also read about quad tree which is used for similar applications. Kaidul's article on Quad tree
