Bresenham’s Circle Drawing Algorithm

Reading time: 25 minutes | Coding time: 15 minutes

Bresenham’s Circle Drawing Algorithm is a circle drawing algorithm that selects the nearest pixel position to complete the arc. The unique part of this algorithm is that is uses only integer arithmetic which makes it, significantly, faster than other algorithms using floating point arithmetic in classical processors.

Example:

Algorithm

As per Eight way symmetry property of circle, circle can be divided into 8 octants each of 45-degrees.

The Algorithm calculate the location of pixels in the first octant of 45 degrees and extends it to the other 7 octants. For every pixel (x, y), the algorithm draw a pixel in each of the 8 octants of the circle as shown below :

Assumption : Center of Cirle is Origin.

Following image illustrates the 8 octants with corresponding pixel:

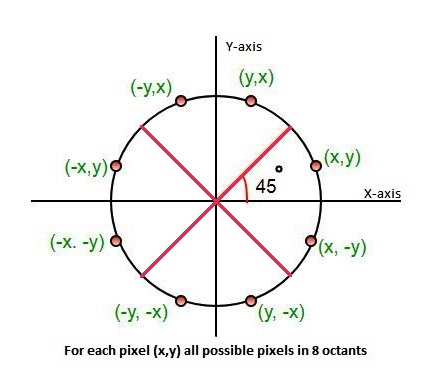
Point (x, y) is in the first octant and is on the circle.

To calculate the next pixel location, can be either:

• N (x+1, y)
• S (x+1, y-1)

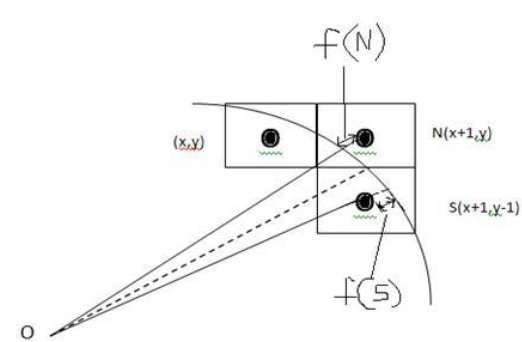
It is decided by using the decision parameter d as:

• If d <= 0, then N(x+1, y) is to be chosen as next pixel.
• If d > 0, then S(x+1, y-1) is to be chosen as the next pixel.

Pseudocode

Draw the circle for a given radius ‘r’ and centre (xc, yc) starting from (0, r) and move in first quadrant till x=y (i.e. 45 degree) ,first octant.

Initial conditions :

• x = 0
• y = r
• d = 3 - (2 * r)

Steps:

• Step 1 : Set initial values of (xc, yc) and (x, y)
• Step 2 : Calculate decision parameter d to d = 3 – (2 * r).
• Step 3 : call displayBresenhmCircle(int xc, int yc, int x, int y) method to display initial(0,r) point.
• Step 4 : Repeat steps 5 to 8 until x < = y
• Step 5 : Increment value of x.
• Step 6 : If d < 0, set d = d + (4*x) + 6
• Step 7 : Else, set d = d + 4 * (x – y) + 10 and decrement y by 1.
• Step 8 : call displayBresenhmCircle(int xc, int yc, int x, int y) method.
• Step 9 : Exit.

Implementation

        #include <iostream>
        // Part of Cosmos by OpenGenus Foundation
        class BresenhamCircle
        {
        public:
            BresenhamCircle(int radius_) : radius_(radius_)
            {
            }
            void getRadiusCenter();
            void drawBresenhamCircle();
            void displayBresenhmCircle(int xc_,int yc_, int x, int y);
        private:
            int radius_;
            int xc_;
            int yc_;
        };

        void BresenhamCircle::drawBresenhamCircle() {
            int x = 0, y = radius_;
            int decesionParameter = 3 - 2 * radius_;
            displayBresenhmCircle(xc_, yc_, x, y);
            while (y >= x)
            {
                x++;
                if (decesionParameter > 0)
                {
                    y--;
                    decesionParameter = decesionParameter + 4 * (x - y) + 10;
                }
                else
                    decesionParameter = decesionParameter + 4 * x + 6;
                displayBresenhmCircle(xc_, yc_, x, y); //displaying all the Eight Pixels of (x,y)
                delay(30);
            }
        }
        void BresenhamCircle::getRadiusCenter() {
            std::cout << "\nEnter Radius of the Circle : ";
            std::cin >> radius_;
            std::cout << "\nEnter X-Coordinate of Center of Circle : ";
            std::cin >> xc_;
            std::cout << "\nEnter Y-Coordinate of Center of Circle : ";
            std::cin >> yc_;
        }
        void BresenhamCircle::displayBresenhmCircle(int xc_,int yc_, int x, int y) {
            //displaying all 8 coordinates of(x,y) residing in 8-octants
            putpixel(xc_+x, yc_+y, WHITE);
            putpixel(xc_-x, yc_+y, WHITE);
            putpixel(xc_+x, yc_-y, WHITE);
            putpixel(xc_-x, yc_-y, WHITE);
            putpixel(xc_+y, yc_+x, WHITE);
            putpixel(xc_-y, yc_+x, WHITE);
            putpixel(xc_+y, yc_-x, WHITE);
            putpixel(xc_-y, yc_-x, WHITE);
        }
        int main()
        {
            int gd = DETECT, gm;
            initgraph(&gd, &gm, NULL);
            BresenhamCircle b(0);
            //accepting the radius and the centre coordinates of the circle
            b.getRadiusCenter();
            /*
             * selecting the nearest pixel and displaying all the corresponding
             * points of the nearest pixel point lying in 8-octants.
             *
             */
            b.drawBresenhamCircle();
            delay(200);
            closegraph();
        }
        

Complexity

The time and space complexity of Bresenham’s Circle Drawing Algorithm are:

• Worst case time complexity: Θ(n)
• Average case time complexity: Θ(n)
• Best case time complexity: Θ(n)
• Space complexity: Θ(1)

where N is radius of circle.

Further reading

• Bresenham Line Drawing Algorithm