Theoretically, a queue is considered as a sequential collection of entities which can be modified by the addition of entities at one end of the sequence known as the rear end and removal from the other end of the sequence known as the front end of the queue. It is an abstract data type in which the data is arranged in a linear fashion.

We have explored the types of queue along with its implementations.

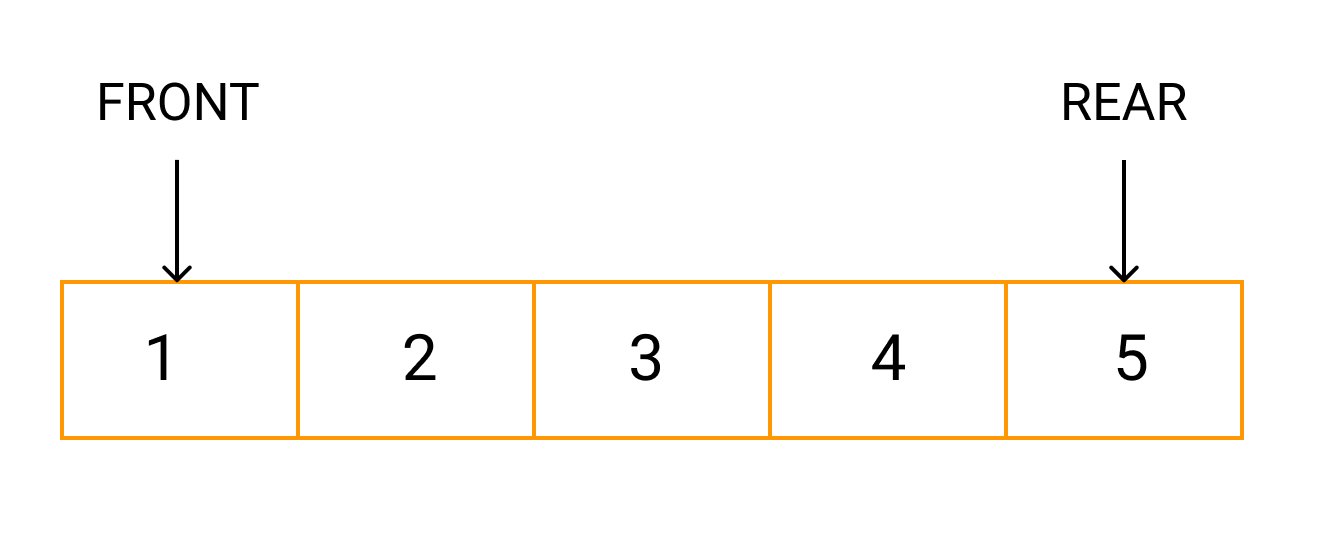
All the operations that are performed in the queue are performed primarily on a first come first serve basis.The job which is enqueued first gets processed first. This is technically referred to as First-In-First-Out(FIFO) principle.

Some commonly seen real life examples of queue are:

• A queue of individuals at ticket-window: The one who comes first gets the ticket first. The one who comes last gets the tickets in last.
• Vehicles on toll-tax bridge: The vehicle that comes first to the booth leaves first and the vehicle that comes last leaves last.

Types Of Queues

On the premise of the arrangement of nodes and their priorities , we have the following types of queues:

1. Linear Queue
2. Circular Queue
3. Priority Queue
4. Dequeue (Double Ended Queue)

Linear Queue

A linear or simple queue is a queue where insertion takes place at the front of the queue and deletion takes place at the end of the queue.These may be represented in the computer memory by means of linear arrays or linked list.

It has three components:

• A container of things that contains elements of queue.
• A pointer front that points to the first/primary item of the queue.
• A pointer rear that points to the last item of the queue.

Implementation of the Linear Queue

All types of queues can be implemented by using either of the following ways -

1. Arrays
2. Linked List
   Let us discuss both the approaches here for linear queues -

Implementation using array

For implementing a queue using array, we declare array, front and rear as global variables and initialize them within the class constructor as shown below

Sample source code-

class Queue 
{ 
    int front, rear; //to point to front and rear of the queue 
    int  capacity; //to declare maximum number of the elements the queue will hold
    int array[]; //global array for the queue
       
    public Queue(int capacity) { 
         this.capacity = capacity; 
         front = 0;  
         rear = capacity - 1; 
         array = new int[this.capacity];   //variables initialized in the constructor.
            
    }
}

Implementation using Linked List-

In order to implement a queue using a linked list , we use two nested classes. Pointers front and rear are used to keep track of the front and rear of the queue. In addition to them , we declare a linked list node to store the elements of the queue as shown below-

Sample Source Code-

class Node
{                                 // A linked list (LL) node to store a queue data
   int key;          //store data
   Node next;        //store address of the next node of the queue
 
public Node(int key)           // constructor to initialize and create the new node
   {
       this.key = key;
       this.next = null;
   }
}
 
class Queue
{                                         // A class to represent a queue
  Node front, rear;     //front stores the front node and rear stores the rear node

   public Queue()
   {
       this.front = this.rear = null;    //initialises front and rear 
   }

Circular Queue

A circular queue is a linear data structure which also behaves like a first-in-first-out(FIFO) type data structure but in place of starting and ending at two different locations , it comes again at the first position after crossing the last one.

Need of circular queue

In a Linear queue, once the queue is full, it is not possible to insert more elements. Even if we dequeue the queue to remove some of the elements, new elements cannot be inserted until the queue is reset. This happens because removing is done from the front of the queue , the front pointer is decremented but the rear pointer stays at the end.In this scenario , the only solution is to begin afresh. To overcome this drawback , we use circular queues.

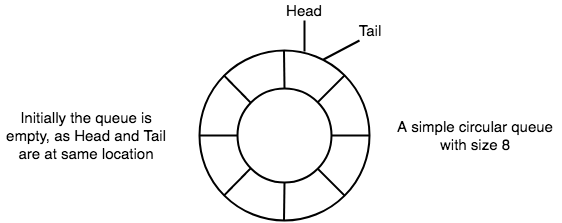
Let us have a quick look at some of the basic points about circular queue-

• In case of circular queue , the head pointer points to the head/front of the queue and the tail pointer points to the tail/rear of the queue.
• Initially , when the queue is empty , both the pointers(head and tail) point to the same location.
• New data is always added to the tail of the queue and once the data is added, the tail pointer is updated to point to the next available location.

Implementation of the Circular Queue

All types of queues can be implemented by using either of the following ways -

1. Arrays
2. Linked List

Let us discuss both the approaches here for circular queues -

Implementation using array

For implementing a queue using array, we declare an array, front and rear as global variables and initialize them in the class constructor as shown below

Sample source code-

class CircularQueue {

     int[] queue; //Array to hold elements
     int maxSize; //Maximum size of the queue

     int rear;//rear position of the queue
     int front; //front position of queue       

    public CircularQueue(int maxSize) {
        this.maxSize = maxSize;     //intialise global variables
        queue = new int[this.maxSize]; //to their respective values
        front = -1;
        rear = -1;
    }
}

Implementation using Linked List-

In order to implement a queue using a linked list , we use two nested classes. Pointers front and rear are used to keep track of the front and rear of the queue. In addition to them , we declare a linked list node to store the elements of the queue as shown below-

Sample Source Code-

class CircularQueue {
    static class Node  //structure of node
      {  
         int data;  //to hold data
         Node  link;  //to point to next node in sequence
      }  
    static class Queue  
      {  
        Node  front,  rear; //pointers to point to head and tail
        public Queue()  //class contructor to initialise values to null
        {
          this.front=null;
          this.rear=null;
        }
      }
}

Priority Queue

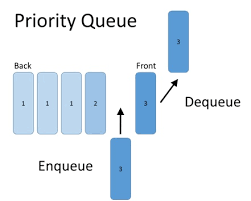
A Priority Queue is employed when the items are supposed to be processed on the basis of assigned priority.Priority Queue is an extension of queue with following properties.

• Every item incorporates a priority associated with it.
• An element having higher priority is removed before an element having lower priority.
• In case two elements have the same priority, they are processed in line with their order in the queue.

Implementation of the Priority Queue

Priority queues can be implemented using an array, a linked list, a heap or a binary search tree.

Time Complexities for various data structures

Data Structure	peek()	insert()	delete()
Linked List	O(1)	O(n)	O(1)
Binary Heap	O(1)	O(logn)	O(logn)
Binary Search Tree	O(1)	O(logn)	O(logn)

Among these data structures, heap data structure provides an efficient and easy way for implementation of priority queues , so let us try to implement a max priority queue using max heap.

class MaxPriorityQueue {
  public static int hs = 0;  //to store heap size
  public static int as = 20; //declare queue size
  public static int INF = 100000;

  //function to get right child of a node
  public static int getRC(int A[], int index) {
    if((((2*index)+1) < A.length && (index >= 1)))
      return (2*index)+1;
    return -1;
  }

  //function to get left child of a node
  public static int getLC(int A[], int index) {
      if(((2*index) < A.length && (index >= 1)))
          return 2*index;
      return -1;
  }
  //function to create max heap
  public static void maxHeapify(int A[], int index) {
    int leftCIndex = getLC(A, index);  //left child index
    int rightCIndex = getRC(A, index); //right child index

    // finding largest among index, left child and right child
    int l = index;

    if ((leftCIndex <= hs) && (leftCIndex>0)) {
      if (A[leftCIndex] > A[l]) {
        l = leftCIndex;
      }
    }

    if ((rightCIndex <= hs && (rightCIndex>0))) {
      if (A[rightCIndex] > A[l]) {
        l = rightCIndex;
      }
    }

    // largest is not the node, node is not a heap
    if (l != index) {
      int temp;
      temp = A[l];    //swapping them
      A[l] = A[index];
      A[index] = temp;
      maxHeapify(A, l);
    }
  }

  public static void buildHeap(int A[]) {
    for(int i=hs/2; i>=1; i--) {
      maxHeapify(A, i);
    }
  }
  
  public static void main(String[] args) {
    int Q[] = new int[as];
    buildHeap(Q);
  }
}

Dequeue (Doubly Ended Queue)

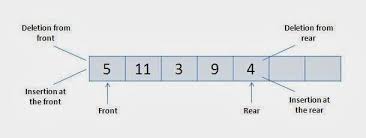
Dequeue or Double Ended Queue is a generalized form of Queue data structure that permits insertion and deletion at both ends.
There are two types of dequeues -

1. Input Restricted DeQueue
2. Output Restricted DeQueue

In Input Restricted DeQueue , insertion is restricted to be done only from REAR, but deletion may be done from both FRONT and REAR.
In Output Restricted DeQueue, deletion is restricted to be done only from FRONT, but insertion may be done from both FRONT and REAR.

Implementation of the Dequeue

All types of queues can be implemented by using either of the following ways -

1. Arrays
2. Linked List

Let us discuss both the approaches here for dequeues -

Implementation using array

For implementing a dequeue using array, we declare an array, front and rear as global variables and initialize them in the class constructor as shown below

Sample source code-

class DeQueue {
     public int front; //to point to front of queue
     public int rear;  //to point to rear of queue
     int dequeue[];  //to store elements of queue
     
     public DeQueue(int size) //constructor to intialise variables.
     {
       front=0;
       rear=-1;
       this.dequeue = new int[size];
     }
     
}

Implementation using Linked List-

In order to implement a queue using a linked list , we use two nested classes. Pointers front and rear are used to keep track of the front and rear of the queue. In addition to them , we declare a doubly linked list node to store the elements of the queue as shown below-

Sample Source Code-

class Node
{
 public int data;       //to store data
 public Node prev;      //to store address of previous node
 public Node next;      //to store address of next node
 public Node(int data)  //to intialise variables and create a Node object
 {
   this.data=data;
   this.prev=null;
   this.next=null;
 }
}
class Dequeue
{
 Node  front,  rear; //pointers to point to head and tail
        public Dequeue()  //class contructor to initialise values to null
        {
          this.front=null;
          this.rear=null;
        }
}

Applications of Queue

Queues support the principle of first-in-first-out and hence find it's use in a variety of scenarios.Mainly, queues are used whenever we need to manage a collection of entities such that the order of them being enqueued is sustained.

1. Serving requests on one shared resource,sort of a printer, CPU task scheduling, etc.
2. Call Center phone systems use Queues to manage people calling them until a service representative is free.
3. Handling of interrupts in real-time computer systems.
4. Graph Traversals

With this article at OpenGenus, you must be able to understand and implement different types of queues. Till then, go ahead and use it in your programs. Happy Coding!