
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
A queue is a linear data structure that supports First-In-First-Out operation.In this article, we'll be discussing following algorithms and problems that can be solved directly by using queues:
Algorithms
- CPU Scheduling(First-Come-First-Serve)
- Breadth First Search Traversal
- Level Order Traversal of a tree
- Edmonds Karp Algorithm
- Dinic's Algorithm
- Fibonacci Heap
Problems
- Maximum for each continuous subarray
- Maximum amount that can be collected by selling spots
- Odd even level difference
So, let us start with the case of FCFS CPU Scheduling algorithm -
CPU Scheduling Algorithm(FCFS)
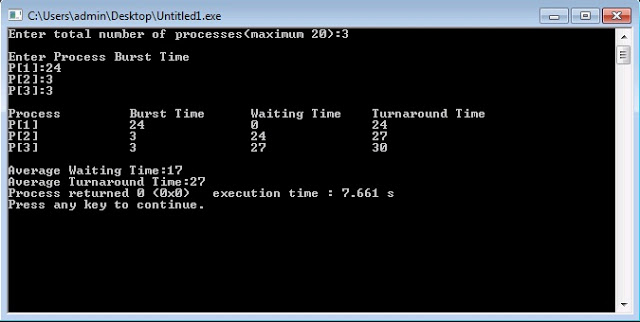
CPU Page replacement algorithm - FCFS(First-Come-First-Serve) is needed to decide which page needs to be replaced in the memory when a new page comes in. In this algorithm, the operating system keeps track of all pages in the memory in a queue. When a page needs to be replaced, the page at the front of the queue is selected for removal(queue follows FIFO,hence element at the front will be the oldest).
Algorithm -
- Start traversing the pages.
- If a frame holds lesser pages than it's maximum capacity.
- Insert pages into the set one by one until the size of set reaches capacity or all page requests are processed.
- Update the pages in the queue to perform FIFO.
- Increment page fault
- Else
If the current page is present in set, do nothing.
Else
1. Remove the first page from the queue.
2. Replace it with the current page in the string and store current page in the queue.
3. Increment page faults.
- Return page faults.
Solution
For the sake of simplicity , let us use the queue interface so as to avoid the manual implementation part.
static int FIFO(int pages[], int n, int capacity)
{
//To maintain record of //existing pages
HashSet<Integer> s = new HashSet<>(capacity);
Queue<Integer> indexes = new LinkedList<>() ; //to implement FIFO
int pf = 0;
for (int i=0; i<n; i++) // Start from initial page
{
if (s.size() < capacity) // Check if more pages can be held in set
{
if (!s.contains(pages[i]))
{
s.add(pages[i]); // Insert it into set if not present already
pf++; //Increment page faults
indexes.add(pages[i]); // Add the current page into the queue
}
}
else // Now , since no more pages can be held
{ //in that set , hence , FIFO
if (!s.contains(pages[i])) // Check if current page is not
{ //already present in set
int val = indexes.peek(); //Dequeue the first page
indexes.poll(); //from the queue
s.remove(val); // Remove the indexes page
s.add(pages[i]); // insert the current page
indexes.add(pages[i]); // Add the current page to the queue
pf++; // Increment page faults
}
}
}
return pf;
}
To-Do-
We can also find the number of page hits. one only needs to maintain a separate count. If the current page is already in the memory then that is counted as Page-hit. Try doing this yourself !
Breadth First Search (BFS) Algorithm
Breadth first search is a graph traversal algorithm that starts traversing the graph from root node and visits all the neighbouring nodes. Then, it selects the nearest node and visits all the unvisited nodes. This process is carried on recursively until all nodes have been visited.
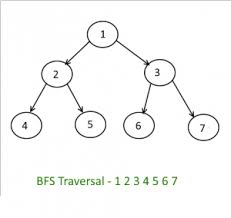
In this algorithm , we maintain a linear queue of the nodes to maintain the status of nodes in ready state. Following is the detailed BFS Algorithm-
Algorithm
Step 1: Set the status=1(ready state) for each node in G.
Step 2: Insert the first node A and set its status = 2(waiting state).
Step 3: Now, repeat steps 4 and 5 until queue is empty
Step 4: Dequeue a node, process it and set it's status = 3(processed state).
Step 5: Insert all the neighbours of N that are in the ready state(staus=1) and set their status = 2(waiting state)
(END OF LOOP)
Step 6: EXIT
Solution
private LinkedList<Integer> al[]; //Adjacency List for traversal
public int v=5; //number of vertex in graph
void traverse(int s) //s is the starting vertex
{
//initially consider all the vertices as unvisited
boolean visit[] = new boolean[v];
LinkedList<Integer> q = new LinkedList<Integer>();//for traversal
visit[s]=true; // Mark the current node as visited
q.add(s); //add starting vertex to queue
while (q.size() != 0)
{
s = q.poll(); // Remove a vertex from queue
System.out.print(s+" ");
Iterator<Integer> i = al[s].listIterator(); //to iterate
while (i.hasNext())
{
int n = i.next(); //neighbouring vertex of dequeued vertex
if (!visit[n])
{
visit[n] = true; //process them
q.add(n); //store in queue
}
}
}
}
This implementation uses adjacency list representation of graphs.
To-Do
We can also traverse a graph by means of adjacency matrix. Try doing this yourself!
Level Order Traversal of a tree
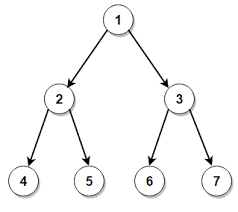
Level Order Traversal is one of the most used algorithms while dealing problems on trees. In level order traversal, we iterate through all levels of the tree one by one , traversing all the nodes at a specific level in a linear fashion.
Now , there can be two ways of implementing this. A naive approach is to recursively call two functions. One of them traverses all nodes at a given level and the other determines the height of the tree and traverse them level-wise.
However, the expected time-complexity of this method in worst-case is O(n * n). This can be further optimised to linear time complexity by using linear queues.
Let us first have a look at the detailed algorithm we are talking about and then, we'll move on to the implementation part!!!
Algorithm
- Initialise a linear queue, q and push root of the tree to it's front.
- Repeat steps 3-4 until queue is not empty.
- Remove the node at the front of the queue and process it.
- Push the children of the node to the queue.
Now, let's move on to the implementation part. Before moving on to the solution , try doing this yourself
void print(Node root)
{
if(root==null)
{
return; //in case root is null , there is no node to traverse.
}
Queue<Node> q = new LinkedList<Node>(); //queue to hold nodes
q.add(root); //add root to it
while(!q.isEmpty()) //loop till queue is empty
{
int size = q.size(); //variable to store size of queue
for(int i=0;i<size;i++)
{
Node temp = q.remove(); //dequeue the first node
System.out.print(temp.data+" "); //print data
if(temp.left!=null) //Push it's children to queue
q.add(temp.left);
if(temp.right!=null)
q.add(temp.right);
}
}
}
To-Do
We can also find the depth of each nodes iteratively using this method.All you need to do is to maintain a separate variable to track changes in levels.Try implementing this yourself!!
Edmonds Karp Algorithm
This algorithm is used for determining the maximum flow in a flow network.
In graph theory, a flow network is basically a directed graph that connects a Source(S), a Sink(T) and other nodes with edges.Every edge has it's own capacity which is the maximum limit of flow through this edge.
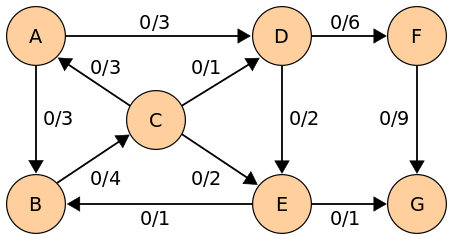
Edmonds-Karp algorithm is an extension to the Ford–Fulkerson algorithm but it is more efficient.
Time Complexity - O(V * E * E)
The only difference between Edmonds-Karp algorithm and Ford-Fulkerson is that it determines the next augmenting path using breadth-first search (bfs). In other words, this algorithm always chooses the shortest possible path for finding the maximum flow.
Implementation
static final int V = 6;
//for breadth first traversal
boolean bfs(int graph[][], int s, int t, int parent[])
{
boolean check[] = new boolean[V]; // array to check status
for(int i=0; i<V; ++i)
check[i]=false; //mark all nodes as unvisited
LinkedList<Integer> q = new LinkedList<Integer>();
q.add(s); //push start/source vertex to queue
check[s] = true; //mark source node as traversed
parent[s]=-1;
while (q.size()!=0)
{
int u = q.poll(); //remove first vertex from queue
for (int v=0; v<V; v++)
{
if (check[v]==false && graph[u][v] > 0)
{
q.add(v);
parent[v] = u;
check[v] = true;
}
}
}
return (check[t] == true);//return true once we reach sink
}
// Implement fold fulerson algo
int ff(int graph[][], int s, int t)
{
int u, v;
int Graph[][] = new int[V][V];//Create a residual graph and
for (u = 0; u < V; u++) //fill it with same capacities
for (v = 0; v < V; v++) //as original graph
Graph[u][v] = graph[u][v];
int parent[] = new int[V]; //to store path
int max_flow = 0; // Initally, flow is not present
while (bfs(Graph, s, t, parent)) //if a path exists from source to sink
{
int pathFlow = Integer.MAX_VALUE;//to find minimum residual
for (v=t; v!=s; v=parent[v]) //capacity of edges
{
u = parent[v];
pathFlow = Math.min(pathFlow, Graph[u][v]);
}
for (v=t; v != s; v=parent[v])
{
u = parent[v];
Graph[u][v] -= pathFlow;
Graph[v][u] += pathFlow;
}
max_flow += pathFlow; //add to overall flow
}
return max_flow;
}
Dinic's Algorithm
Dinic's Algorithm is another algorithm based on Fold-Fulkerson algorithm which computes the maximum flow in a flow network.
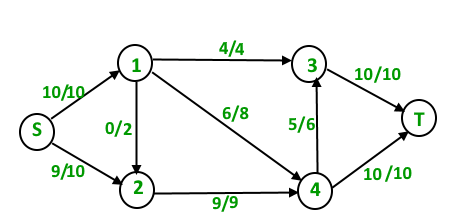
It is more efficient than both Fold-Fulkerson and Edmonds-Karp algorithm.
Time Complexity - O(E * V * V)
Let us have a quick look at the detailed algorithm.
Algorithm
- Create a residual graph G and fill it with the same capacities as original graph.
- Do BFS of G to construct a level graph and check if a greater flow is found.
a) If more flow is not possible, then return.
b) Send multiple flows in G using level graph until blocking flow is reached.
Implementation
static boolean dinicBfs(List<Edge>[] graph, int src, int dest, int[] dist) {
Arrays.fill(dist, -1);
dist[src] = 0;
int[] Q = new int[graph.length];
int sizeQ = 0;
Q[sizeQ++] = src;
for (int i = 0; i < sizeQ; i++) {
int u = Q[i];
for (Edge e : graph[u]) {
if (dist[e.t] < 0 && e.f < e.cap) {
dist[e.t] = dist[u] + 1;
Q[sizeQ++] = e.t;
}
}
}
return dist[dest] >= 0;
}
static int dinicDfs(List<Edge>[] graph, int[] ptr, int[] dist, int dest, int u, int f) {
if (u == dest)
return f;
for (; ptr[u] < graph[u].size(); ++ptr[u]) {
Edge e = graph[u].get(ptr[u]);
if (dist[e.t] == dist[u] + 1 && e.f < e.cap) {
int df = dinicDfs(graph, ptr, dist, dest, e.t, Math.min(f, e.cap - e.f));
if (df > 0) {
e.f += df;
graph[e.t].get(e.rev).f -= df;
return df;
}
}
}
return 0;
}
public static int maxFlow(List<Edge>[] graph, int src, int dest) {
int flow = 0;
int[] dist = new int[graph.length];
while (dinicBfs(graph, src, dest, dist)) {
int[] ptr = new int[graph.length];
while (true) {
int df = dinicDfs(graph, ptr, dist, dest, src, Integer.MAX_VALUE);
if (df == 0)
break;
flow += df;
}
}
return flow;
}
Fibonacci Heap
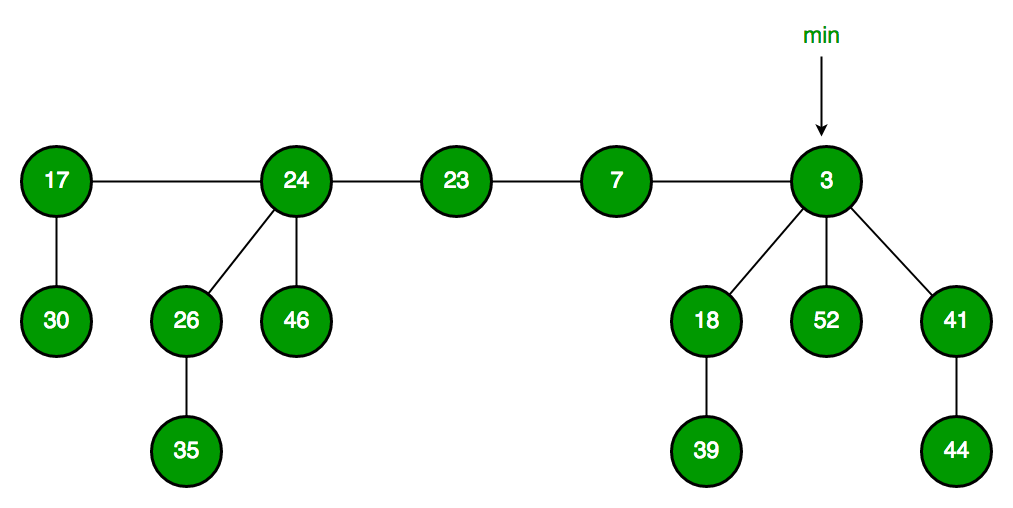
A fibonacci heap is another implementation of heaps that have min-heap or max-heap property. It uses fibonacci numbers and is used to implement priority queues in efficient running time.
Amortized time complexities of Fibonacci Heap
| Operation | Time Complexity |
|---|---|
| Find minimum element | Θ(1) |
| Delete minimum element | O(Log n) |
| Insert element | Θ(1) |
| Decrease key | Θ(1) |
| Merge | Θ(1) |
Implementation
class FibNode
{ //structure of node
FibNode child, left, right, parent;
int element;
public FibNode(int element) //constructor for initialising
{
this.right = this;
this.left = this;
this.element = element;
}
}
class FibHeap
{
private FibNode root; //root node
private int count;
public FibHeap() //constructor for initialisation
{
root = null;
count = 0;
}
public boolean isEmpty() //if heap is empty or not
{
return root == null;
}
public void clear() //clear heap contents
{
root = null;
count = 0;
}
public void insert(int data) //to insert an element
{
FibNode node = new FibNode(data); //new node to insert
node.element = data;
if (root != null)
{
node.left = root;
node.right = root.right;
root.right = node;
node.right.left = node;
if (data < root.element)
root = node;
}
else
root = node;
count++;
}
}
Maximum for each continuous subarray
Given an array and an integer K, find the maximum value for each and every continuous subarray of size k.
Examples :
Input: arr[] = {1, 2, 3, 1, 4, 5, 2, 3}, K = 4
Output: 3 4 5 5 5
There can be multiple approaches for this question , let us have a quick look at each of them and analyse their time complexitites.
Approach 1: Naive Approach
We can run two loops. In the outer loop,we will generate all subarrays of size K and in the inner one, we will find the maximum of the current subarray.
Time Complexity- O(N * K)
Approach 2-: Binary Search Tree
- Pick first k elements and create a Self-Balancing Binary Search Tree (BST).
- Run a loop from i = 0 to n – k
- Print the maximum element from the BST.
- Delete arr[i] from BST and insert arr[i+k] into the BST.
Time Complexity- O(N * Log k)
Approach 3: Dequeue
We use the concept of sliding window technique here and create a Dequeue, Q of size k to store elements of current window only in such a way that it is greater than all other elements on the left side of itself.in this way, Q is always sorted and the maximum element can be retrieved immediately from the front of the queue.
Time Complexity: O(n)
Solution-
static void printMax(int arr[], int n, int k)
{
// Dequeue to store indexes of elements in every window
Deque<Integer> Q = new LinkedList<Integer>();
int i;
//Process first k elements
for (i = 0; i < k; ++i)
{
// delete smaller elements of previous window
while (!Q.isEmpty() && arr[i] >= arr[Q.peekLast()])
Q.removeLast();
Q.addLast(i); // Add new element
}
// Process other elements
for (; i < n; ++i)
{
System.out.print(arr[Q.peek()] + " "); //greatest element
// delete elements of previous window
while ((!Q.isEmpty()) && Q.peek() <= i - k)
Q.removeFirst();
while ((!Q.isEmpty()) && arr[i] >= arr[Q.peekLast()])
Q.removeLast();
Q.addLast(i); // Insert current element at the rear of Qi
}
System.out.print(arr[Q.peek()]); // Print greatest element
}
Maximum amount that can be collected by selling spots
Given an integer N and an array spots[] where N is the number of customers standing to secure their spots for the coming event and seat[i] is the number of vacant spots in the ith row. The task is to find the maximum amount the owner can get by selling them. Price of a spot is equal to the maximum number of empty spots among all the rows.
Example:
Input: seats[] = {1, 2, 4}, N = 3
Output: 9
This problem can be solved by using a priority queue to record the count of empty spots for every row and print the greatest among them.
Algorithm -
- Initialise a priority queue q.
- Traverse the input array and insert all the elements in the queue.
- Initialize two variables sold and ans to store the number of sold tickets and total amount collected.
- Now, while sold < N and q.top() > 0 , delete the top element from the queue and add top element of the queue to ans.
- Now, decrement that top value and insert it again to the queue.
- Repeat these steps until all the spots have been sold.
- Print ans.
Solution -
int M=3; //size of input array
static int s[]={1,2,4}; //input array
public static int Amount(int M, int N)
{
// Priority queue to store count of empty spots
PriorityQueue<Integer> q =
new PriorityQueue<Integer>(Collections.reverseOrder());
for (int i = 0; i < M; i++)
{
q.add(s[i]); // Insert every element to q
}
int sold = 0; // To store the total number of spots sold
int ans = 0; // To store the amount collected
while (sold < N && q.peek() > 0)
{
ans = ans + q.peek(); //update the collected amount
int temp = q.peek();
q.poll();
q.add(temp - 1); //decrement and insert
sold++; //increment sold
}
return ans;
}
Odd even level difference
Given a binary tree , we have to compute the difference between sum of nodes at odd and even level.
Example -
Input:
2
/ \
4 8
Output: -10(2-(4+8))
Approach:
We can use level order traversal of tree to compute this.Initialise two variables for storing odd and even sums. On traversing through each level , we check if it's odd or even and update even or odd sum accordingly.
Time Complexity: O(N), where N is the number of levels.
Solution -
static int dif(Node node)
{
if (node == null)
return 0;
Queue<Node> q = new LinkedList<>();//for level order traversal
q.add(node);
int l = 0; //level
int e = 0, o = 0; //even and odd sum
while (q.size() != 0) //till queue is not empty
{
int s = q.size();
l++;
while (s > 0) {
Node temp = q.remove();
if (l % 2 == 0)
{
e += temp.data; //even level
}
else
{
o += temp.data; //odd level
}
if (temp.left != null)
{
q.add(temp.left); //left child
}
if (temp.right != null)
{
q.add(temp.right); //right child
}
s--;
}
}
return (o - e);
}
To-Do-
The snake game available in nokia games serves as the perfect example where queues can be used.
Thegame starts with the snake kept at (0,0) with size = 1 unit.A list of food's positions is given to you. As the snake eats his food, he grows in size by 1 unit.Each food appears one by one on the screen.On eating one food, score gets incremented by 1 unit.
Try implementing this yourself!
Hint
We can use a queue to track the snake positions.
With this article at OpenGenus, you must be having a clear idea of cases where queues serve to be of great importance , so go ahead and use it in your programs. Happy Coding!
