Egg Dropping Puzzle

In this article, we have explored the Egg Dropping Puzzle in depth with various algorithms including Combinatorics and Dynamic Programming.

Table of contents

I. Introduction into the problem
II. 2 eggs k floors
III. N eggs k floors
3.1 using combinatorics
3.1.1 top-down approach
3.1.2 bottom-up approach
3.2 using Dynamic programming
3.2.1 top-down approach
3.2.2 bottom-up approach

I. Introduction into the problem

The Egg Dropping Puzzle represents a problem to find the best method to test dropping eggs from a certain floor with as few resources and attempts possible.

In reality the eggs are very fragile, so dropping it from your hands it becomes very nasty :)

So, how will you try to test dropping 1 egg from 10 floors, or 2 eggs from 100 floors, or N eggs from k floors ?

In the first case you can try it by dropping it from the first floor and continue to the 10th one. That will be a linear approach with O(n) complexity.
How about trying it firstly from the 5th floor and if it breaks then you would know for sure it will break if you drop it from the above floors but you will not know from which inferior floor will be safe to drop because you don't have any other eggs to test.
If it doesn't break then you can continue with the 7th floor, meaning the half way of the untested floors, and so on.
You can realize that with 1 egg this approach of testing is not a good way, so you might think to add another egg.

II. 2 eggs k floors

With 2 eggs you can try the previous strategy, but again, at some point it might break again and you don't have other eggs to test with, especially if the numbers of floors will increase to 100 !
What if will change the strategy and start dropping the first egg from a specified floor in such away that if it breaks, the second egg will cover all the untested floors behind it ?
In this case, if the first egg breaks at the k floor, you will have the second chance with the second egg to check for the k-1 remaining floors, having a total number of attempts of (x-1)+1 which means x, where x-1 is the egg that dropped from the k-1 floor after the previous attempts had been done safely and 1 is the attempt from the k floor.

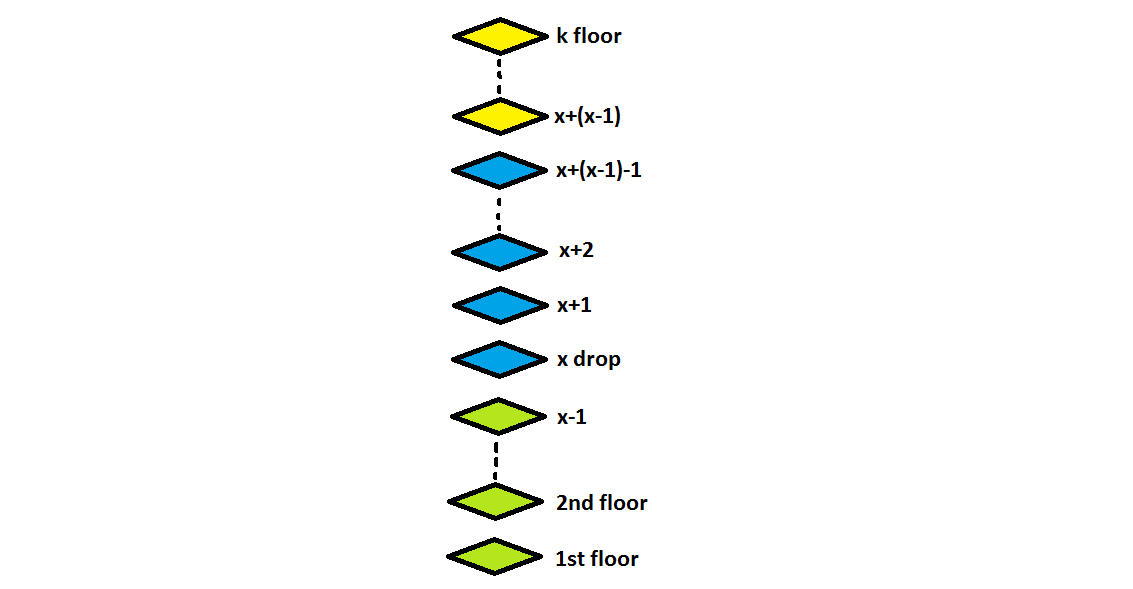
This will lead us to cover at any time a fix number of floors that can be translated mathematically by the next formula:

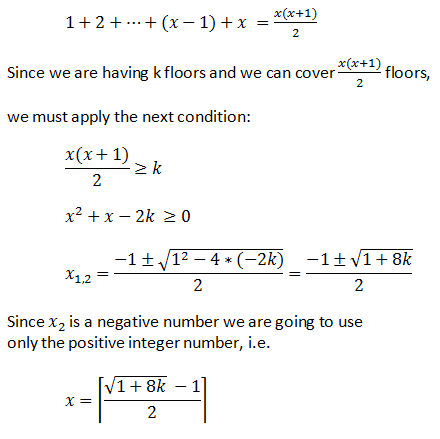
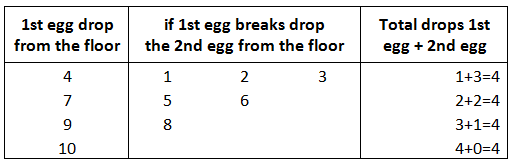
In case of 10 floors, x = 4 drops

In case of 100 floors, x = 13.65 = 14 drops

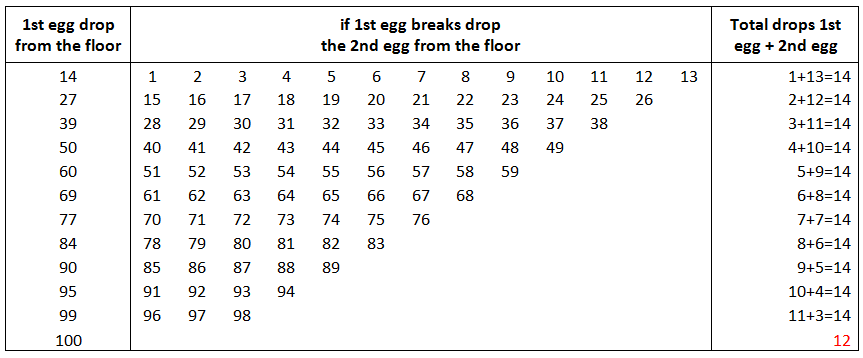
Notice the total number of attempts of the first egg, which is less than 14, and thus because the x mod 2 was different than 0 !

The above logic can be translated into the next C++ program:

    #include <iostream>
    #include <math.h>

    using namespace std;

    int main()
    {
        int i=0,j=0,l=1;
        int k=108;
        double f=(sqrt(8*k+1)-1) / 2.0;
        int x = (int)(f+0.9); //round up the number of floors

        for (i=x; i<=k && l<=x; i+=x-l++ )
            {
                cout<<i<<endl;
                for (j=i-(x-l); j<i; j++)
                    cout<<" "<<j;
                cout<<endl;
            }
        //next for is used to cover the untested floors for the 1st egg    
        for (i=i-(x-l); i<=k; i++ )
            cout<<i<<endl;
        return 0;
    }

Output for k=108:

    15
     1 2 3 4 5 6 7 8 9 10 11 12 13 14
    29
     16 17 18 19 20 21 22 23 24 25 26 27 28
    42
     30 31 32 33 34 35 36 37 38 39 40 41
    54
     43 44 45 46 47 48 49 50 51 52 53
    65
     55 56 57 58 59 60 61 62 63 64
    75
     66 67 68 69 70 71 72 73 74
    84
     76 77 78 79 80 81 82 83
    92
     85 86 87 88 89 90 91
    99
     93 94 95 96 97 98
    105
     100 101 102 103 104
    106
    107
    108

III. N eggs k floors

3.1 using combinatorics

The above solution can be written using combinatorics and extended to the general case.

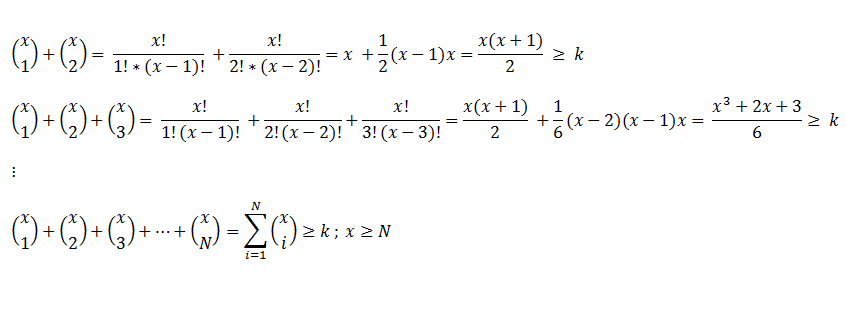
If number of eggs N is greater than number of attemps x then a condition of minimality needs to be added.

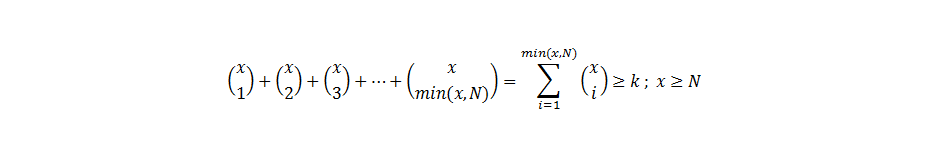
Quite complicate when you see all these equations, but in fact this will be easily to implement when programming if we are going to apply the recursion property of combinations.

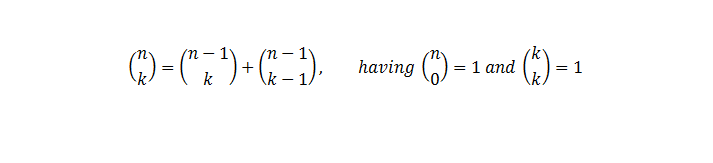
Basically what will need to do is to determine the first x, or minimum number of attemps, when sum of combinations is greather or equal with the number of floors.

We can use either linear search or a binary search algorithm to find the x.
The difference will be in time execution which:

• in case of linear search is O(n)
• in case of binary search is O(log n)

On these algorithms will add the time execution for the combinations determination which

• in case of comb function is O(2^n)
• in case of sum_comb function is O(n)

    #include <iostream>
    #include <bits/stdc++.h>
    #include <chrono>

    using namespace std;

    int comb (int attemps, int eggs)
    {
      if (eggs == 0 || attemps == eggs)
        return 1;
      return comb (attemps - 1, eggs) + comb (attemps - 1, eggs - 1);
    }

    int sum_comb (int attemps, int eggs)
    {
      long long unsigned int sum = 0;
      
      if(attemps < eggs) eggs = attemps;

      for (int i = 1; i <= eggs; i++)
        sum += comb (attemps, i);

      return sum;
    }

    int linear_search (int eggs, int floors)
    {
      int attemps, sum=0, i = 1;

      while ( sum < floors)  
        {
            sum = sum_comb(i,eggs);
            attemps = i++;
        };

      return attemps;
    }
    
    int binary_search (int eggs, int floors)
    { int sum ;
      int limit_inf = 1;
      int limit_sup = floors;
      int mid ;

      while (limit_inf <= limit_sup)
        {
            mid = (limit_inf + limit_sup) / 2.0;
            sum = sum_comb(mid,eggs);
            if(sum < floors)
                limit_inf = mid + 1;
            else if(sum > floors) 
                    limit_sup = mid - 1;
                 else
                    return mid;
        }
        return mid;
    }
    int main ()
    {
      double time_taken;
      
      int N=2, k=100;  
      
      auto start = chrono::high_resolution_clock::now();
      ios_base::sync_with_stdio(false);
      cout <<"linear search: "<< linear_search (N, k)<<endl;
      auto end = chrono::high_resolution_clock::now();
      time_taken = chrono::duration_cast<chrono::nanoseconds>(end - start).count();
      time_taken *= 1e-9;
      cout << "Time taken by linear search is : " << fixed 
             << time_taken << setprecision(6)<< " sec" << endl;
      
      start = chrono::high_resolution_clock::now();
      ios_base::sync_with_stdio(false);
      cout <<"binary search: "<< binary_search (N, k)<<endl;
      end = chrono::high_resolution_clock::now();
      time_taken = chrono::duration_cast<chrono::nanoseconds>(end - start).count();
      time_taken *= 1e-9;
      cout << "Time taken by binary search is : " << fixed 
             << time_taken << setprecision(6)<< " sec" << endl;
      
      return 0;
    }

Output:

linear search: 14
Time taken by linear search is : 0.000065 sec
binary search: 14
Time taken by binary search is : 0.000025 sec

3.1.1 top-down approach

We saw earlier how to generate solution using recursion definition of combinations.
Could we improve the previous program ?

The binary search is optimized, the sum of combinations is simply a sum, so the only code that remains to be improved is the comb function.
Since we are calculating using recoursion property of them, the multiple calls of the function will result in calling the same function multiple times for the same result.
The next example is ilustrating that:

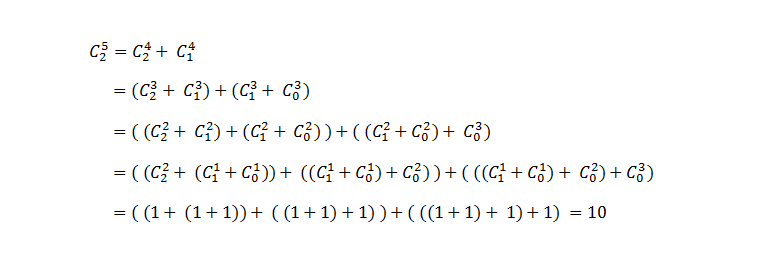
Can we improve that ?

How about saving the previous results once they are called and only reference the value in other calls ? This technique is called memoization, meaning we first split the problem in sub-problems and then calculate and store the results.

Note: Since we are starting with 1 and for simplicity of learning, the first column in the matrix is not used.

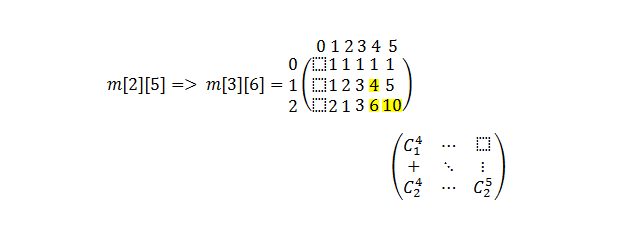
    #include <iostream>
    #include <bits/stdc++.h>
    #include <chrono>

    using namespace std;

    int **m;

    void init (int N, int k)
    {
        int i;

        //dynamically memory allocation
        m = new int* [N+1];
        for (i=0;i<k+1;i++)
            m[i] = new int[k+1]; 

        //matrix initialization
        for (i=1; i<= k; i++)
            {
                m[0][i] = 1;
                if (i<=N) m[i][i] = 1;
            }
    }

    int comb_memoization (int N, int k)
    {
        if (m[N][k] != 1)
            m[N][k] = comb_memoization(N-1,k-1) + comb_memoization(N,k-1) ;

        return m[N][k];                        
    }

    int sum_comb (int attemps, int eggs)
    {
      int sum = 0;

      if(attemps < eggs) eggs = attemps;

      for (int i = 1; i <= eggs; i++)
        sum += comb_memoization (i, attemps);

      return sum;
    }

    int linear_search (int eggs, int floors)
    {
      int attemps, sum=0, i = 1;

      while ( sum < floors)  
        {
            sum = sum_comb(i,eggs);
            attemps = i++;
        };

      return attemps;
    }

    int binary_search (int eggs, int floors)
    { int sum ;
      int limit_inf = 1;
      int limit_sup = floors;
      int mid ;

      while (limit_inf <= limit_sup)
        {
            mid = (limit_inf + limit_sup) / 2.0;
            sum = sum_comb(mid,eggs);
            if(sum < floors)
                limit_inf = mid + 1;
            else if(sum > floors) 
                    limit_sup = mid - 1;
                 else
                    return mid;
        }
        return mid;
    }
    int main ()
    {

      double time_taken;

      int N=2, k=100;  

      init(N,k);

      auto start = chrono::high_resolution_clock::now();
      ios_base::sync_with_stdio(false);
      cout <<"linear search: "<< linear_search (N, k)<<endl;
      auto end = chrono::high_resolution_clock::now();
      time_taken = chrono::duration_cast<chrono::nanoseconds>(end - start).count();
      time_taken *= 1e-9;
      cout << "Time taken by linear search is : " << fixed 
             << time_taken << setprecision(6)<< " sec" << endl;

      start = chrono::high_resolution_clock::now();
      ios_base::sync_with_stdio(false);
      cout <<"binary search: "<< binary_search (N, k)<<endl;
      end = chrono::high_resolution_clock::now();
      time_taken = chrono::duration_cast<chrono::nanoseconds>(end - start).count();
      time_taken *= 1e-9;
      cout << "Time taken by binary search is : " << fixed 
             << time_taken << setprecision(6)<< " sec" << endl;

      return 0;
    }

Output:

linear search: 14
Time taken by linear search is : 0.000055 sec
binary search: 14
Time taken by binary search is : 0.000032 sec

3.1.2 bottom-up approach

The top-down approach to calculate combinations using the recursion formula it takes a little bit more time to get the result. We might then think to use the factorial formula to calculate combinations but in this case there will be many multiplications to calculate for it.

How about using the Pascal triangle logic to calculate the combinations from bottom-up without using recursion ? In this way, we are getting used of the recursion definition of the combinations but without implementing in programming.
This technique is called tabulation.

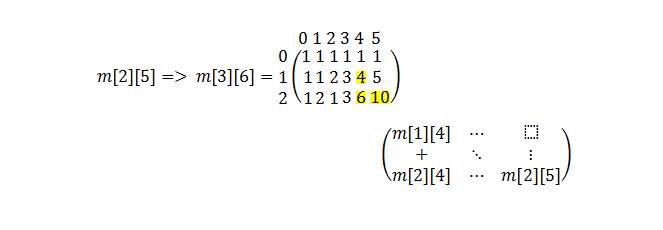
This will give us an execution time of O(n^2)

The next code is doing so:

    #include <iostream>
    #include <bits/stdc++.h>
    #include <chrono>

    using namespace std;

    int **m;

    void init (int N, int k)
    {
        int i;
        
        //dynamically memory allocation
        m = new int* [N+1];
        for (i=0;i<k+1;i++)
            m[i] = new int[k+1]; 
        
        //matrix initialization
        for(int i=0; i<=N; i++)
            for (int j=0; j<=k; j++)
            {
                m[i][j] = 0;
                m[0][j] = 1;
                m[i][0] = 1;
                m[i][i] = 1;
            }
    }
    
    int comb_tabulation (int N, int k)
    {
        for(int i=1; i<=N; i++)
            for (int j=1; j<=k; j++)
                {
                if (m[i][j] != 1)
                    m[i][j] = m[i-1][j-1] + m[i][j-1] ;
               }
    return m[N][k];                        
    }
    
    int sum_comb (int attemps, int eggs)
    {
      long long unsigned int sum = 0;
      
      if(attemps < eggs) eggs = attemps;

      for (int i = 1; i <= eggs; i++)
        sum += comb_tabulation (i, attemps);

      return sum;
    }

    int linear_search (int eggs, int floors)
    {
      int attemps, sum=0, i = 1;

      while ( sum < floors)  
        {
            sum = sum_comb(i,eggs);
            attemps = i++;
        };

      return attemps;
    }
    
    int binary_search (int eggs, int floors)
    { int sum ;
      int limit_inf = 1;
      int limit_sup = floors;
      int mid ;

      while (limit_inf <= limit_sup)
        {
            mid = (limit_inf + limit_sup) / 2.0;
            sum = sum_comb(mid,eggs);
            if(sum < floors)
                limit_inf = mid + 1;
            else if(sum > floors) 
                    limit_sup = mid - 1;
                 else
                    return mid;
        }
        return mid;
    }
    
    int main ()
    {
      double time_taken;
      
      int N=2, k=100;  
      
      init(N,k);
      
      auto start = chrono::high_resolution_clock::now();
      ios_base::sync_with_stdio(false);
      cout <<"linear search: "<< linear_search (N, k)<<endl;
      auto end = chrono::high_resolution_clock::now();
      time_taken = chrono::duration_cast<chrono::nanoseconds>(end - start).count();
      time_taken *= 1e-9;
      cout << "Time taken by linear search is : " << fixed 
             << time_taken << setprecision(6)<< " sec" << endl;
      
      start = chrono::high_resolution_clock::now();
      ios_base::sync_with_stdio(false);
      cout <<"binary search: "<< binary_search (N, k)<<endl;
      end = chrono::high_resolution_clock::now();
      time_taken = chrono::duration_cast<chrono::nanoseconds>(end - start).count();
      time_taken *= 1e-9;
      cout << "Time taken by binary search is : " << fixed 
             << time_taken << setprecision(6)<< " sec" << endl;
      
      return 0;
    }

Output:

linear search: 14
Time taken by linear search is : 0.000052 sec
binary search: 14
Time taken by binary search is : 0.000004 sec

3.2 using Dynamic programming

In short terms Dynamic programming refers to determine a functional equation that our problem will move forward from an incipient state of the solution to the optimal one.

Lets name s(n,p) the pair of the n'th remained egg to be tested and p'th remained floor untested, where:
n = 0,1,2,..., N-1
p = 0,1,2,..., k-1

The initial state of the process is s = (N,k) where N denotes the number of test eggs available at the commencement of the experiment. The process terminates either when there are no more test eggs (n = 0) or when p = 0, whichever occurs first. If termination occurs at state s = (0,p) and p > 0, then the test failed.

Now, let W(n,p) = minimum number of trials required to identify the value of the critical floor under the worst-case scenario given that the process is in state s = (n,p). (1)

Then, it can be shown that:

W(n,p) = 1 + min{ max( W(n−1, x−1), W(n, p−x) ); x = 1,2,...,p }

having W(n,0) = 0 for all n > 0 and W(1,p) = p for all p > 0 (2) (3)

Example for w(2,5)=3

Notice the execution number of times for each colour.

This will give us an execution time of O(2^n)

The next code will do so, but it will be very slowly:

    #include <iostream>
    #include <limits.h>
    #include <bits/stdc++.h>
    #include <chrono>

    using namespace std;

    int w(int n, int p)
    {
        if (p==0)  return 0;
        if (n==1)  return p;

        int minimum=INT_MAX;

        for (int x = 1; x<=p; x++)
            minimum = min(minimum, max(w(n-1,x-1), w(n,p-x))) ; 

        return 1 + minimum;
    }

    int main()
    {
      double time_taken;
      
      int N=2, k=100;  
      
      auto start = chrono::high_resolution_clock::now();
      ios_base::sync_with_stdio(false);
      cout <<"DP top-down: "<< w (N, k)<<endl;
      auto end = chrono::high_resolution_clock::now();
      time_taken = chrono::duration_cast<chrono::nanoseconds>(end - start).count();
      time_taken *= 1e-9;
      cout << "Time taken by DP top-down is : " << fixed 
             << time_taken << setprecision(6)<< " sec" << endl;

        return 0;
    }

Output:

Killed

Note: As you could see from the output, our test compiler killed the process because of long time execution. You might run it with another parameter w(2,10) to see the output of it or if you wish to run it locally you might have a chance to take a nap before you will get a result.

3.2.1 top-down approach

To improve the DP recursion we might invoke again the memoization technique by storing the calculated values in a matrix form.

The next program will do so:

    #include <iostream>
    #include <limits.h>
    #include <bits/stdc++.h>
    #include <chrono>

    using namespace std;

    int **m;

    void init (int N, int k)
    {
        int i,j;

        //dynamically memory allocation
        m = new int* [N+1];
        for (i=0;i<k+1;i++)
            m[i] = new int[k+1]; 

        //matrix initialization
        for(int i=0; i<=N; i++)
            for (int j=0; j<=k; j++)
            {
                m[i][j] = INT_MAX;
                m[i][0] = 0;
                m[1][j] = j;
            }
    }
    
    int w(int n, int p)
    {
        /*
        // v1 testing condition
        if (p == 0 ) return m[n][p];
        if (n == 1 ) return m[n][p];
        if (m[n][p] != INT_MAX) return m[n][p];
        
        // v2 testing condition
        if (m[n][p] == 0 || m[n][p] == 1 || m[n][p] != INT_MAX) return m[n][p];
        */
        
        // v3 testing condition
        if (p == 0 || n == 1 || m[n][p] != INT_MAX) return m[n][p];

        for (int x = 1; x<=p; x++)
            m[n][p] = min(m[n][p], max(w(n-1,x-1), w(n,p-x))) ;
        
        m[n][p] = m[n][p] + 1;    
        
        return m[n][p];
    }

    int main()
    {
      double time_taken;
      
      int N=2, k=100;  
      
      init(N,k);
      
      auto start = chrono::high_resolution_clock::now();
      ios_base::sync_with_stdio(false);
      cout <<"DP top-down: "<< w (N, k)<<endl;
      auto end = chrono::high_resolution_clock::now();
      time_taken = chrono::duration_cast<chrono::nanoseconds>(end - start).count();
      time_taken *= 1e-9;
      cout << "Time taken by DP top-down is : " << fixed 
             << time_taken << setprecision(6)<< " sec" << endl;

        return 0;
    }

Output:

DP top-down: 14
Time taken by DP top-down is : 0.000190 sec

Notice the incrementation of the cell m[n][k] before returning the value.

Also, which version (1,2 or 3) of the testing conditions do you think will be fast ? , not that it would matter somehow.

3.2.2 bottom-up approach

Since the previous approach is very slow, maybe we can improve it.
Again, using an aditional array to store the previous results, will be a good technique.
The problem will be: how to translate the functional equation into a matrix determination ?
Because we would not call the function in a recursive way, the incrementation needs to be done prior assigment.

m[n][p] = min{ 1 + max( m[n−1][ x−1], m[n][p−x] ); x = 1,2,...,p }

having:
m[n][0] = 0 for all n > 0
m[1][p] = p for all p > 0
m[0][p] = 0 for all p > 0
m[n][1] = 1 for all n > 0

Example for w(2,5)=3

This will give us an execution time of O(n^3)

The next code will do so:

    #include <iostream>
    #include <limits.h>
    #include <bits/stdc++.h>
    #include <chrono>

    using namespace std;

    int **m;

    void init (int N, int k)
    {
        int i,j;

        //dynamically memory allocation
        m = new int* [N+1];
        for (i=0;i<k+1;i++)
            m[i] = new int[k+1]; 

        //matrix initialization
        for(int i=0; i<=N; i++)
            for (int j=0; j<=k; j++)
            {
                m[i][j] = INT_MAX;
                m[i][0] = 0;
                m[0][j] = 0;
                m[i][1] = 1;
                m[1][j] = j;
            }
    }

    void print (int N, int k)
    {

        for(int i=0; i<=N; i++)
            {
            for (int j=0; j<=k; j++)
                cout<<m[i][j]<<" ";
            cout<<endl;    
            }
    }
    int w (int N, int k)
    {
         for(int i=2; i<=N; i++)
            for (int j=1; j<=k; j++)
                for(int x=1; x<=j; x++)
                    m[i][j] = min( m[i][j], 1+ max( m[i-1][x-1], m[i][j-x] ));

        return m[N][k];                        
    }

    int main()
    {
      double time_taken;
      
      int N=2, k=100;  
      
      init(N,k);

      auto start = chrono::high_resolution_clock::now();
      ios_base::sync_with_stdio(false);
      cout <<"DP bottom-up: "<< w (N, k)<<endl;
      auto end = chrono::high_resolution_clock::now();
      time_taken = chrono::duration_cast<chrono::nanoseconds>(end - start).count();
      time_taken *= 1e-9;
      cout << "Time taken by DP bottom-up is : " << fixed 
             << time_taken << setprecision(6)<< " sec" << endl;

        return 0;
    }

Output:

DP bottom-up: 14
Time taken by DP bottom-up is : 0.000159 sec

Conclusion

Studing multiple ways to find a good algorithm to solve a problem might have a huge impact when appling into production.

From the above approaches we might notice that the best time solution is this case is the bottom-up combinatorics approach.